Моделирование случайных величин.

При моделировании дискретных случайных величин наиболее часто используются два метода:

· метод последовательных сравнёний;

· метод интерпретации.

Метод последовательных сравнений. Число r последовательно сравнивают со значением суммы 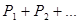, где Р ₁ вероятность наименьшего значения случайной величины Y, Р ₂ - вероятность второго величине значения. При первом выполнении следующего условия проверка прекращается и дискретная случайная величина Y считается принявшей значение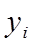

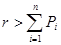
Процесс можно ускорить, применяя методы оптимизации перебора: дихотомии ранжирования Р и т. д. Величины Рi рассчитывают по функциям распределения вероятности, соответствующим моделируемому закону.

Метод интерпретации. Метод основан на физической трактовке моделируемого закона распределения. Например, биномиальное распределение описывает число успехов в n независимых испытаниях с вероятностью успеха в каждом испытании Р и вероятностью неудачи g =1- Р. При моделировании этого распределения с помощью метода интерпретации выбирают n независимых случайных чисел, равномерно распределенных на интервале [0, 1], и подсчитывают количество тех из них, которые меньше Р.

26. Стратегическое и тактическое планирование

Стратегическое планирование имитационного эксперимента.

Цель методов стратегического планирования имитационных экспериментов - получение максимального объема информации об исследуемой системе в каждом эксперименте (наблюдении). Другими словами, стратегическое планирование позволяет ответить на вопрос, при каком сочетании уровней внешних и внутренних факторов может быть получена наиболее полная и достоверная информация о поведении системы.

При стратегическом планировании эксперимента должны быть решены две основные задачи:

· идентификация факторов;

· выбор уровней факторов.

Под идентификацией факторов понимается их ранжирование по степени влияния на значение наблюдаемой переменной (показателя эффективности).

По итогам идентификации целесообразно разделить все факторы на две группы - первичные и вторичные. Первичные - это те факторы, в исследовании влияния которых экспериментатор заинтересован непосредственно. Вторичные – это факторы, которые не являются предметом исследования, но влиянием которых нельзя пренебречь.

Выбор уровней факторов производится с учетом двух противоречивых требований:

· уровни фактора должны перекрывать (заполнять) весь возможный диапазон его изменения;

· общее количество уровней по всем факторам не должно приводить к чрезмерному объему моделирования.

Отыскание компромиссного решения, удовлетворяющего этим требованиям, и является задачей стратегического планирования эксперимента.

Тактическое планирование эксперимента.

Совокупность методов установления необходимого объема испытаний относят к тактическому планированию экспериментов.

Поскольку точность оценок наблюдаемой переменной характеризуется ее дисперсией, то основу тактического планирования эксперимента составляют так называемые методы понижения дисперсии. В связи с этим для восприятия последующего материала читателю потребуются некоторые знания математической статистики.

В общем случае объем испытаний (величина выборки), необходимый для получения оценок наблюдаемой переменной с заданной точностью, зависит от следующих факторов:

· вида распределения наблюдаемой переменной у (напомним, при статистическом
эксперименте она является случайной величиной);

· коррелированности между собой элементов выборки;

· наличия и длительности переходного режима функционирования моделируемой системы.

27. Изменение шага с постоянным шагом и по особым состояниям

Изменение времени с постоянным шагом.

При использовании данного метода отсчет системного времени ведется через фиксированные, выбранные исследователем интервалы времени. События в модели считаются наступившими в момент окончания этого интервала. Погрешность в измерении временных характеристик системы в этом случаё зависит от величины шага моделирования .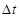

Метод постоянного шага целесообразно использовать в том случае, если:

· события появляются регулярно, и распределение во времени достаточно равномерно;

· число событий велико и моменты их появления близки;

· невозможно заранее определить моменты появления событий.

Данный метод управления модельным временем достаточно просто реализовать в
том случае, когда условия появления событий всех типов в модели можно представить как функцию времени.

Изменение времени по особым состояниям

При моделировании по особым состояниям системное время каждый раз изменяется на величину, строго соответствующую интервалу времени до момента наступления очередного события. В этом случае события обрабатываются в порядке их наступления, а одновременно наступившими считаются только те, которые являются одновременными в действительности.

Для реализации моделирования по особым состояниям требуется разработка специальной процедуры планирования событий (так называемого календаря событий). Если известен закон распределения интервалов между событиями, то такое прогнозирование труда не составляет: достаточно к текущему значению модельного времени добавить величину интервала, полученную с помощью соответствующего датчика.

Если же момент наступления события определяется некоторыми логическими условиями, то необходимо сформулировать эти условия и проверять их истинность для каждого последующего шага моделирования. Практика показывает, что сложности в реализации механизма изменения времени по особым состояниям связаны в первую очередь с корректным описанием таких условий. Трудности еще более возрастают, если в модели фигурируют несколько типов взаимосвязанных событий.

Моделирование по особым состояниям целесообразно использовать, если: события распределяются во времени неравномерно или интервалы между ними велики;

· предъявляются повышенные требования к точности определения взаимного положения событий во времени;

· необходимо учитывать наличие одновременных событий.

Дополнительное достоинство метода заключается в том; что он позволяет экономить машинное время, особенно при моделировании систем периодического действия в которых события длительное время могут не наступать.

28. Характеристики последовательных псевдо-случайных чисел

В основе всех методов и приемов моделирования случайных факторов лежит использование случайных чисел, имеющих равномерное распределение на интервале [0, 1]. «Истинно» случайные числа формируются с помощью аналого-цифровых преобразователей на основе сигналов физических генераторов, использующих естественные источники случайных шумов (радиоактивный распад, шумы электронных и проводниковых устройств и т. п.).

Случайные числа, генерируемые аппаратно или программно на ЭВМ, называются псевдослучайными. Однако их статистические свойства совпадают со статистическими свойствами «истинно» случайных чисел. В состав практически всех современных систем программирования входят специальные функции генерации случайных чисел, которые обычно называют датчиками или генераторами случайных чисел.

Наиболее простой метод программной генерации случайных чисел — мультипликативный; в его основе лежит следующее рекуррентное соотношение:

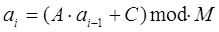
Здесь 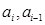- очередное и предыдущее случайные числа соответственно; А, С - константы; М - достаточно большое целое положительное число (чем больше М, тем
длиннее неповторяемая последовательность).

Достоинство метода заключается в том, что при одних и тех же значениях параметров, входящих в это выражение можно полностью воспроизвести эксперимент.

Рассмотрим методы проведения такого анализа, наиболее часто применяемые на практике.

1) Проверка равномерности. Проверка равномерности может быть выполнена с помощью гистограммы относительных частот генерируемой случайной величины.

2) Проверка стохастичности. Рассмотрим один из основных методов проверки - метод комбинаций. Выбирают достаточно большую последовательность случайных чисел х_i и для нее определяют вероятность появления в каждом из х_i ровно j. При этом могут анализироваться как все разряды числа, таки только l старших. Теоретически закон появления j единиц в l разрядах двоичного числа может быть описан как биноминальный закон распределения (исходя из независимости отдельных разрядов). Тогда при длине выборки N ожидаемое число появлений случайных чисел х_i с j единицами в проверяемых l разрядах будет равно:

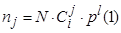
3) Проверка независимости. Проверка независимости проводится на основе вычисления корреляционного момента. Для оценки независимости элементов последовательности поступают следующим образом: 1. Вводят в рассмотрение дополнительную последовательность Y, в которой 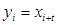где t - величина сдвига последовательности Y относительно исходной последовательности Х. 2. Вычисляют коэффициент корреляции случайных величин Х и Y, для чего используются специальные расчетные соотношения. Еще одна важная характеристика датчика случайных чисел - длина отрезка апериодичности L.

29. Моделирование случайных событий