
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
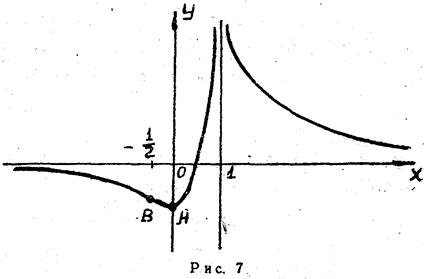
Задача 2. Исследовать функцию и построить ее график.
|
|
Исследовать функцию  и построить ее график.
и построить ее график.
Решение. Исследование функции проведем по следующей схеме:
- Найдем область определения функции.
- Исследуем функцию на непрерывность.
- Установим, является ли функция четной, нечетной.
- Найдем интервалы возрастания и убывания функции и точки экстремума.
- Найдем интервалы выпуклости и вогнутости кривой и точки ее перегиба.
- Найдем асимптоты кривой.
Реализуем указанную схему:
- Функция определена при всех значениях аргумента х, кроме
 .
.
2. Данная функция является элементарной, поэтому она непрерывна на своей области определения, т.е. на интервалах 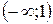 и
и 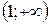 . В точке
. В точке  функция терпит разрыв второго рода.
функция терпит разрыв второго рода.
3. Для установления четности или нечетности функции проверим выполнимость равенств  (тогда
(тогда 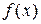 – четная функция) или
– четная функция) или  (для нечетной функции) для любых х и – х из области определения функции:
(для нечетной функции) для любых х и – х из области определения функции:
 .
.
Следовательно, 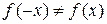 и
и  , то есть данная функция не является ни четной, ни нечетной.
, то есть данная функция не является ни четной, ни нечетной.
4. Для исследования функции на экстремум найдем ее первую производную:
 .
.
 при
при 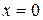 и
и  – не существует при
– не существует при  . Тем самым имеем две критические точки:
. Тем самым имеем две критические точки:  . Но точка
. Но точка  не принадлежит области определения функции, экстремума в ней быть не может.
не принадлежит области определения функции, экстремума в ней быть не может.
Разобьем числовую ось на три интервала (рис. 5): 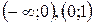 ,
, 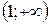 .
.
В первом и третьем интервалах первая производная отрицательна, следовательно, здесь функция убывает; во втором интервале – положительна и данная функция возрастает. При переходе через точку 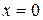 первая производная меняет свой знак с минуса на плюс, поэтому в этой точке функция имеет минимум:
первая производная меняет свой знак с минуса на плюс, поэтому в этой точке функция имеет минимум:  . Значит,
. Значит,  – точка минимума.
– точка минимума.
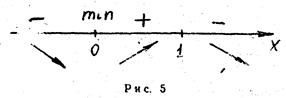
Нарис. 5 знаками +, – указаны интервалы знакопостоянства производной у', а стрелками – возрастание и убывание исследуемой функции.
5. Для определения точек перегиба графика функции и интервалов выпуклости и вогнутости кривой найдем вторую производную:
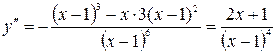 .
. 
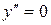 при
при  и
и 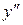 – не существует при
– не существует при  . Разобьем числовую ось на три интервала (рис. 6):
. Разобьем числовую ось на три интервала (рис. 6):  ,
, 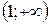 . На первом интервале вторая производная
. На первом интервале вторая производная 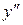 отрицательна и дуга исследуемой кривой выпукла; на втором и третьем интервалах
отрицательна и дуга исследуемой кривой выпукла; на втором и третьем интервалах 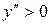 , тем самым график является вогнутым. При переходе через точку
, тем самым график является вогнутым. При переходе через точку 
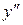 меняет свой знак, поэтому
меняет свой знак, поэтому  – абсцисса точки перегиба.
– абсцисса точки перегиба.
Следовательно,  – точка перегиба графика функции.
– точка перегиба графика функции.

6.  – точка разрыва функции, причем
– точка разрыва функции, причем  . Поэтому прямая
. Поэтому прямая  является вертикальной асимптотой графика. Для определения уравнения наклонной асимптоты
является вертикальной асимптотой графика. Для определения уравнения наклонной асимптоты  воспользуемся формулами:
воспользуемся формулами:
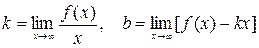 .
.
Тогда

При вычислении последнего предела использовалось правило Лопиталя. Значит прямая 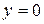 есть горизонтальная асимптота графика исследуемой функции, представленного на рис. 7.
есть горизонтальная асимптота графика исследуемой функции, представленного на рис. 7.
|
|