
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача 1. Найти производные функций.
|
|
Найти производные функций.
1. а) 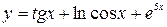 ; б)
; б) 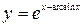 ;
;
в) 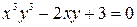 .
.
2. а) 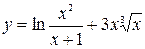 ; б)
; б) 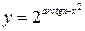 ;
;
в) 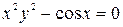 .
.
3. а) 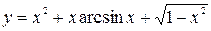 ; б)
; б) 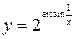 ;
;
в) 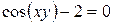 .
.
4. а) 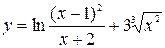 ; б)
; б) 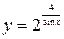 ;
;
в) 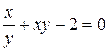 .
.
5. а) 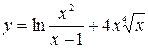 ; б)
; б) 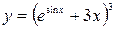 ;
;
в)  .
.
6. а) 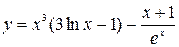 ; б)
; б) 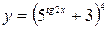 ;
;
в) 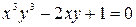 .
.
7. а) 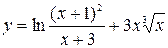 ; б)
; б) 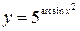 ;
;
в) 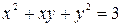 .
.
8. а) 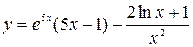 ; б)
; б) 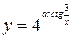 ;
;
в) 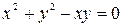 .
.
9. а) 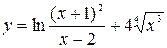 ; б)
; б) 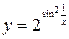 ;
;
в) 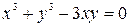 .
.
10. а) 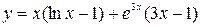 ; б)
; б) 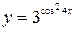 ;
;
в) 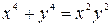 .
.
Задача 2.
Исследовать данные функции методами дифференциального исчисления и построить их графики. Исследование функции рекомендуется проводить по следующей схеме: 1) найти область определения функции; 2) исследовать функцию на непрерывность; 3) определить, является ли данная функция четной, нечетной; 4) найти интервалы возрастания и убывания функции и точки ее экстремума; 5) найти интервалы выпуклости и вогнутости графика функции и точки перегиба; 6) найти асимптоты графика функции.
1. 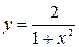 . 2.
. 2. 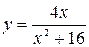 . 3.
. 3. 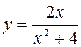 .
.
4. 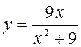 . 5.
. 5. 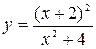 . 6.
. 6. 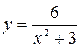 .
.
7. 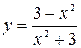 . 8.
. 8. 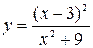 . 9.
. 9. 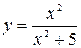 .
.
10. 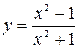 .
.
Задание 3.
Найти указанные неопределенные интегралы и результаты интегрирования проверить дифференцированием.
1. а) 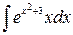 ; б)
; б) 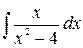 ; в)
; в) 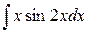 .
.
2. а) 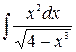 ; б)
; б) 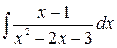 ; в)
; в) 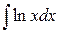 .
.
3. а) 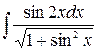 ; б)
; б) 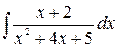 ; в)
; в) 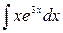 .
.
4. а) 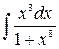 ; б)
; б) 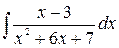 ; в)
; в)  .
.
5. а) 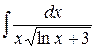 ; б)
; б) 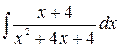 ; в)
; в) 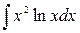 .
.
6. а) 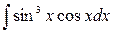 ; б)
; б) 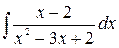 ; в)
; в) 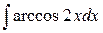 .
.
7. а) 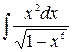 ; б)
; б)  ; в)
; в) 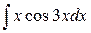 .
.
8. а) 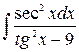 ; б)
; б) 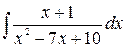 ; в)
; в)  .
.
9. а) 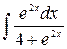 ; б)
; б) 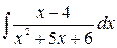 ; в)
; в) 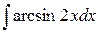 .
.
10. а) 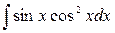 ; б)
; б) 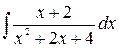 ; в)
; в) 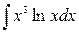 .
.
|
|