
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Электродинамика и распространение радиоволн 4 страница
|
|
Получив у преподавателя допуск, приступить к выполнению лабораторной работы в следующем порядке:
1. Подготовить генератор к работе.
2. Включить приборы в сеть, после прогрева (10− 15 мин) ручками «Подстройка» и «Регулировка выхода ВЧ» добиться максимального уровня отклонения стрелочного индикатора. Частота генерации при этом должна быть не более 1100 МГц.
3. Установить приемную антенну (вибратор Пистолькорса) по центру щелевой антенны.
4. Произвести согласование антенн по поляризации, вращая экран щелевой антенны и поворачивая шлейф приемного вибратора вокруг оси. Приемную антенну следует установить параллельно вектору напряженности электрического поля, излучаемого щелевой антенной.
5. Снять диаграмму направленности щелевой антенны в азимутальной плоскости (в 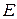 -плоскости), перемещая приемный вибратор с помощью поворотного устройства в пределах от 0˚ до 180˚ через каждые 10˚. Для каждого положения приемной антенны записать соответствующее показание индикатора.
-плоскости), перемещая приемный вибратор с помощью поворотного устройства в пределах от 0˚ до 180˚ через каждые 10˚. Для каждого положения приемной антенны записать соответствующее показание индикатора.
6. Установить щелевую антенну в горизонтальное положение, произвести согласование с приемной антенной по поляризации и снять диаграмму направленности в меридиональной плоскости (в Н -плоскости) щелевой антенны.
Содержание отчета
1. Схема измерительной установки.
2. Таблицы полученных измерений тока на вибраторе Пистолькорса в зависимости от его углового положения относительно щели.
3. Полученные диаграммы направленности в меридиональной и азимутальной плоскостях, построенные в полярной системе координат.
4. Краткая сводка результатов всех проведенных измерений и расчетов.
5. Выводы по полученным результатам.
Контрольные вопросы
1. Почему щелевую антенну можно рассматривать как фиктивную элементарную магнитную антенну?
2. Нарисовать плоскую проводящую рамку (одиночный виток провода), эквивалентный ей фиктивный магнитный излучатель и поля, создаваемые этими элементарными антеннами.
3. Что такое векторный потенциал, чем определяется его величина и как он направлен в точке наблюдения по отношению к оси антенны?
4. Основные параметры щелевого излучателя, как они связаны с λ и l?
5. Диаграмма направленности элементарной щелевой антенны, ее отличие от ДН элементарного электрического излучателя.
6. Излучающие и неизлучающие щели в волноводах.
7. Чем характеризуются ближняя, промежуточная и дальняя зоны? Каков характер комплексного вектора Пойнтинга в этих зонах?
8. В чем заключается принцип перестановочной двойственности?
9. Переход от элементарной магнитной антенны к щелевой.
Граничные условия на поверхности пластины и за ее пределами.
10. Показать направление токов смещения в щелевой антенне.
11. Поляризация излучения щелевой антенны.
12. Направления максимального и минимального излучения элементарной магнитной антенны.
Лабораторная работа № 5
ИССЛЕДОВАНИЕ ПОПЕРЕЧНО-НАМАГНИЧЕННОГО ФЕРРИТА
Цель работы: Ознакомление с явлениями в поперечно-намагниченном феррите, связанными с его невзаимными свойствами; экспериментальное определение зависимостей невзаимных свойств феррита от величины подмагничивающего поля.
Применение ферритовых вентилей в технике СВЧ
Во многих видах трактов СВЧ предъявляются высокие требования
к согласованию источника СВЧ мощности с нагрузкой, поскольку генераторы весьма чувствительны к влиянию отраженной волны. Решить задачу качественного согласования в полосе частот (до 30 − 40 %) обычными методами
(с помощью реактивных согласующих устройств) достаточно сложно, а при переменной нагрузке вообще невозможно. Такая задача легко решается при включении между генератором и нагрузкой магнитных вентилей (циркуляторов), работа которых основана на невзаимных свойствах ферритов по отношению к направлению распространения электромагнитных волн.
Вентилем называется двуплечее устройство (четырехполюсник), в котором падающая электромагнитная волна проходит без существенного затухания в одном направлении (прямая волна) и претерпевает сильное поглощение при распространении в противоположном направлении (обратная волна). Вентиль строится таким образом, чтобы затухание прямой волны было минимальным, а обратной – максимальным.
Качество работы вентиля характеризуется затуханиями прямой L пр и обратной L обр волн, которые измеряются в децибелах. Обычно вентиль конструируют и настраивают таким образом, чтобы величина L пр лежала в пределах 0.1 − 1.5 дБ, а L обр была не менее 10 дБ. В связи с этим, свойства вентиля характеризуются также вентильным отношением:
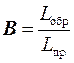 . (5.1)
. (5.1)
Обычно, рабочая полоса вентилей оценивается по уровню 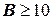 . Хотя в некоторых случаях эта величина может быть и больше. Все зависит от требований, диктуемых техническим заданием.
. Хотя в некоторых случаях эта величина может быть и больше. Все зависит от требований, диктуемых техническим заданием.
Строение ферритов
Известно, что все атомы всех веществ состоят из положительно заряженных ядер и отрицательно заряженных электронов. Общее число электронов в атоме равно номеру элемента в периодической системе Менделеева. Условно можно считать, что каждый электрон вращается по некоторой орбите вокруг ядра, одновременно вращаясь вокруг собственной оси.

Рис. 5.1. Поле рамки с током.
Поскольку электрон – заряженная частица, а перемещение заряженных частиц по замкнутой траектории эквивалентно протеканию тока в контуре, то орбиту каждого электрона можно рассматривать как элементарный виток с током (рис. 5.1).
Ток создает в окружающем пространстве магнитное поле, перпендикулярное плоскости рамки, которое характеризуется орбитальным магнитным моментом 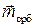 (рис. 5.2). Вращению электрона вокруг собственной оси соответствует спиновый магнитный момент
(рис. 5.2). Вращению электрона вокруг собственной оси соответствует спиновый магнитный момент 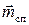 .
.
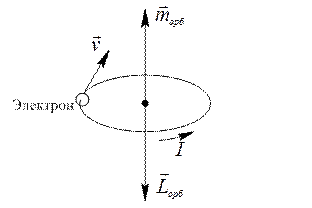
Рис. 5.2. Орбитальный момент электрона.
Вращающийся электрон со своей массой может быть уподоблен волчку, одновременно вращающемуся вокруг собственной оси и ядра. Следовательно, электрон как материальная точка имеет орбитальный 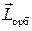 и спиновый
и спиновый 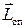 моменты количества движения (рис. 5.2 и 5.3 соответственно).
моменты количества движения (рис. 5.2 и 5.3 соответственно).
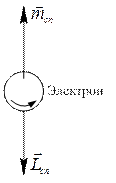
Рис. 5.3. Спиновый момент электрона.
Полный магнитный и механический моменты атома – векторные суммы моментов всех электронов в атоме. В свою очередь, полные моменты молекул – суммы моментов атомов в молекуле и т. д.
При анализе состояний электронов в атомах и молекулах следует опираться на фундаментальный физический принцип, согласно которому произвольная физическая система находится в устойчивом во времени состоянии, если ее полная энергия минимальна.
У большинства атомов минимум полной энергии достигается при антипараллельной ориентации спиновых моментов, т. е. суммарный магнитный момент этих атомов близок к нулю. Исключение составляют металлы переходных групп (группы железа, палладия, платины и т. д.), у которых минимуму полной энергии соответствует параллельная ориентация спиновых магнитных и механических моментов части электрона. Например, у атома железа на предпоследней оболочке находятся четыре электрона с параллельными спинами, у атома кобальта – три и т. д.
В постоянном магнитном поле атомы этих металлов ведут себя подобно стрелке компаса; их магнитные моменты ориентируются параллельно приложенному магнитному полю.
Принцип действия ферритовых устройств на СВЧ основан на взаимодействии магнитного поля электромагнитной волны с нескомпенсированными магнитными моментами атомов. Чтобы такое взаимодействие стало возможным, электромагнитная волна должна проникать в вещество и распространяться в нем. В проводниках распространение волн невозможно из-за скин-эффекта, поэтому чистое железо непригодно для использования в подобных устройствах. Это препятствие устраняется при применении диэлектрических магнитных материалов, являющихся химическими соединениями магнитных металлов (обычно железа) с кислородом и другими элементами. Подобные магнитные диэлектрики, называемые ферритами, имеют весьма малую удельную проводимость порядка 10-4...10-6 См/м, в то время как железо в диапазоне СВЧ имеет проводимость 106 См/м. Диэлектрическая проницаемость ферритов на СВЧ, как правило, попадает в интервал 5− 20.
Химическая формула простейших ферритов имеет вид 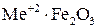 , где
, где 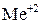 − ион двухвалентного металла типа Mn, Co, Ni, Cu, Mg, Zn, Cd и др. Часто используют смешанные ферриты, в состав которых входят ионы нескольких металлов.
− ион двухвалентного металла типа Mn, Co, Ni, Cu, Mg, Zn, Cd и др. Часто используют смешанные ферриты, в состав которых входят ионы нескольких металлов.
Ферриты отличаются от других магнитных материалов тем, что они, как и ферромагнетики, состоят из большого числа малых однородно намагниченных областей – доменов. Внутри каждого домена намагниченность однородна, но направление вектора магнитного момента в этих самопроизвольно намагниченных областях изменяется от одного домена к другому. Поэтому при отсутствии внешнего магнитного поля феррит в целом не намагничен (рис. 5.4). Ширина домена 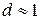 мкм. При внешнем магнитном поле
мкм. При внешнем магнитном поле 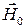 от
от
1 до 100 эрстед (102 − 104 А/м) доменная структура исчезает, и феррит намагничивается. В случае, когда все магнитные моменты в материале ориентированы по внешнему полю (образец намагничен до насыщения), магнитный момент единицы объема вещества называется намагниченностью насыщения. Конкретная величина поля насыщения зависит от марки феррита.
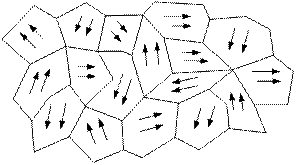
Рис. 5.4. Домены феррита в отсутствии внешнего магнитного поля.
Ферриты представляют собой ионные кристаллы, в которых сравнительно небольшие ионы металлов находятся в промежутках между значительно большими по размеру ионами кислорода О-2. В ионах кислорода отсутствуют непарные спиновые моменты, которые не обладают магнитным моментом. Взаимодействие между нескомпенсированными магнитными моментами ионов металлов может осуществляться только через ионы кислорода. Это приводит к параллельной или антипараллельной ориентации магнитных моментов ионов металлов в соседних ячейках кристаллической решетки. В состав ферритов входят ионы различных металлов, магнитные моменты которых не равны. Поэтому даже при антипараллельной ориентации имеет место неполная компенсация магнитных моментов. Следовательно, отдельные малые объемы материала оказываются намагниченными в одном направлении. Именно эти объемы и называются доменами. Из сказанного следует, что ферромагнетизм есть свойство кристалла, а не отдельного атома.
Технология изготовления ферритов подобна производству керамики. Порошкообразные исходные компоненты смешиваются со связующим материалом (например, парафином), прессуются и подвергаются обжигу в электропечах. Как уже указывалось, ферриты являются хорошими диэлектриками (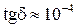 ), и поэтому потери на вихревые токи в них малы.
), и поэтому потери на вихревые токи в них малы.
Прецессия магнитного момента
Рассмотрим процессы, происходящие в намагниченном феррите. Физические явления в намагниченном феррите строго объясняются на уровне квантово-механических представлений.
Известно, что элементарным носителем магнитного момента является малый замкнутый плоский виток с током I (рис. 5.1), причем его магнитный момент равен:
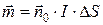 , (5.2)
, (5.2)
где 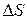 – площадь витка.
– площадь витка.
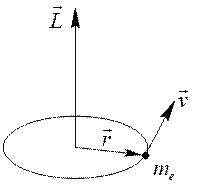
Рис. 5.5. Момент количества движения материальной точки.
С точки зрения механики электрон может быть уподоблен вращающейся материальной точке с массой me (рис. 5.5), момент количества движения которой равен:
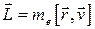 . (5.3)
. (5.3)
Если на вращающуюся материальную точку действует внешняя сила 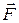 , то ее скорость изменяется в соответствии со вторым законом Ньютона:
, то ее скорость изменяется в соответствии со вторым законом Ньютона:
 . (5.4)
. (5.4)
Векторно умножим обе части уравнения (5.4) на 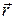 :
:
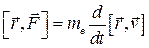 . (5.5)
. (5.5)
Слева имеем момент силы 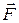 на плече
на плече 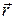 :
:
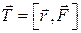 . (5.6)
. (5.6)
Отсюда с учетом (5.3) получается уравнение движения материальной точки, находящейся во вращательном движении:
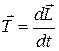 . (5.7)
. (5.7)

Рис. 5.6. Прецессия магнитного момента.
Квантовая механика устанавливает связь между спиновым магнитным моментом электрона и моментом количества движения:
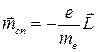 , (5.8)
, (5.8)
где 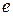 = 1, 6∙ 10-19 Кл − заряд электрона;
= 1, 6∙ 10-19 Кл − заряд электрона; 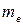 = 9, 11∙ 10-31 кг − масса электрона.
= 9, 11∙ 10-31 кг − масса электрона.
Если магнитный момент 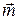 поместить в магнитное поле
поместить в магнитное поле 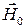 , то на него будет действовать пара сил, т. е. вращательный момент
, то на него будет действовать пара сил, т. е. вращательный момент 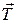 , который стремится повернуть момент электрона
, который стремится повернуть момент электрона 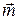 параллельно полю
параллельно полю 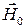 :
:
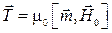 , (5.9)
, (5.9)
где 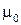 =
= 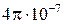 − магнитная постоянная.
− магнитная постоянная.
Наличие механического спинового момента делает электрон подобным гироскопу, ось которого под влиянием действующего на него момента 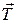 прецессирует (рис. 5.6).
прецессирует (рис. 5.6).
С учетом (5.8) подставим значение 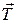 из (5.9) в уравнение (5.7), – получим уравнение движения магнитного момента:
из (5.9) в уравнение (5.7), – получим уравнение движения магнитного момента:
 . (5.10)
. (5.10)
Если в единице объема V вещества находится N нескомпенсированных магнитных моментов, то можно вести вектор намагниченности 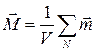 – магнитный момент в единице объема. Тогда из выражения (5.10) получим уравнение для неограниченной однородной среды:
– магнитный момент в единице объема. Тогда из выражения (5.10) получим уравнение для неограниченной однородной среды:
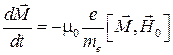 . (5.11)
. (5.11)
Обозначим 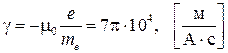 , где
, где 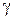 − гиромагнитное отношение. С учетом введенного обозначения перепишем (5.10):
− гиромагнитное отношение. С учетом введенного обозначения перепишем (5.10):
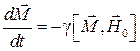 . (5.12)
. (5.12)
Это уравнение носит название уравнения движения намагниченности Ландау – Лифшица.
Намагниченность 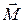 по смыслу является объемной плотностью нескомпенсированных магнитных моментов и определяется свойствами конкретной марки феррита.
по смыслу является объемной плотностью нескомпенсированных магнитных моментов и определяется свойствами конкретной марки феррита.
Векторное уравнение (5.12) эквивалентно трем скалярным уравнениям в декартовой системе координат:
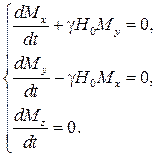 (5.13)
(5.13)
Здесь учтено, что в соответствии с рис. 5.6 поле 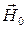 направлено вдоль оси OZ, т. е.
направлено вдоль оси OZ, т. е. 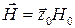 .
.
Решив совместно первые два уравнения из (5.13), получим:
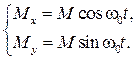 (5.14)
(5.14)
где 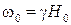 − частота свободной прецессии магнитного момента, гиромагнитная частота или частота ферромагнитного резонанса. Из (5.14) видно, что конец вектора
− частота свободной прецессии магнитного момента, гиромагнитная частота или частота ферромагнитного резонанса. Из (5.14) видно, что конец вектора 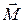 описывает окружность, вращаясь против часовой стрелки, если смотреть с конца вектора
описывает окружность, вращаясь против часовой стрелки, если смотреть с конца вектора 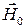 (правое вращение). При этом частота свободной прецессии определяется только величиной напряженности внешнего магнитного поля
(правое вращение). При этом частота свободной прецессии определяется только величиной напряженности внешнего магнитного поля 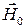 . В реальных ферромагнетиках из-за наличия потерь (магнитное трение) конец вектора
. В реальных ферромагнетиках из-за наличия потерь (магнитное трение) конец вектора 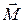 движется по скручивающейся спирали и через время порядка 10-8 с вектор
движется по скручивающейся спирали и через время порядка 10-8 с вектор 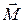 устанавливается параллельно вектору
устанавливается параллельно вектору 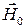 .
.
Из выражения 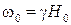 следует, что чем больше напряженность внешнего поля
следует, что чем больше напряженность внешнего поля 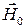 , тем выше частота прецессии. При реально достижимых полях частота
, тем выше частота прецессии. При реально достижимых полях частота 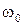 расположена в диапазоне сверхвысоких частот. Из выражения для
расположена в диапазоне сверхвысоких частот. Из выражения для 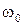 можно сделать неправильный вывод о том, что резонансная частота может быть сделана сколь угодно малой при уменьшении статического поля
можно сделать неправильный вывод о том, что резонансная частота может быть сделана сколь угодно малой при уменьшении статического поля 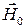 . На самом деле это не так, поскольку при малых полях
. На самом деле это не так, поскольку при малых полях 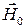 в ферромагнетике наблюдаются другие явления, определяющиеся внутренними полями ферромагнетика, рассмотрение которых выходит за рамки настоящей работы.
в ферромагнетике наблюдаются другие явления, определяющиеся внутренними полями ферромагнетика, рассмотрение которых выходит за рамки настоящей работы.
Электромагнитные волны в феррите.
Тензор магнитной проницаемости
Предположим, что в намагниченном феррите распространяется электромагнитная волна с несовпадающим по направлению с вектором напряженности магнитного поля 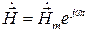 . Тогда уравнение движения намагниченности (5.12) примет вид:
. Тогда уравнение движения намагниченности (5.12) примет вид:
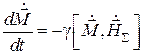 , (5.15)
, (5.15)
где 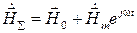 .
.
Поскольку вектор  изменяется по гармоническому закону, то ориентация результирующего вектора
изменяется по гармоническому закону, то ориентация результирующего вектора 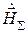 будет меняться с частотой
будет меняться с частотой 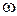 . Это вызовет так называемую вынужденную прецессию вектора намагниченности, которая будет незатухающей, ибо нет определенного направления, параллельно которому могли бы установиться магнитные моменты.
. Это вызовет так называемую вынужденную прецессию вектора намагниченности, которая будет незатухающей, ибо нет определенного направления, параллельно которому могли бы установиться магнитные моменты.
Если частота электромагнитного поля равна частоте ферромагнитного резонанса, то энергия поля будет тратиться на поддержание прецессии.
В этом случае будет наблюдаться резкое увеличение потерь – резонансное поглощение.
Если считать, что феррит намагничен до насыщения, т. е. все элементарные магнитные моменты ориентированы по постоянному полю 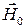 (в отсутствие переменного поля
(в отсутствие переменного поля  ), то намагниченность равна намагниченности насыщения
), то намагниченность равна намагниченности насыщения 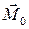 . Суммарная намагниченность равна:
. Суммарная намагниченность равна:
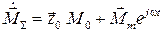 .
.
Рассмотрим случай малого сигнала, т. е. 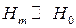 ,
, 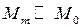 . Подставив в (5.15)
. Подставив в (5.15) 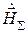 и
и 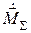 , получим:
, получим:
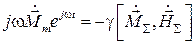 . (5.16)
. (5.16)
Далее, преобразуем векторное произведение в правой части с учетом малости сигнала (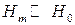 ,
, 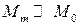 ):
):
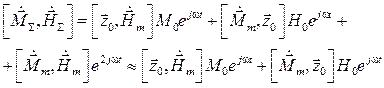 (5.17)
(5.17)
С учетом приближенного равенства (5.17) уравнение (5.16) примет вид:
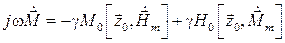 . (5.18)
. (5.18)
Разложим 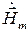 и
и 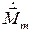 по декартовым осям:
по декартовым осям:
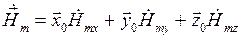 ,
,
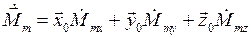 .
.
Тогда уравнение (5.18) можно записать в следующих проекциях:
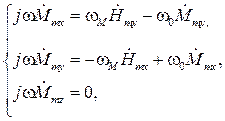 (5.19)
(5.19)
где 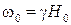 − частота ферромагнитного резонанса;
− частота ферромагнитного резонанса; 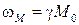 − параметр, имеющий размерность частоты, определяемый свойствами феррита.
− параметр, имеющий размерность частоты, определяемый свойствами феррита.
Решение системы (5.19) для компонент вектора намагниченности дает:
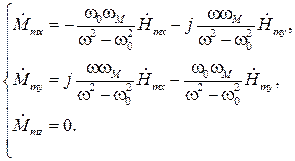 (5.20)
(5.20)
Комплексная амплитуда вектора магнитной индукции определяется известным равенством:
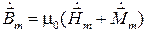 . (5.21)
. (5.21)
Проецируя уравнение (5.21) на декартовы оси и подставляя соответствующие значения 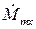 ,
, 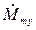 и
и 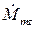 из системы (5.20), получаем:
из системы (5.20), получаем:
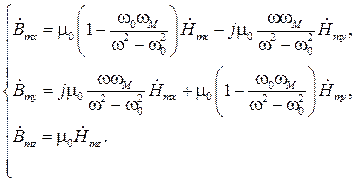 . (5.22)
. (5.22)
Запишем полученную систему (5.22) в матричном виде:
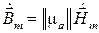 . (5.23)
. (5.23)
Здесь 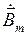 и
и 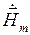 − векторы-столбцы:
− векторы-столбцы:
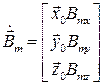 ,
, 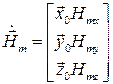 ,
,
а 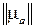 представляет собой матрицу:
представляет собой матрицу:
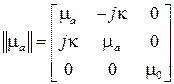 , (5.24)
, (5.24)
где
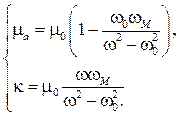 , (5.25)
, (5.25)
Матрица 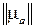 называется тензором абсолютной магнитной проницаемости феррита.
называется тензором абсолютной магнитной проницаемости феррита.
Обратим внимание на то, что в анизотропной гиромагнитной среде векторы 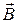 и
и 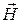 не параллельны в пространстве. Это следует из системы (5.22).
не параллельны в пространстве. Это следует из системы (5.22).
Предположим, что в намагниченном до насыщения феррите распространяется электромагнитная волна, вектор 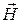 которой поляризован по кругу в плоскости, перпендикулярной вектору
которой поляризован по кругу в плоскости, перпендикулярной вектору 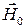 , т. е. в плоскости XОY (рис. 5.7).
, т. е. в плоскости XОY (рис. 5.7).
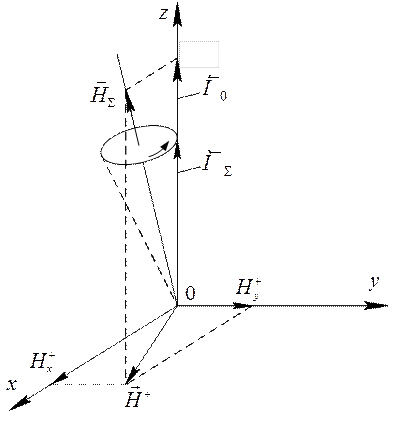
Рис. 5.7. Прецессия вектора намагниченности в присутствии
высокочастотного магнитного поля.
Обозначим через 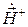 вектор, вращающийся по часовой стрелке, если смотреть вдоль направления вектора
вектор, вращающийся по часовой стрелке, если смотреть вдоль направления вектора 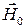 :
:
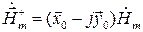 . (5.26)
. (5.26)
Тогда вектор с противоположным направлением вращения будет равен:
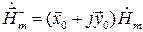 . (5.27)
. (5.27)
Подставим в систему (5.20) вместо 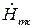 и
и 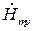 их значения из уравнения (5.26):
их значения из уравнения (5.26):
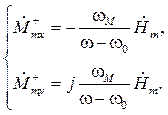 (5.28)
(5.28)
Таким образом, получим:
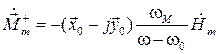 . (5.29)
. (5.29)
Тогда магнитная индукция в соответствии с (5.21) будет равна:
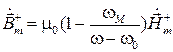 . (5.30)
. (5.30)
Отсюда видно, что вектор 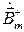 также поляризован по кругу и вращается в ту же сторону, что и вектор
также поляризован по кругу и вращается в ту же сторону, что и вектор 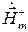 . Естественно считать коэффициентом пропорциональности между
. Естественно считать коэффициентом пропорциональности между 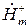 и
и 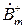 в выражении (5.30) магнитную проницаемость для волны с правым вращением:
в выражении (5.30) магнитную проницаемость для волны с правым вращением:
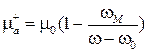 . (5.31)
. (5.31)
Аналогично получим выражения для волны с левым вращением:
|
|