Электродинамика и распространение радиоволн 2 страница

По данным, полученным в ходе измерения КСВН и фазового угла нагрузки, определить нормированное сопротивление нагрузки:

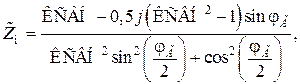(1.11)

где 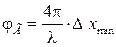, [рад].

Значение нормированного сопротивления нагрузки записать в следующем виде: 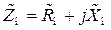, т. е. выделить вещественную и мнимую части нормированного комплексного сопротивления нагрузки и указать характер ее реактивности (индуктивный или емкостной).

Содержание отчета

1. Схема лабораторной установки.

2. Результаты измерений длины волны в волноводе, расчет длины волны в волноводе и частоты, на которую настроен генератор.

3. Градуированная характеристика детектора.

4. Расчет полного сопротивления нагрузки.

5. Краткая сводка результатов всех проведенных измерений и расчетов.

6. Выводы по полученным результатам.

Контрольные вопросы

1. Что такое измерительная линия? Что определяют с помощью измерительной линии? Устройство и принцип действия измерительной линии.

2. Пределы модуля коэффициента отражения, КСВН и КБВ, связь между этими коэффициентами. Каким режимам в измерительной линии соответствуют их предельные значения?

3. В результате чего в измерительной линии устанавливается картина стоячих волн?

4. Чему равен период структуры полей стоячих волн в измерительной линии?

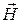5. Волна типа H ₁₀ в прямоугольном волноводе, векторы и , поверхностные токи. Почему щель в измерительной линии располагается посередине широкой стенки?

6. Эпюры токов и напряжений в линии при различных нагрузках.

7. Доказать, что нормированное сопротивление в сечении, в котором расположен минимум стоячей волны, равно КСВН.

8. Какую компоненту стоячих электромагнитных волн мы измеряем с помощью зонда, представленного на рис. 1.1?

9. Каковы источники основных погрешностей измерений в измерительной линии?

10. Как и для чего производится градуировка измерительной линии?

11. Как определяется фазовый угол коэффициента отражения от нагрузки?

Лабораторная работа № 2

ИССЛЕДОВАНИЕ ПРЯМОУГОЛЬНОГО
МЕТАЛЛИЧЕСКОГО ВОЛНОВОДА

Цель работы: экспериментальное исследование электрического и магнитного полей волны H ₁₀ в прямоугольном металлическом волноводе.

Краткие теоретические сведения

В работе проводится исследование поля волны H ₁₀ в прямоугольном волноводе (рис. 2.1), изучается распределение напряженностей электрического и магнитного полей в поперечном сечении волновода, определяются картины поля и токов.

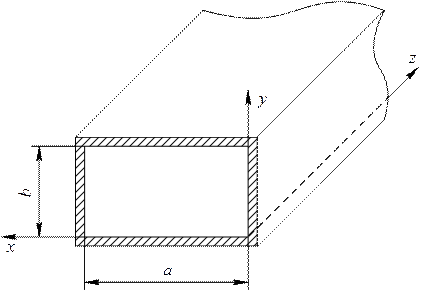
Рис. 2.1. Прямоугольный металлический волновод.

1. Определение рабочего диапазона и длины волны в волноводе
(п. 1 расчетного задания, п. 3 лабораторного задания).

Для оценки диапазона волн, в котором волновод может быть применен при использовании волны типа H ₁₀ в чистом виде, нужно воспользоваться условием единственности существования волны этого типа: 2 а > λ > а;
λ > 2 b. Необходимо уметь выводить данное условие (см. [1], стр. 146− 150), зная, что критическая длина волны H ₁₀ равна 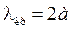и распространение электромагнитной волны в волноводной системе возможно только при 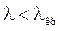. Следует четко себе представлять, что такое фазовая скорость, длина волны в волноводе, критическая частота, простейшие типы волн и соответствующие конфигурации полей. Нужно помнить, что в прямоугольном волноводе длина волны 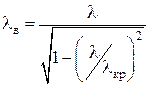больше длины волны λ в свободном пространстве.

2. Исследование распределения поля в волноводе (п. 2 расчетного задания, п. 4, 5 лабораторного задания).

Построение картин поля в прямоугольном волноводе можно провести по методике, предлагаемой в [1], стр. 150− 158.

Для исследования распределения поля в поперечном сечении волновода необходимо определить составляющие поля. Их можно получить из выражений для поля волн магнитного типа 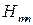, приведенных в [1], стр. 139− 146.

В качестве примера запишем выражения для составляющих электромагнитного поля волны H ₁₀ (m =1, n =0):

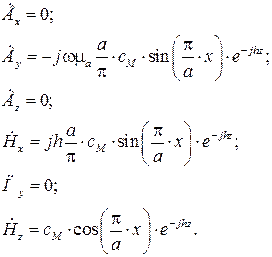(2.1)

Здесь 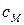− это амплитудный коэффициент;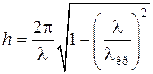
− продольное волновое число.

При построении графиков распределения поля в сечении волновода следует использовать нормированный масштаб по оси ординат. Нормировка проводится по максимальному значению функции.

Рассмотрим пример получения нормированной зависимости составляющей электрического поля волны H ₁₀ от x 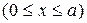. Пользуясь соотношениями (2.1), запишем выражение для модуля комплексной амплитуды электрического поля в виде:

,

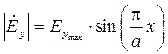где .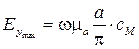

Тогда нормированная зависимость имеет вид:

.

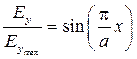Построение полученной зависимости не вызывает трудностей.

3. Построение картин распределения токов в стенках волновода (п. 3 расчетного задания).

Для этого необходимо знать вектор поверхностной плотности тока проводимости 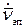. Величина и направление 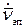определяются из граничных условий для тангенциальных составляющих магнитного поля у идеального металла по формуле:

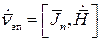(2.2)

Здесь 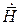− вектор магнитного поля у стенки волновода; 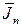− нормаль, направленная к поверхности из металла.

4. Определение типа щели (излучающая или неизлучающая) в волноводе с волной заданного типа (п. 3 задания, выполняемого при подготовке).

Здесь необходимо провести исследование распределения поверхностных токов на стенках волновода согласно (2.2). В волноводной технике щелью называют прямоугольное отверстие, длина которого значительно превосходит ширину. Если щель пересекает линии поверхностного тока, то она – излучающая. Если щель прорезана параллельно линиям тока, то она является неизлучающей. В качестве примера на рис. 2.2. на стенках прямоугольного волновода с волной H ₁₀ изображены излучающие (1, 3) и неизлучающая (2) щели.

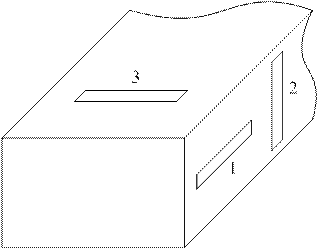
Рис. 2.2. Излучающие и неизлучающие щели.

При выполнении задания в лаборатории необходимо помнить, что волну в волноводе можно возбудить:

а) проводником (штырем) с током, расположив его вдоль направления вектора напряженности электрического поля в тех местах, где это поле должно иметь максимальное значение;

б) рамкой (петлей) с током, поместив ее в волноводе там, где напряженность магнитного поля должна быть максимальной. Плоскость рамки необходимо ориентировать перпендикулярно магнитным силовым линиям;

в) щелью, которую необходимо прорезать перпендикулярно силовым линиям тока, протекающего по стенкам волновода. На щели с помощью внешнего источника должно быть создано электрическое поле, силовые линии которого продолжали бы линию тока.

Обычно волновод на одном конце линии закрывается проводящей стенкой (подвижным поршнем), вследствие чего передача энергии происходит только в одну сторону. Величина мощности, отдаваемой источником в волновод (интенсивность возбуждения), зависит от расстояния z ₀ между возбуждающим элементом и поршнем (п. 2 задания, выполняемого в лаборатории).

Наибольшая интенсивность возбуждения получается, если расстояние 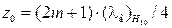, где m − любое целое число, в том числе и ноль. Согласно теореме взаимности, конструкции устройств, используемых для извлечения энергии из волновода и для возбуждения поля в этом же волноводе, должны быть одинаковыми. В связи с этим извлечь энергию из волновода можно так же с помощью штыря, рамки или щели.

При подготовке к выполнению лабораторной работы необходимо иметь в виду, что при анализе поля в реальных волноводах выражения для составляющих поля определяют, считая материалы стенок идеальными. В действительности конечная проводимость стенок приводит к тому, что структура поля в реальном волноводе отлична от случая идеального волновода.

Так как проводимость реальных материалов, используемых для волноводов, весьма высока (σ ~ 10⁷ См/м), то можно считать, что структура электромагнитного поля волны в реальном волноводе мало отличается от структуры поля в волноводе со стенками из идеального металла.

Затухание волн, вызываемых омическими потерями в стенках волновода, невелико. Однако при достаточно большой длине волноводной линии передачи полное затухание может быть весьма ощутимым, поэтому важно знать величину коэффициента затухания (см. [1], с. 208− 213).

Для волны H ₁₀ в прямоугольном волноводе затухание поля на единицу длины можно найти по формуле:

.

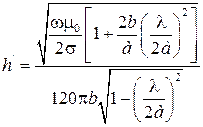где σ – удельная проводимость металла, которым покрыты внутренние стенки волновода.

Описание экспериментальной установки

На рис. 2.3 изображена схема установки для исследования поля волны H ₁₀ в волноводе прямоугольного сечения размером 23× 10 мм, которая состоит из измерительной волноводной линии 1 и секций, соединенных фланцами.

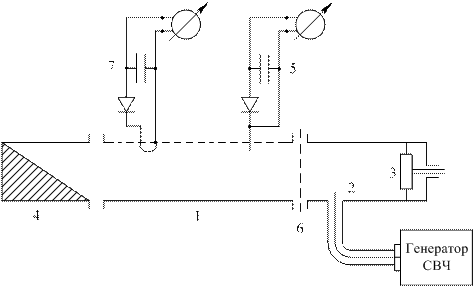
Рис. 2.3. Схема установки для исследования электромагнитного поля в волноводе.

Источником колебаний в данной работе служит генератор, работающий в сантиметровом диапазоне волн. СВЧ-колебания по коаксиальному кабелю поступают к штырю 2, являющемуся возбудителем поля в волноводе. Подвижной поршень 3 используется для согласования выходного сопротивления возбуждающего устройства (штыря) с волноводом. При согласовании получаем наиболее интенсивное возбуждение волновода. На конец волновода может подключаться закорачивающая пластина или поглощающая нагрузка 4, представляющая собой отрезок волновода, куда вставлено несколько поглощающих пластинок, расположенных параллельно электрическим силовым линиям поля волны типа H ₁₀. Отрезок волновода с продольной щелью
в широкой стенке, вдоль которой перемещается измерительная каретка с зондом-штырем 5, проходящим внутрь волновода, является волноводной измерительной линией. Зонд линии через детектор соединен с микроамперметром, благодаря чему оказывается возможным измерять относительные значения напряженности электрического поля в волноводе. В одном из фланцевых соединений сделан специальный зазор 6 для введения в волновод фильтров − металлических решеток, щели в которых прорезаны параллельно широкой (рис. 2.4 а) или узкой (рис. 2.4 б) стенке волновода.

Для изучения распределения напряженности магнитного поля в поперечном сечении волновода служит измерительная каретка с зондом-петлей 7. Так как в широкой стенке прямоугольного волновода с волной типа H ₁₀ нельзя прорезать поперечную щель, не нарушив распределения поля в волноводе, зонд этой измерительной линии движется вместе с притертой крышкой в верхней стенке.

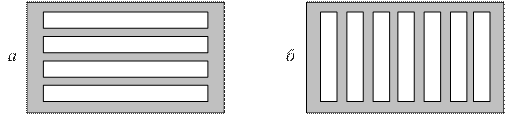
Рис. 2.4. Решетчатые фильтры.

Таким образом, для измерения напряженности электрического поля в качестве зонда используется небольшой штырь, вводимый в волновод, а для измерения напряженности магнитного поля – небольшая петля. Конструктивно электрический и магнитный зонды выполнены в виде отдельных детекторных блоков, вставляемых в отверстие в притертой крышке по мере необходимости. К лабораторной установке прилагается несколько отрезков прямоугольных волноводов с прорезанными узкими щелями.

Домашнее задание

1. Рассчитать длину волны H ₁₀ в волноводе, если генератор СВЧ работает на частоте 10 ГГц.

Оценить диапазоны длин волн и частот, в которых волновод может быть применен при использовании волны типа H ₁₀. Проверить, выполняется ли условие невозможности существования волны типа H ₁₀.

2. Изобразить картину поля волны типа H ₁₀ в прямоугольном волноводе.

Построить следующие графики составляющих поля волны типа в поперечном сечении волновода:

; ; .

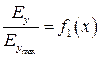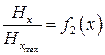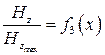3. Построить картину распределения токов в стенках волновода в слу-чае волны типа H ₁₀. Изобразить на рисунке щели, являющиеся излучающими и неизлучающими, в волноводах с волнами заданного типа.

Порядок выполнения работы

1. Включить генератор СВЧ. Добиться максимальной интенсивности возбуждения поля в волноводе. Интенсивность возбуждения оценивать по показаниям индикатора измерительной линии.

2. Снять зависимость интенсивности возбуждения волновода от положения поршня. Изучение влияния положения поршня на интенсивность возбуждения произвести с помощью индикатора волноводной измерительной линии. Для этого вставить в измерительную линию электрический зонд-штырь и, перемещая каретку, установить его в середине линии. Интенсивность возбуждения измерительной линии можно отслеживать по показаниям индикатора зонда. При этом к концу волноводной линии необходимо присоединить поглощающую нагрузку.

Расстояние между вибратором и поршнем изменять плавно от 0, 5 до
2, 5 см. Следует особо отметить расстояния, при которых получается минимальная и максимальная интенсивность возбуждения.

По данным опыта построить график зависимости интенсивности возбуждения от положения поршня.

При выполнении остальных пунктов лабораторного задания расстояние между возбуждающим штырем и поршнем следует сделать таким, при котором получается наиболее интенсивное возбуждение волновода.

3. Измерить длину волны в волноводе с помощью измерительной линии и сравнить ее с расчетной. Измерение длины волны производится по расстоянию между двумя последовательными минимумами напряженности электрического поля. Это расстояние будет равняться половине длины волны в волноводе. Длину волны измерять при таких условиях, когда в волноводе имеет место стоячая волна. Для этого в волноводе следует поместить отражающую стенку. В качестве отражающей стенки можно использовать электрический фильтр с щелями, прорезанными параллельно боковым стенкам волновода, или закорачивающую пластину.

4. Изучить картину электрического поля волны типа H ₁₀ в прямоугольном волноводе. Для этого в волновод последовательно ввести оба фильтра и с помощью зонда-штыря в поперечной измерительной линии определить, изменилась ли интенсивность поля в волноводе за фильтром. Если, например, решетчатый фильтр, показанный на рис. 2.4 а, после введения в волновод не оказывает влияния на распространение волны, то это значит, что в волноводе распространяется такая электромагнитная волна, электрическое поле которой параллельно боковым стенкам волновода. Если вставить в волновод второй фильтр, то в волноводе должна установиться стоячая волна. Таким образом, вводя в волновод фильтры, можно сделать заключение об ориентации вектора напряженности электрического, а, следовательно, и магнитного полей.

5. Исследовать поле в поперечном сечении волновода. В поперечном сечении волновода поле изучить при таких условиях, когда в волноводе имеет место стоячая волна. Для этого на конец волновода подключить подвижный закорачивающий поршень.

Исследование электрического поля в поперечном сечении осуществляется с помощью зонда-штыря в измерительной линии, а магнитного поля – зонда в виде петли. ЭДС, наведенная в петле, пропорциональная напряженности магнитного поля в волноводе вблизи широкой стенки.

Установить в поперечной измерительной линии зонд-штырь. Микроамперметр подключить к клеммам 1− 2 детекторного блока измерительной каретки (рис. 2.5 а). Установить зонд-штырь в середине широкой стенки волновода и, изменяя положение подвижного поршня, добиться максимального показания прибора. Не изменяя положения поршня, снять зависимость:

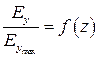при y = const. (2.3)

Измерения производить через каждые 0, 2 см перемещения зонда от одного края измерительной линии до другого.

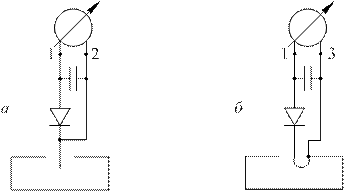
Рис. 2.5. Продольный (а) и поперечный (б) зонды.

Аналогичным образом для исследования магнитного поля установить в поперечной измерительной линии зонд-петлю. Микроамперметр подключить к клеммам 1− 3 детекторного блока измерительной каретки (рис. 2.5 б). При исследовании магнитного поля необходимо правильно установить плоскость петли для измерения 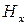. После установки зонда-петли в середине широкой стенки волновода, изменяя положение подвижного поршня, добиться максимального показания прибора. Закрепить поршень в этом положении контргайкой.

Далее, не изменяя положения подвижного поршня, снять зависимость:

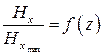при y = const. (2.4)

Убедиться, что при определенных положениях зонда-петли .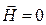

После измерений построить графики указанных выше зависимостей (2.3), (2.4). При построении графиков учесть тот факт, что зонд не может быть установлен вплотную к краям измерительной линии.

6. Исследовать, какие щели в волноводе являются излучающими, а какие неизлучающими при волне H ₁₀. Для этого провести поочередно измерение коэффициента бегущей волны в прямоугольном волноводе, на выходе которого поочередно подключаются четыре отрезка волновода с различными прорезанными щелями. Волноводные отрезки следует подключать на выходе измерительной линии 1 вместо поглощающей нагрузки 4 или короткозамыкающей пластины (см. рис. 2.3). Исследуемый отрезок волновода на выходе замкнуть короткозамыкающей пластиной. Измерение коэффициента бегущей волны проводить с помощью измерительной линии. Измерить напряженность поля в минимуме и максимуме волны. Коэффициент бегущей волны рассчитать по формуле:

.

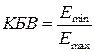Зная коэффициент бегущей волны, определить коэффициент отражения:

,

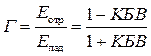по которому оценить, какая щель в волноводе излучает энергию электромагнитного поля, а какая не излучает.

Предварительно убедиться, что коэффициент отражения волны от закороченного на конце волновода без щели равняется единице вследствие малости затухания поля за счет потерь в стенках волновода. Излучение энергии электромагнитного поля щелью, прорезанной в волноводе, приводит к уменьшению коэффициента отражения волны.

7. Выключить блок питания генератора.

Содержание отчета

1. Расчеты и рисунки, выполненные по разделу «Домашнее задание».

2. Расчеты и рисунки, полученные при выполнении раздела «Порядок выполнения лабораторной работы».

3. Краткая сводка результатов всех проведенных измерений и расчетов.

4. Выводы по полученным результатам (краткое сравнение теоретических и экспериментальных данных с необходимыми пояснениями).

Контрольные вопросы

1. Как показать, что электромагнитное поле волны H ₁₀ не может иметь компоненты электрического поля E_x?

2. Почему фильтр с щелями, параллельными узкой стенке волновода, препятствует распространению волны типа H ₁₀ в прямоугольном волноводе?

3. Почему наиболее интенсивное возбуждение волновода получается при расстоянии между поршнем и штырем примерно кратным нечетному числу четвертой длины волны в волноводе?

4. Как влияют размеры волновода на длину волны в волноводе при неизменной частоте электромагнитных колебаний?

5. Как изменится затухание волновода в случае волны H ₁₀, если увеличить размер а волновода, размер b волновода?

6. Какая волна в прямоугольном волноводе является основной для волн электрического поля и почему?

Лабораторная работа № 3

ОБЪЕМНЫЙ РЕЗОНАТОР

Цель работы: изучить резонансные свойства объемного резонатора, определить ширину его полосы пропускания и добротность.

Краткие теоретические сведения

В диапазоне СВЧ трудно (а то и просто невозможно) создать колебательные контуры из сосредоточенных элементов с высокой добротностью. Поэтому в этом диапазоне колебательные системы строят из элементов с распределенными параметрами (отрезки двухпроводной, коаксиальной, полосковой линии, волноводов и др.). Из уравнения Максвелла следует, что в изолированном от внешнего пространства объеме, заполненном средой без потерь (как и в объемном контуре без потерь), может существовать, незатухающий колебательный процесс. Такие системы получили название
объемных резонаторов. Например, резонатором будет объем, ограниченный со всех сторон металлической поверхностью (короткозамкнутый отрезок коаксиальной линии или металлического волновода).

Основным преимуществом объемных резонаторов по сравнению с контурами из сосредоточенных элементов является отсутствие потерь на излучение вследствие полной экранировки поля стенками резонатора и отсутствия потерь в диэлектрике, так как принципиально введение диэлектриков внутрь резонатора не является необходимым.

Тепловые потери в металлической оболочке резонатора также значительно меньше, чем в проводниках обычных контуров из сосредоточенных элементов, благодаря большой внутренней поверхности, по которой протекают высокочастотные токи.

Следует отметить, что в отличие от обычных контуров объемные резонаторы резонируют не на одной частоте, а на бесконечном множестве дискретных частот. Причем каждой резонансной частоте соответствует определенная структура поля в резонаторе. Низшим колебанием называют такое, которому при заданных размерах резонатора соответствует минимальная резонансная частота. Если резонансные частоты двух или нескольких видов колебаний равны между собой, то такие виды колебаний называются
вырожденными.

Устройство и принцип действия объемного резонатора

Основными параметрами, характеризующими объемные резонаторы, являются следующие:

1) резонансная длина волны λ _рез (или резонансная частота );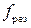

2) добротность Q;

3) активная проводимость σ.

В общем случае резонансную длину волны и структуру поля в объемном резонаторе находят из решения волнового уравнения при граничных условиях, определяемых формой и геометрическими размерами резонатора. Решение подобной задачи существенно упрощается, если резонатор образован из отрезка линии передачи с известной структурой электромагнитного поля.

Добротность объемного резонатора определяется по формуле:

, (3.1)

где 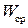− среднее за период значение запасенной в резонаторе энергии;
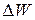− изменение энергии в резонаторе за период.

В общем случае потери в резонаторе можно определить следующим образом:

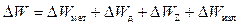. (3.2)

Здесь 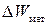− энергия потерь за период колебаний в оболочке резонатора; − энергия потерь за период колебаний в среде, заполняющей резонатор; 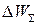− энергия, отдаваемая резонатором во внешние устройства; 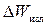− энергия, теряемая на излучение.

Полную добротность можно представить в виде:

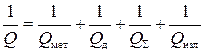, (3.3)

где

.

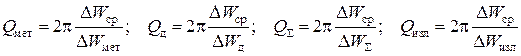Полную добротность Q называют нагруженной добротностью резонатора; и 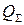– соответственно радиационной и внешней добротностью. Внешнюю добротность 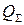еще называют добротностью связи.

В технике СВЧ широкое распространение получили объемные резонаторы в виде короткозамкнутых отрезков регулярных линий передачи. Такие резонаторы обычно создают из отрезков линий передачи длиной l, замкнутых накоротко с обеих сторон с помощью металлических пластин.

При возбуждении колебаний в резонаторах такого типа вдоль их продольной оси устанавливается стоячая волна, у которой в соответствии с граничными условиями на торцевых закорачивающих пластинах находятся узлы поперечной составляющей напряженности электрического поля и пучности поперечной составляющей магнитного поля.

Поэтому длина объемного резонатора равна целому числу полуволн электромагнитной волны, распространяющейся по регулярной линии передачи:

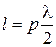, (3.4)

где р − количество полуволн стоячей волны λ, устанавливающейся вдоль продольной оси резонатора (p = 1, 2, 3...). Подставив сюда выражение 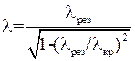, определим резонансную длину волны λ _рез рассматриваемого резонатора:

, (3.5)

где λ _кр − критическая длина волны определенного типа, распространяющейся в линии передачи.

Классификация колебаний в таких объемных резонаторах производится в соответствии с типом волны (T, E_mn или 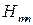), стоячая волна которой образуется в резонаторе. Чтобы различать колебания с различным числом полуволн, укладывающихся вдоль продольной оси резонатора, вводят дополнительный индекс p, смысл которого остается тем же, что и для формул (3.4) и (3.5).