Электродинамика и распространение радиоволн 5 страница

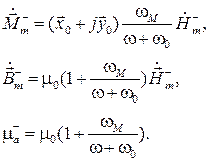(5.32)

Видно, что в намагниченном феррите 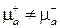. Проницаемост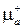и и 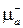можно выразить через элементы тензора магнитной проницаемости (5.24):

(5.33)

Как было показано, направление свободной прецессии совпадает с направлением вращения волны 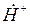. Следовательно, для поддержания свободной прецессии в феррите должна распространяться электромагнитная волна с частотой 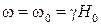и правым направлением вращения плоскости поляризации. При этом волна 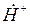испытывает наибольшее поглощение.

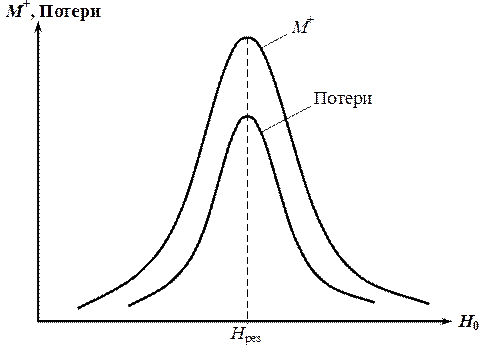
Рис. 5.8. Зависимости намагниченности для правого вращения и потерь в феррите от величины поля подмагничивания вблизи его резонансного значения.

Поскольку частота ферромагнитного резонанса 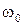пропорциональна величине подмагничивающего поля 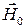, то поведение параметров феррита можно выразить через эту величину (рис. 5.8). Напротив, волна 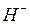проходит через феррит с малыми потерями.

Рис. 5.9. Зависимость относительных магнитных проницаемостей для электромагнитных волн с правым и левым вращением от поля подмагничивания.

На рис. 5.9 показана зависимость проницаемосте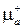й и 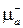от величины постоянного поля 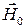. Значение поля 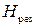соответствует гиромагнитному резонансу, т. е. случаю, когда .

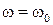Рассмотрим, как будут записываться уравнения Максвелла в намагниченном феррите. Исходим из обычной записи для монохроматического поля в среде без потерь:

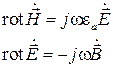(5.34)

Координатные значения компонент вектора 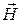следует выбирать из системы (5.22). В этом случае получим:

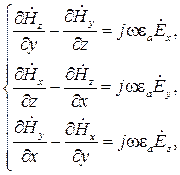(5.35)

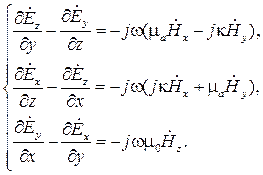(5.36)

Невзаимные явления в поперечно-намагниченном феррите

Подавляющее большинство вентилей СВЧ строятся на поперечно-намагниченных ферритах, поэтому их и будем рассматривать.

Гиромагнитный резонанс. Как следует из рис. 5.8, волна 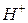с положительным относительно 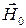вращением плоскости поляризации вектора 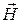на частоте 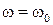интенсивно поглощается. Волна с противоположным вращением проходит через феррит почти без затухания. Это свойство ферритов может быть использовано в невзаимных устройствах – вентилях.

Рис. 5.10. Магнитное поле волны H ₁₀ в прямоугольном волноводе.

На рис. 5.10 показано магнитное поле волны H ₁₀ в прямоугольном волноводе. На расстоянии от боковых стенок, равном примерно 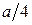, вектор 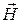поляризован по кругу, причем направления вращения слева и справа от продольной плоскости симметрии волновода будут противоположными. Если поместить на этом расстоянии, т.е. в область круговой поляризации магнитного поля, ферритовую пластину, подмагниченную полем 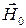(рис. 5.11), то коэффициенты затухания для волн, распространяющихся в разных направлениях, на резонансной частоте 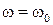будут различными.

При отстройке от гиромагнитной частоты 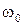затухание волны 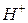уменьшается в соответствии с ходом резонансной кривой, который определяется добротностью феррита.

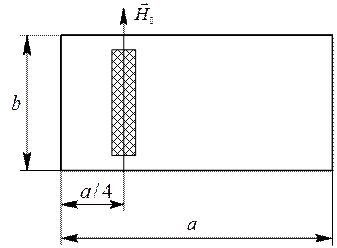
Рис. 5.11. Намагниченная ферритовая пластина в прямоугольном волноводе.

Вентили, построенные на использовании явления гиромагнитного резонанса, из-за узкополосности рабочей полосы частот и большой величины подмагничивающего поля применяются в технике СВЧ редко.

Поперечный ферромагнитный резонанс. Предположим, что плоская электромагнитная волна распространяется вдоль оси х с коэффициентом распространения β _х (рис. 5.7). Положим в (5.35) и (5.36), 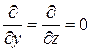. Тогда системы уравнений (5.36) и (5.35) преобразуются к виду:

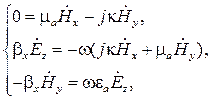(5.37)

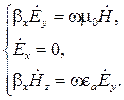(5.38)

Исключим 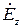из (5.37):

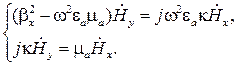(5.39)

Отсюда находим значение коэффициента распространения:

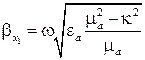(5.40)

В соответствии с (5.37) у волны с коэффициентом распространения 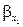вектор магнитного поля лежит в плоскости 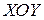, перпендикулярной вектору подмагничивающего поля 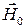, и при 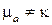имеет эллиптическую поляризацию. Вектор электрического поля волны параллелен постоянному магнитному полю. Наличие составляющей 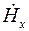, параллельной направлению распространения (ось ОX), означает, что система (5.37) описывает волну Н -типа.

Аналогично, исключая 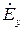из системы (5.38), получаем:

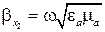(5.41)

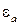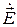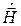У этой волны, согласно (5.38), вектор магнитного поля ориентирован параллельно направлению постоянного магнитного поля. В этом случае магнитное поле волны не возбуждает прецессии магнитного момента и коэффициент распространения такой же, как в немагнитной среде с той же диэлектрической проницаемостью , что и у феррита. Составляющие векторов и перпендикулярны направлению распространения, т. е. эта волна является волной Т -типа (поперечной волной).

Подставив в (5.40) значения 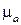и 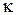из (5.33), получим:

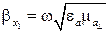, (5.42)

где

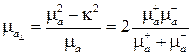, (5.43)

Из графика, приведенного на рис. 5.9, видим, что 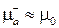. Потому величину 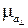можно записать в виде:

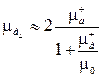. (5.44)

В реальных ферритах диэлектрическая проницаемость является комплексной величиной:

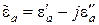. (5.45)

Рассмотрим случай малых диэлектрических потерь в феррите, т. е. 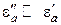. Если пренебречь магнитными потерями, то можно записать следующее:

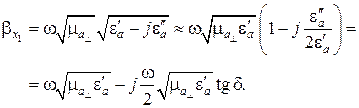(5.46)

Из равенства (5.44) вытекает, что если 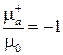, то 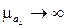. При этом, как следует из выражения (5.46), бесконечно возрастает мнимая часть коэффициента распространения, и распространяющаяся в феррите волна интенсивно затухает. Это соответствует случаю так называемого поперечного ферромагнитного резонанса, который наступает при подмагничивающем поле 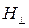(рис. 5.12). Еще раз отметим, что рассмотренное явление не связано с ферромагнитным резонансом, а объясняется наличием диэлектрических потерь в феррите.

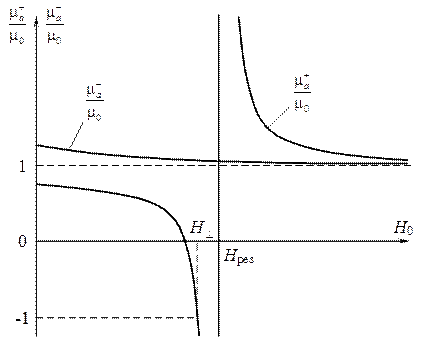
Рис. 5.12. Поперечный ферромагнитный резонанс.

Из рис. 5.12 видим, что поперечный ферромагнитный резонанс наступает при напряженностях поля 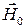, которые меньше, чем поле гиромагнитного резонанса 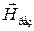. Это облегчает реализацию вентилей.

Как уже было отмечено, в прямоугольном волноводе область круговой поляризации магнитного поля существует на расстоянии 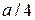от боковых стенок (рис. 5.11). При повышении частоты эта область смещается к узкой стенке, при понижении частоты – к середине волновода. Для ослабления влияния частоты на структуру поля рядом с ферритовой пластиной помещают диэлектрик с высокой диэлектрической проницаемостью (рис. 5.13). Диэлектрик концентрирует в себе (втягивает) электромагнитное поле, тем самым ослабляя зависимость структуры поля от частоты.

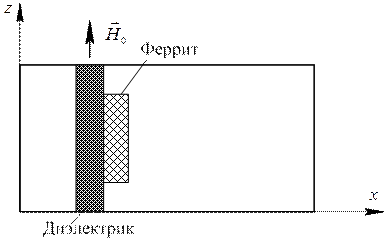
Рис. 5.13. Поперечное сечение вентиля, в котором используется
явление поперечного ферромагнитного резонанса.

Явление смещения поля. Как следует из формулы (5.33), при 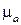< 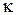магнитная проницаемость 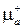становится отрицательной. При этом коэффициент распространения 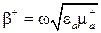становится мнимой величиной, что соответствует волне с амплитудой, убывающей вдоль направления распространения. Если ферритовая пластина безгранична, то электромагнитная волна отражается. Если ферритовый образец имеет ограниченные размеры, то волна вытесняется из феррита и огибает его при распространении.

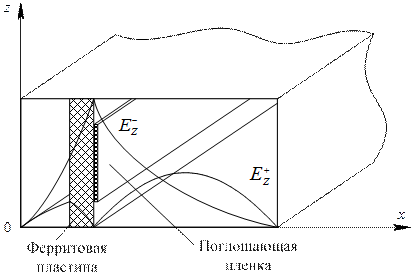
Рис. 5.14. Вентиль на смещении поля.

Конструктивно вентиль на смещении поля подобен резонансному
(рис. 5.14), но в данном случае на феррит нанесена поглощающая пленка, например, из графита. Волна с магнитной проницаемостью 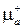вытесняется из феррита и распространяется вне его, поэтому напряженность поля 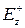в поглощающем слое мала и затухание незначительно. Волна с поляризацией концентрируется в феррите, напряженность поля 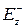у поверхности феррита велика, в поглощающем слое наводится значительный ток проводимости, и волна интенсивно затухает.

Описание лабораторной установки

В настоящей работе для измерения амплитудно-частотных характеристик (АЧХ) вентилей в прямом и обратном направлениях применяется измеритель модуля коэффициента передачи и отражения «Р2М-04» российской фирмы «Микран» (г. Томск). Схема измерения АЧХ исследуемых вентилей с помощью этого измерителя представлена на рис. 5.15.

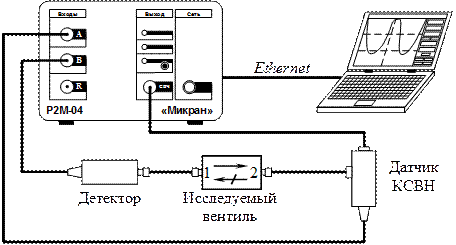
Рис. 5.15. Схема измерения амплитудно-частотных характеристик исследуемых вентилей
с помощью прибора «Р2М-04».

Входной сигнал, пропорциональный уровню мощности (отраженной – при измерении модуля коэффициента отражения; падающей – при измерении модуля коэффициента передачи) СВЧ-колебаний, оцифровывается и считывается процессором цифровой обработки сигналов измерителя, который, выполнив необходимые вычисления, передаёт результаты в ЭВМ. Контроль и измерение амплитудно-частотных характеристик резонатора осуществляется на мониторе компьютера с помощью частотных меток.

Для устранения потерь, вносимых трактом, непосредственно перед измерением необходимо провести калибровку СВЧ-тракта.

По усмотрению преподавателя для проведения измерений и исследований может быть использован более высокочастотный вентиль. В этом случае вместо измерителя «Р2М-04» следует использовать измеритель «Р2М-18» той же фирмы, который работает в диапазоне до 18 ГГц. Схема измерений АЧХ с помощью измерителя «Р2М-18» аналогична представленной на рис. 5.15.

В настоящей лабораторной работе исследуются вентили, в которых используется эффект поперечного ферромагнитного резонанса.

Порядок выполнения лабораторной работы

Получив у преподавателя допуск и вентиль для исследования, приступить к выполнению лабораторной работы в следующем порядке:

1. Ознакомиться с устройством и назначением измерительной аппаратуры. Проверить правильность соединений приборов по схеме.

2. Включить аппаратуру в сеть согласно инструкции. Прогреть не менее 15 минут.

3. Произвести калибровку СВЧ-тракта, после чего включить исследуемый вентиль в схему измерений АЧХ согласно рис. 5.15.

4. Снять амплитудно-частотные характеристики вентиля (прямые и обратные потери) во всем рабочем диапазоне прибора «Р2М-04» в прямом
(вход 1 → вход 2) и обратном (вход 2 → вход 1) направлениях.

5. По измеренным кривым прямых и обратных потерь для каждого из направлений включения вентиля в СВЧ-тракт построить частотные зависимости его потерь на поглощение (А, дБ).

6. По измеренным кривым прямых потерь для обоих направлений определить, какому включению вентиля в СВЧ-тракт соответствует прямая и обратная волны в вентиле, и определить вентильное отношение вентиля во всем исследованном частотном диапазоне. Результат отобразить на графике.

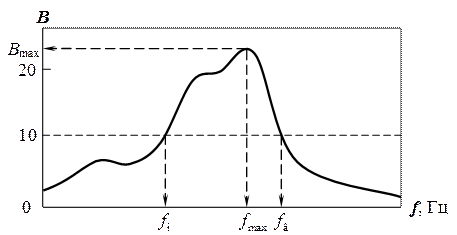
Рис. 5.16. График вентильного отношения исследуемого вентиля
с указанием всех характерных частот и значений.

7. По построенной частотной зависимости вентильного отношения определить ширину рабочей полосы исследуемого вентиля по уровню 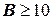относительно центральной частоты этой полосы (∆ f / f ₀, %) по формуле:

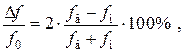. (5.45)

где 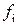и 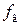– нижняя и верхняя граничные частоты рабочей полосы вентиля (см. рис. 5.16). Также определить значения (частоту, на которой вентильной отношение максимально) и 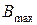(максимальное значение вентильного отношения) согласно рис. 5.16.

Содержание отчета

1. Схема лабораторной установки.

2. Графики частотных зависимостей прямых (L, дБ) и обратных (R, дБ) потерь вентиля для прямого и обратного направлений.

3. Графики частотных зависимостей потерь на поглощение в исследуемом вентиле для обоих направлений его включения в СВЧ-тракт.

4. График частотной зависимости вентильного отношения исследуемого вентиля с указанием его рабочей полосы.

4. Краткая сводка результатов всех проведенных измерений и расчетов.

5. Выводы по полученным результатам.

Контрольные вопросы

1. Что такое ферритовый вентиль, где он применяется?

2. Какими параметрами характеризуется качество ферритов вентиля?

3. Природа магнитных свойств вещества.

4. Что такое прецессия магнитного момента и вектора намагниченности?

5. От чего зависит частота и направление свободной прецессии?

6. Что такое круговая поляризация?

7. Что такое тензор магнитной проницаемости?

8. Физический смысл электродинамических параметров 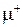и 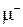, их связь с элементами тензора магнитной проницаемости.

9. Пояснить график зависимости параметров 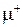и 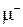от величины подмагничивающего поля .

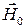10. В чем заключается явление поперечного ферромагнитного резонанса, его отличие от гиромагнитного резонанса?

11. В чем суть явления смещения поля в намагниченном феррите?

12. Как зависит направление круговой поляризации вектора магнитного поля в прямоугольном волноводе на волне Н ₁₀ от направления распространения энергии?

13. В какую область помещается феррит в вентиле на прямоугольном волноводе?

14. Почему при повышении частоты область с круговой поляризацией вектора 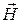смещается к узкой стенке волновода?

15. Назначение диэлектрической пластины в вентиле.

16. Принцип действия и устройство резонансного вентиля.

17. Принцип действия и устройство вентиля на смещении поля.

18. Показать на рисунках с вентилями на гиромагнитном резонансе, на поперечном ферромагнитном резонансе и на смещении поля прямую и обратные волны.

Библиографический список

1. Федоров, Н. Н. Основы электродинамики / Н. Н. Федоров. –
М.: Высш. шк., 1980.

2. Асеев, Б.П. Основы радиотехники / Б.П. Асеев. – М.: Связьиздат, 1947.

3. Вольман В.И., Пименов Ю.В. Техническая электродинамика /
В.И. Вольман. – М.: Изд. «Связь», 1971.

4. Баскаков, С. И. Основы электродинамики / С. И. Баскаков. –
М.: Высш. шк., 1973.

5. Никольский, В.В. Электродинамика и распространение радиоволн /
В.В. Никольский. – М., 1979.

6. Кураев, А.А. Электродинамика и распространение радиоволн / А.А. Кураев, Т.Л. Попкова, А.К. Синицын. – Минск.: Изд. «Бестпринт», 2004.

7. Марков, Г.Т. Электродинамика и распространение радиоволн / Г.Т. Марков, В. М. Петров и др. – М., 1979.

8. Гольдштейн, М.Д. Электромагнитные поля и волны / М.Д. Гольдштейн, Н.В. Зернов. – М., 1971.

9. Лебедев, И. В. Техника и приборы СВЧ: в 2-х ч. Ч. 1 / И. В. Лебедев. –
М.: Высш. шк., 1970.

10. Фрадин, А. З. Измерение параметров антенно-фидерных устройств /
А. З. Фрадин. – М.: Связь, 1972.

11. Стариков, В. Д. Методы измерения на СВЧ с применением измерительных линий / В. Д. Стариков. – М.: Сов. радио, 1972.

12. Баскаков, С. И. Радиотехнические цепи с распределенными параметрами / С. И. Баскаков. – М.: Высш. шк., 1980.

13. Ефимов, И. Е. Радиочастотные линии передачи /И. Е. Ефимов. – М.: Сов. радио, 1964.

14. Зернов, Н. В. Теория радиотехнических цепей / Н. В. Зернов,
В. Г. Карпов – Л.: Энергия, 1973.

15. Фальковский, О.И. Техническая электродинамика / О.И. Фальковский. – М.: Изд. «Лань», 2009.

16. Фиалковский, О.И. Техническая электродинамика / О.И. Фиалковский. – М., 1978.

17. Никольский, В.В. Антенны / В.В. Никольский. – М., 1966.

18. Семенов, Н. А. Техническая электродинамика / Н. А. Семенов. –
М., 1973.

19.Сазонов, Г. М. Устройства СВЧ / Г. М. Сазонов, А. Н. Гридин,
Б. А. Мишустин. – М., 1981.

Оглавление

ВВЕДЕНИЕ.. 3

Лабораторная работа № 1
ИЗМЕРИТЕЛЬНАЯ ЛИНИЯ.. 4

Конструкция и принцип действия измерительных линий. 4

Методика измерения полных сопротивлений. 12

Порядок выполнения работы.. 13

Содержание отчета. 15

Контрольные вопросы.. 16