
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретические сведения. Градиентом функции , который обозначается grad , называется вектор, величина которого (модуль) определяет скорость изменения функции
|
|
Градиентом функции 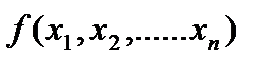 , который обозначается grad
, который обозначается grad 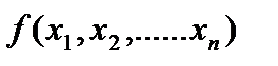 , называется вектор, величина которого (модуль) определяет скорость изменения функции, а направление совпадает с направлением наибольшего возрастания этой функции. Отрицательный вектор градиента - grad
, называется вектор, величина которого (модуль) определяет скорость изменения функции, а направление совпадает с направлением наибольшего возрастания этой функции. Отрицательный вектор градиента - grad 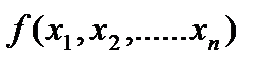 называется антиградиентом и показывает направление наибольшего убывания целевой функции.
называется антиградиентом и показывает направление наибольшего убывания целевой функции.
Если необходимо найти минимальное значение целевой функции, то для каждой точки поиска N надо определить градиент и сделать шаг по направлению антиградиента. Новые значения параметров оптимизации будут определяться из соотношения
 ,
,
где h- длина шага движения (h> 0).
Выбор величины шага зависит от целевой функции, а значит формы многомерного пространства. Если шаг взять большой, то можно проскочить искомый оптимум. При малом шаге уменьшится скорость поиска, что в свою очередь приведет к увеличению объема вычислений, а значит и к погрешности округления.
На практике для ускорения процесса поиска поступают следующим образом. При движении вдали от оптимума шаг имеет постоянную, достаточно большую величину. При входе в зону оптимума происходит уменьшение шага.
Основным преимуществом градиентных методов является высокая точность, так как на каждом шаге производится попытка двигаться в наилучшем направлении.
Для оценки точности поиска оптимума можно использовать два варианта.
1. По модулю градиента функции. При подходе к оптимуму скорость изменения значения функции уменьшается и в точке оптимума она равна нулю.
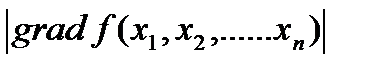 =0.
=0.
2. По значениям параметров оптимизации. Их значения в соседних точках отличаются на небольшую, наперед заданную величину.
Одним из наиболее используемых градиентных методов, является метод наискорейшего спуска.
Рассмотрим алгоритм на примере нахождения минимального значения функции 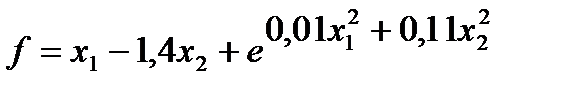 .
.
1. Находятся выражения частных производных функции по каждой переменной
 ,
,
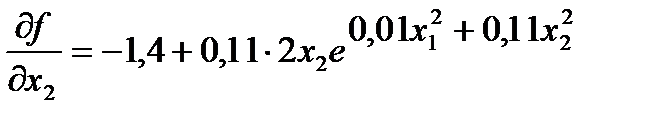 .
.
2. Определяются исходные данные:
Начальные значения переменных 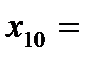 1,
1, 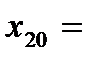 1.
1.
Величина рабочего шага 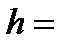 2.
2.
Точность решения 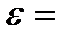 0, 1.
0, 1.
3. Выполняется рабочий шаг и вычисляются новые значения переменных по ранее приведенной формуле
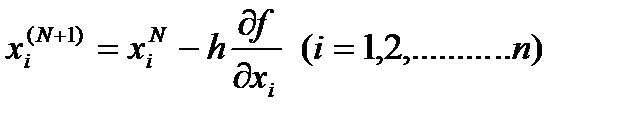 .
.
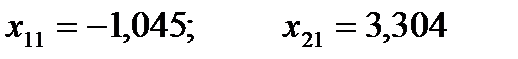
4. Для этих значений вычисляются значение функции

5. Вычисляется значение функции при начальных приближениях переменных
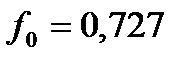
6. Так как значение функции уменьшилось после рабочего шага, то проверяется достигнутая точность нахождения минимума функции по величине скорости уменьшения функции, т.е. модулю градиента.

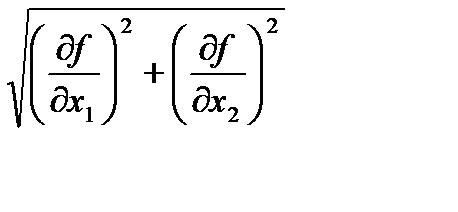
Эта величина будет равна 1, 396, что еще больше заданной точности.
7. Выполняется новый рабочий шаг той же величины получают новые значения неизвестных и значения функции.
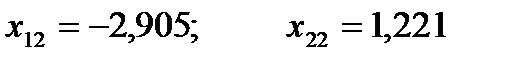
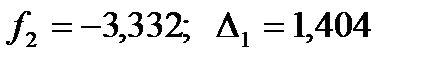
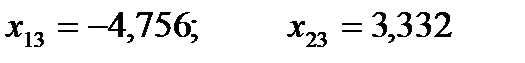

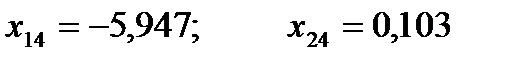
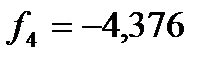
8. Произошло возрастание функции на четвертом шаге, поэтому длина шага делится пополам и вновь вычисляются значения переменных при этом шаге.
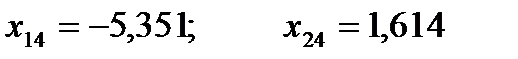
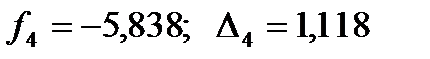
9. Происходит возврат к первоначальному шагу длиной 2 и продолжаются вычисления. Аналогичные ситуации возникают на 6, 8, 10, 12, 13, 15 и 16 шагах, т.е. на этих рабочих шагах выполняются дополнительные шаги с уменьшенными величинами шага. Причем на 10 шаге шаг уменьшался до 0, 5.
10. Окончательные результаты решения задачи.
 ;
;  . Всего выполнено 16 рабочих шагов.
. Всего выполнено 16 рабочих шагов.
|
|