Задание на контрольную работу. По курсу “Основы математического моделирования” выполняется одна контрольная работа

По курсу “Основы математического моделирования” выполняется одна контрольная работа. Каждое задание имеет 25 вариантов. Вариант задания выбирается по номеру в списке группы.

Контрольная работа включает в себя _ отдельных заданий:

1. Для матрицы из таблицы №1 приложения вычислить определитель, обратную матрицу, решить систему алгебраических уравнений методом Крамера и с помощью обратной матрицы.

2. Для полинома, коэффициенты которого заданы в таблице №2 приложения, найти вектор значений его в точках, заданных вектором аргумента, построить график изменения значений полинома. Найти все корни полинома.

3. Решить дифференциальное уравнение второго порядка, построить график переходного процесса и фазовый портрет.

4. Решить систему дифференциальных уравнений первого порядка

5. Вычислить определенный интеграл с использованием любого метода, реализованного в MatLab. Задание взять из таблицы № 5.

6. Решить дифференциальное уравнение в частных производных (параболическое) с использованием солвера построить график. Задание взять из таблицы № 6.

7. Задание взять из таблицы № 7.

Задание 1. (таблица №1)

clc;

A=[2, 4, 6, 1; 3, 76, 12, 45; -2, 5, -67, 12; 3, 4, 6, 9];

disp(A);

b=[4 7 12 89]';

disp(b);

d=det(A);

if d==0

disp('определитель матрицы а равен нулю');

break;

end

%Решение системы алгебраических уравнений методом Крамера

A1=[b, A(:, 2), A(:, 3), A(:, 4)];

A2=[A(:, 1), b, A(:, 3), A(:, 4)];

A3=[A(:, 1), A(:, 2), b, A(:, 4)];

A4=[A(:, 1), A(:, 2), A(:, 3), b];

x(1)=det(A1)/d;

x(2)=det(A2)/d;

x(3)=det(A3)/d;

x(4)=det(A4)/d;

x_k=x'; %Вектор решения, методом Крамера

Ao=inv(A); %Обратная матрица

x_o=Ao*b; %Вектор решения, полученный с обратной матрицей

x_r=A\b; %Вектор решения, полученный делением матриц

disp('Результаты решения системы уравнений');

disp(' x_k x_o x_r');

fprintf('| %5.2f | %5.2f | %5.2f |\n'...

, x_k, x_o, x_r);

Результаты решения системы уравнений

x_k x_o x_r

| 6.56 | -6.12 | 0.92 |

| 9.80 | 6.56 | -6.12 |

| 0.92 | 9.80 | 6.56 |

| -6.12 | 0.92 | 9.80 |

Задание 2. (таблица №2)

Одним из математических объектов, поддерживаемых в MatLab, является полином. Он представляется в системе вектором своих коэффициентов, начиная с коэффициента при старшей степени:

> > p=[2 4 -3 1];

Это запись полинома 2x³ + 4x² – 3x +1. Для полиномов реализовано большое количество функций, некоторые из которых приведены ниже:

%задание 2

clc; %

p=[2 4 -3 1]; %коэффициенты полинома

q=roots(p); %определение корней полинома

disp('корни полинома');

disp(q);

x=linspace(-10, 10); %вектор значений аргумента

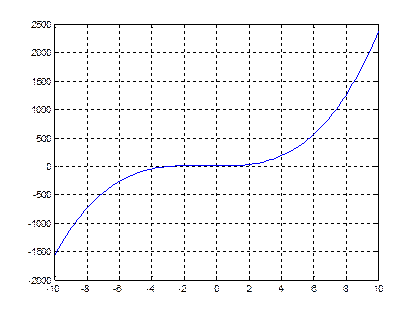
y=polyval(p, x); %значения полинома в точках ветора х

plot(x, y, '-')%график

grid on

корни полинома

-2.6399

0.3200 + 0.2950i

0.3200 - 0.2950i

Задание 3. (таблица №3)

function primer3

clc; %

clear all; %

%global m h c

m=5;

h=0.8;

c=20;

F=10;

x0=[0; 0]; %Начальные условия

Stime=[0 20]; %Интервал интегрирования

%------------Задание управляющей структуры--------------

options=odeset('RelTol', 1e-4);

%------------Вызов солвера-----------------------------

[t, x]=ode15s(@oscil, Stime, x0, options, F, c, h, m);

%------------Вывод графиков----------------------------

figure(1)

subplot (2, 1, 1); plot(t, x(:, 1));

grid on

set(gca, 'FontName', 'Arial Cyr', 'FontSize', 10);

title('Смещение')

xlabel('Время t')

ylabel('X')

subplot (2, 1, 2); plot(t, x(:, 2));

grid on

set(gca, 'FontName', 'Arial Cyr', 'FontSize', 10);

title('Скорость смещения')

xlabel('Время t')

ylabel('dX/dt')

figure(2)

plot(x(:, 1), x(:, 2));

grid on

set(gca, 'FontName', 'Arial Cyr', 'FontSize', 10);

title('Фазовый портрет осцилятора')

xlabel('X')

ylabel('dX/dt')

function dx=oscil(t, x, F, c, h, m)

%global m h c

dx=zeros(2, 1);

wp=2; %

dx(1)=x(2); %

dx(2)=-2*h/m*x(2)-c/m*x(1)+F*sin(wp*t); %

% dx(2)=x(1); %

% dx(1)=-2*h/m*x(2)-c/m*x(1)+F*sin(wp*t); %

Задание 4. (таблица №1)

> > A=[-2, -4, 3, 1; -1, -5, -7, -3; -10, -2, -4, 4; -1, 1, -1, -1];

> > q=eig(A)% Спектр матрицы А

q =

-10.1531

-0.2791 + 7.0321i

-0.2791 - 7.0321i

-1.2886

> > Ind_gest=max(real(abs(q)))/min(real(abs(q)))

Ind_gest =

a. Показатель жесткости системы дифференциальных уравнений

Как видно из полученных результатов спектр собственной матрицы системы дифференциальных уравнений лежит в левой части комплексной плоскости, а значит, система дифференциальных уравнений может быть решена численными методами. По значению показателя жесткости можно сделать вывод, что исследуемая система жесткой не является и можно использовать «солверы» оde 45 и ode 23.

function primer4

%primer4

clc;

clear all;

global A b

%Описание объекта дано в виде: dX/dt=A*X+b*u

%Собственный оператор объекта

A=[-2, -4, 3, 1; -1, -5, -7, -3; -10, -2, -4, 4; -1, 1, -1, -1];

%Матрица внешних воздействий

b=[4 7 12 89]';

%------Формирование условий обращения к солверу------------

x0=[0; 0; 0; 0]; %Начальные условия

Stime=[0 5]; %Интервал интегрирования

%------------Задание управляющей структуры--------------

options=odeset('RelTol', 1e-4);

%------------Вызов солвера-----------------------------

[t, x]=ode45(@SistODE, Stime, x0, options);

ppr(t, x); %

%--------------------------------------------------------

%Формирование системы дифференциальных уравнений

function dx=SistODE(t, x)

global A b

w=20.5;

Am=1.5;

u=Am*sin(w*t);

dx=zeros(4, 1);

dx=A*x+b*u;

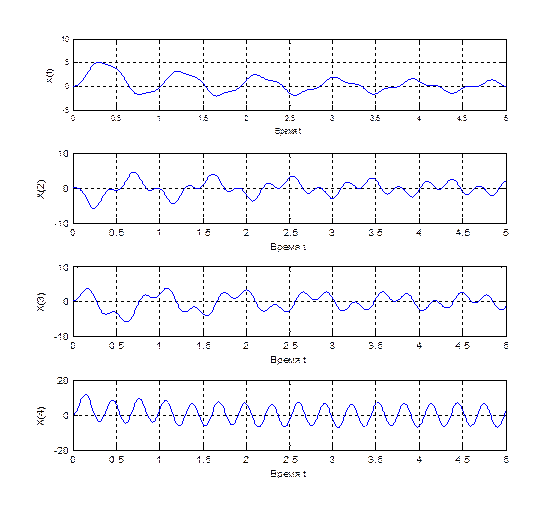
%------------Вывод графиков----------------------------

function ppr(t, x)

set(gca, 'FontName', 'Arial Cyr', 'FontSize', 8);

subplot (4, 1, 1); plot(t, x(:, 1));

set(gca, 'FontName', 'Arial Cyr', 'FontSize', 6);

grid on

xlabel('Время t')

ylabel('X(1)')

subplot (4, 1, 2); plot(t, x(:, 2));

set(gca, 'FontName', 'Arial Cyr', 'FontSize', 8);

grid on

xlabel('Время t')

ylabel('X(2)')

subplot (4, 1, 3); plot(t, x(:, 3));

set(gca, 'FontName', 'Arial Cyr', 'FontSize', 8);

grid on

xlabel('Время t')

ylabel('X(3)')

subplot (4, 1, 4); plot(t, x(:, 4));

set(gca, 'FontName', 'Arial Cyr', 'FontSize', 8);

grid on

xlabel('Время t')

ylabel('X(4)')

Задание 5 (таблица №4)

function primer5

%primer5

clc;

clear all;

format long; %" Длиная запись"

Tol=0.0025; %Точность расчета

a=5; %Нижний предел интегрирования

b=15; %Верхний предел интегрирования

h=0.001; %Шаг интегрирования для метода трапеций

x=a: h: b; %Вектор значений аргумента

Y=Fun(x); %Обращение к подынтегральной функции

Rez_trap=trapz(x, Y); %Результат расчета по методу трапеций

%Вычисление интеграла по методу Симпсона

% с заданной точностью

Rez_Sim=quad(@Fun, a, b, Tol); %Результат расчета по методу Симпсона

disp('Сравнение результатов интегрирования методом');

disp(' трапеций Симпсона ')

fprintf('| %10.8f | %10.8f |\n', Rez_trap, Rez_Sim);

function z=Fun(x)

%Подинтегральная функция

%z=(1.6*x-2.7)./(1.5*x.^3+3.9);

z=sqrt(2*x-1);

Сравнение результатов интегрирования методом

трапеций Симпсона

| 43.05659312 | 43.05659035 |

Задание 6 (таблица №5)

Решить параболическое уравнение в частных производных (PDE) с использованием встроенного «солвера» в системе MatLab. Уравнения в частных производных имеют вид:

Рассмотрим пример:

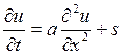
Граничные условия:

Начальные условия: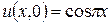

.

function primer6

clc;

clear all;

global a

m = 0; %коэффициент

a=10; %

x = linspace(0, 1, 20); %вектор значений координаты

t = linspace(0, 2, 5); %вектор значений времени

%

%pdepe - солвер для решения параболических уравнений в matlab

sol = pdepe(m, @pdex1pde, @pdex1ic, @pdex1bc, x, t);

u = sol(:,:, 1); %матрица результата решения

[nr nc]=size(u); %размер матрицы u

%

figure(1)

surf(x, t, u)

title('Numerical solution computed with 20 mesh points.')

xlabel('координата x')

ylabel('время t')

%

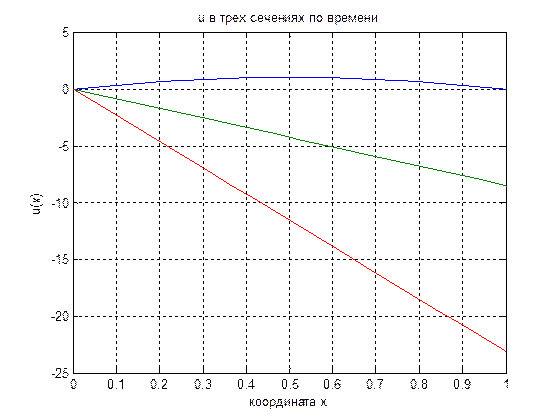
figure(2)

plot(x, u(1,:), x, u(3,:), x, u(nr,:)); %

title('u в трех сечениях по времени');

xlabel('координата x');

ylabel('u(x)');

grid on

% --------------------------------------------------------------

function [c, f, s] = pdex1pde(x, t, u, DuDx)

%коэффициенты уравнения

global a

c = 1/a^2; %

f = DuDx; %

s = 0; %

% --------------------------------------------------------------

function u0 = pdex1ic(x)

%начальное условие

u0 = sin(pi*x);

% --------------------------------------------------------------

function [pl, ql, pr, qr] = pdex1bc(xl, ul, xr, ur, t)

%граничное условие

pl = ul; %

ql = 0; %

pr = pi * exp(t); %

qr = 1; %

Задание 7. (таблица №6)