
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Families of circles
|
|
A great deal can be done toward the visualization of linear transformation by the introduction of certain families of circles which may be thought of as coordinate lines in a circular coordinate system.
Consider a linear transformation of the form
w=k 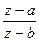 .
.
Here z=a corresponds to w=0 and z=b to w=∞. It follows that the straight lines through the origin of the w-plane are images of the circles through a and b. On the other hand, the concentric circles about the origin |w|=ρ correspond to circles with the equation | 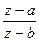 |= ρ.
|= ρ.
These are the circles of Apollonius with limit points a and b. By their equation they are the loci of points whose distances from a and b have a constant ratio.
Denote by C1 the circles through a, b and by C2 the circles of Apollonius with these limit points. The configuration formed by all the circles C1 and C2 will be referred to as the circular net or the Steiner circles determined by a and b. It has many interesting properties of which we shall list a few:
1. There is exactly one C1 and one C2 through each point in this plane with the exception of the limit points.
2. Every C1 meets every C2 under right angles.
3. Reflection in a C1 transforms every C2 into itself and every C1 into another C1. Reflection in a C2 transforms every C1 into itself and every C2 into another C2.
4. The limit points are symmetric with respect to each C2 but not with respect to any other circle.
These properties are all trivial when the limit points are 0 and ∞, i.e. when the C1 are lines through the origin and the C2 concentric circles. Since the properties are invariant under linear transformation, they must continue to hold in the general case.
If a transformation w=T2 carries a, b into a’, b’, it can be written in the form
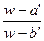 =k
=k 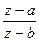 .
.
It is clear that T transforms the circles C1 and C2 into circles C 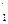 and C2 with the limit points a’, b’.
and C2 with the limit points a’, b’.
The situation is particularly simple is a’=a, b’=b. Then a, b are said to be fixed points of T and it is convenient to represent z and Tz in the same plane. Under these circumstances, the whole circular net will be mapped upon itself. The value of k serves to identify the image circles C 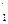 and C
and C  . Indeed, with appropriate orientations C1 forms the angle arg k with its image C
. Indeed, with appropriate orientations C1 forms the angle arg k with its image C 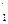 , and the quotient of the constant ratios |z-a|/|z-b| on C
, and the quotient of the constant ratios |z-a|/|z-b| on C  and C2 is |k|.
and C2 is |k|.
The special cases in which all C1 or all C2 are mapped upon themselves are particularly important. We have C 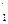 =C1 for all C1 if k > 0 (if k > 0, the circles are still the same, but the orientation is reversed). The transformation is then said to be hyperbolic. When k increases, the points Tz, z≠ a, b will flow along the circles C1 toward b. The consideration of this flow provides a very clear picture of a hyperbolic transformation.
=C1 for all C1 if k > 0 (if k > 0, the circles are still the same, but the orientation is reversed). The transformation is then said to be hyperbolic. When k increases, the points Tz, z≠ a, b will flow along the circles C1 toward b. The consideration of this flow provides a very clear picture of a hyperbolic transformation.
The case C  =C2 occurs when |k|=1. Transformations with this property are called elliptic. When arg k varies, the points Tz move along the circles C2. The corresponding flow circulates about a and b in different directions.
=C2 occurs when |k|=1. Transformations with this property are called elliptic. When arg k varies, the points Tz move along the circles C2. The corresponding flow circulates about a and b in different directions.
The general linear transformation with two fixed points is the product of a hyperbolic and an elliptic transformation with the same fixed points.
The fixed points of a linear transformation are found by solving the equation
z= 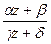 .
.
In general this is a quadratic equation with two roots; if γ =0, one of the fixed points is ∞. It may happen, however, that the roots coincide. A linear transformation with coinciding fixed points is said to be parabolic. The condition for this is (α -δ)2=4β γ.
*Source: L.Ahlfors Complex Analysis, p.31-33.
|
|