Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Pre-reading tasks. 1. General comprehension questions:
|
|
1. General comprehension questions:
1) What kind of number is called complex?
2) Can it be represented geometrically? In what form? Why is it useful?
3) What operations can be done with complex numbers?
A list of words you might need for the answer:
Field, subfield, imaginary unit, argument, complex plane, conjugate, addition, subtraction, multiplication, division, to obey the rule/law
2. Learn to read the following formulas:
1) x2=c
x squared is equal to c;
2) 
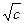
the square root of c;
3) -
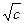
minus square root of c;
4) x2+2bx+c=0
x squared plus two bx plus c is equal to 0;
5) (a+b)2=b2-c
a plus b in parenthes, all to the second power, is equal to b squared minus c.
or: parenthesis, a plus b, close parenthesis, to the second power is equal to b squared minus c;
6) b≥ a
b is greater than or equal to a;
7) b< a
b is less than a;
8) (-a)(-b)=ab
minus a multiplied by minus b is equal to ab;
9) b≠ 0
b is not equal to 0;
10) α β =(α +bi)(c+di)=ac-bd+(ad+bc)i
α times β is equal to α +bi in parentheses, all multiplied by c+di, in parentheses, is equal to ac minus bd plus parenthesis ad plus bc close parentheses, multiplied by i;
11) γ =α /β
γ is equal to α divided by β; or: γ is equal to α over β;
12) |α |² +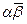 
+ 
+|β |2
modulus of α squared plus α β barred plus α barred β plus modulus of β squared;
13) |α 1…α n|
modulus of α sub 1 and so on α sub n;
14) |α n|=|α |n
modulus of α to the power n is equal to modulus of α all to the power n.
Read Text 1 aloud with the formulas:
Text 1.
The complex numbers are the field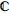 
of numbers of the form 
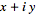, where 
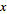and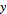 
are real numbers and i is the imaginary unit equal to the square root of 
, 
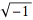. When a single letter 
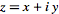is used to denote a complex number, it is sometimes called an " affix." In component notation, 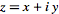can be written 
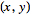. The field of complex numbers includes the field of real numbers as a subfield.
Complex numbers are useful abstract quantities that can be used in calculations and result in physically meaningful solutions. However, recognition of this fact is one that took a long time for mathematicians to accept. For example, John Wallis wrote, " These Imaginary Quantities (as they are commonly called) arising from the Supposed Root of a Negative Square (when they happen) are reputed to imply that the Case proposed is Impossible" (Wells 1986, p. 22).
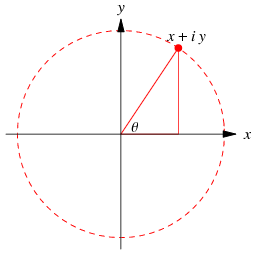
Through the Euler formula, a complex number
|
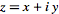
| (1) |
may be written in " phasor" form
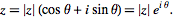
| (2) |
Here,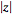 
is known as the complex modulus (or sometimes the complex norm) and 
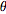is known as the complex argument or phase. The plot above shows what is known as an Argand diagram of the point 
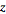, where the dashed circle represents the complex modulus 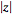of 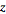and the angle 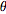represents its complex argument. Historically, the geometric representation of a complex number as simply a point in the plane was important because it made the whole idea of a complex number more acceptable. In particular, " imaginary" numbers became accepted partly through their visualization.
Unlike real numbers, complex numbers do not have a natural ordering, so there is no analog of complex-valued inequalities. This property is not so surprising however when they are viewed as being elements in the complex plane, since points in a plane also lack a natural ordering.
The absolute square of 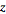is defined by 
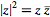, with 
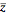the complex conjugate, and the argument may be computed from
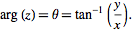
| (3) |
The real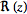 
and imaginary parts 
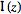are given by
|
| 
| 
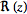
| (4) |
|
|
| 
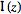
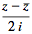
| (5) |
|
| 
| (6) |
|
|
| 
| (7) |
de Moivre's identity relates powers of complex numbers for real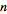 
by
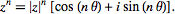
| (8) |
A power of complex number 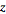to a positive integer exponent 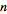can be written in closed form as
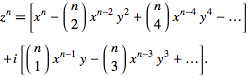
| (9) |
The first few are explicitly
|
| 
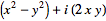
| (10) |
|
| 
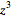
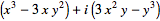
| (11) |
|
| 
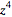
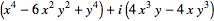
| (12) |
|
| 
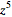
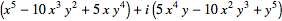
| (13) |
(Abramowitz and Stegun 1972).
Complex addition
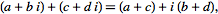
| (14) |
complex subtraction
| (15) |
complex multiplication
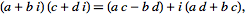
| (16) |
and complex division
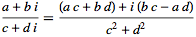
| (17) |
can also be defined for complex numbers. Complex numbers may also be taken to complex powers. For example, complex exponentiation obeys
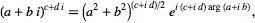
| (18) |
where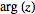 
is the complex argument.
*Source: Weisstein, Eric W. " Complex Number." From MathWorld --A Wolfram Web Resource. https://mathworld.wolfram.com/ComplexNumber.html
|
|