Примеры предгильбертовых пространств

Пример 11.1. Линейное пространство R^m со скалярным произведением

< х, у > =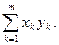

Пример 11.2. Линейное пространство l ₂ со скалярным произведением

< х, у > = ,

где х = х₁, х₂,... и у = у₁, у₂... любые элементы множества l ₂.

Пример 11.3. Линейное пространство C [ a, b ] со скалярным произведением

< х, у > = 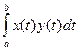" х, уÎ C [ a, b ].

Проверка аксиом скалярного произведения не представляет сложности. Проведите ее самостоятельно.

Лемма 11.1. В любом предгильбертовом пространстве А справедливо неравенство

, (11.1)

которое называется неравенством Коши-Буняковского.

3Если у = q, то справедливость неравенства очевидна. Пусть у ¹ q. Исходя из системы аксиом скалярного произведения имеем неравенство

< х - lу, х - lу > = < х, х > - 2 l< х, у > + l² < у, у > ³ 0,

которое справедливо для произвольного числа l. Подставив в нее l =< х, у> ¤< у, у> получим неравенство Коши-Буняковского. 4

Лемма 11.2. В любом предгильбертовом пространстве формула

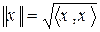(11.2)

определяет норму.

Доказательство леммы сводится к проверке аксиом нормы. Это не вызывает трудностей и поэтому проведите проверку самостоятельно.

Итог. На основании леммы 11.2 неравенство Коши-Буняковского имеет вид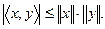

Таким образом, предгильбертово пространство является нормированным пространством и поэтому для него имеют место все определения и утверждения для нормированным пространств.

Определение 11.2. Полное предгильбертово пространство относительно нормы (11.2) называется гильбертовым пространством.

Примерами гильбертовых пространств являются пространства в примерах 11.1 и 11.2. Предгильбертово пространство в примере 3 не является полным относительно нормы (11.2) и поэтому не является гильбертовым.