
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод Рунге-Кутты
|
|
Метод Рунге-Кутты позволяет строить схемы решения ОДУ различного порядка точности. Основная идея метода состоит в том, что ищется (по определенному алгоритму) несколько направлений касательных в промежуточных точках, выбранных на отрезке расчета, и затем, придав каждому из направлений индивидуальный вес, высчитывают усредненное направление касательной из левой точки отрезка вычисления. Методы Рунге-Кутты отличаются различием в количестве, назначении промежуточных расчетных точек и шкалой весовых коэффициентов для расчетных направлений. Ниже рассматривается наиболее широкоприменяемый чертырехшаговый метод Рунге-Кутты. Анализируя ранее приведенные методы, заметим, что метод Эйлера – одношаговый, т.е. приближение получают за одно вычисление. Метод срединной точки – двухшаговый, а метод с пересчетом – трехшаговый. Таким образом, с понятием «многошаговый расчет» мы фактически уже знакомы.
Если решается ОДУ 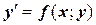 при начальных условиях
при начальных условиях 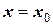 ;
; 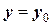 и точным его решением будет функция
и точным его решением будет функция  , то, применяя разностный метод, ищут очередную точку
, то, применяя разностный метод, ищут очередную точку 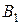 , лежащую на кривой функции
, лежащую на кривой функции  при
при 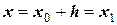 в виде какого-то приближения. Первое приближение – это точка
в виде какого-то приближения. Первое приближение – это точка 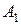 , получаемая методом Эйлера и имеющая ординату
, получаемая методом Эйлера и имеющая ординату 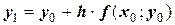 . Тогда можно обратить внимание на то, что
. Тогда можно обратить внимание на то, что 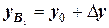 , а ордината точки
, а ордината точки 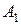
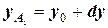 , т.е. точное приращение функции заменяется его дифференциалом (рисунок 30). Как известно,
, т.е. точное приращение функции заменяется его дифференциалом (рисунок 30). Как известно, 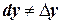 , но
, но 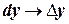 при
при 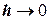 . Метод Рунге-Кутты состоит в построении специального алгоритма – такого, чтобы величина
. Метод Рунге-Кутты состоит в построении специального алгоритма – такого, чтобы величина 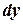 возможно максимально совпала с
возможно максимально совпала с 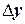 .
.
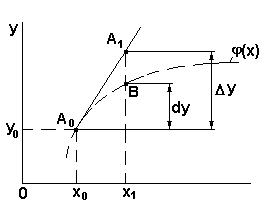
Рисунок 30 - К обоснованию метода Рунге-Кутты
Рассмотрим четырехшаговый метод Ругнге-Кутты, также иногда называемый схемой четвертого порядка точности. Его геометрическая трактовка представлена на рисунке 31. Предположим, имеется ОДУ 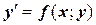 при начальных условиях
при начальных условиях 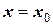 ;
; 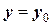 , что соответствует точке
, что соответствует точке 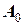 . Найдем очередную точку приближения к искомой функции
. Найдем очередную точку приближения к искомой функции 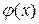 для
для 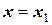 . Разделим участок
. Разделим участок 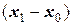 пополам. Дальнейшие процедуры рассматриваем пошагово.
пополам. Дальнейшие процедуры рассматриваем пошагово.
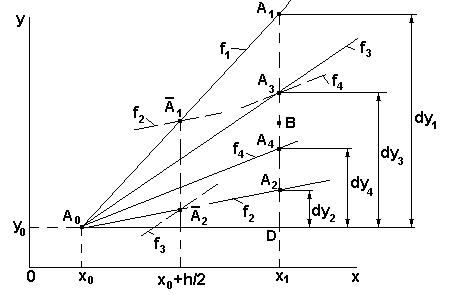
Рисунок 31 - Геометрическая трактовка алгоритма метода Рунге-Кутты
1) Первый шаг метода Рунге-Кутты заключается в следующем. Находим точку 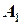 построением касательной
построением касательной 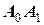 с тангенсом угла наклона
с тангенсом угла наклона 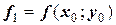 (метод Эйлера). Обозначим приращение
(метод Эйлера). Обозначим приращение 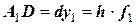 . По методу срединной точки находим точку
. По методу срединной точки находим точку 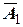 и ее ординату
и ее ординату
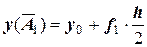 .
.
Для этой точки рассчитывается новое направление касательной
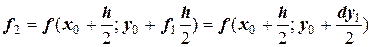 .
.
Первый шаг завершается получением 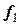 и
и 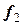 .
.
2) Второй шаг заключается в построении из точки 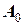 второй касательной с тангенсом угла наклона
второй касательной с тангенсом угла наклона 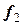 и получении точки
и получении точки 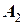 . Определяют приращение для этой точки
. Определяют приращение для этой точки 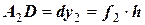 . На этой касательной рассчитывают положение срединной точки
. На этой касательной рассчитывают положение срединной точки 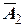 :
:
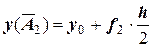
и строят через нее очередную касательную
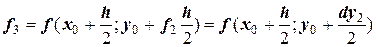 .
.
Таким образом, становятся известны уже три угловых коэффициента 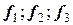 .
.
3) Третий шаг заключается в построении опять из точки 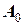 касательной линии с тангенсом угла наклона
касательной линии с тангенсом угла наклона 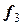 . В результате получают третье приближение
. В результате получают третье приближение 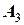 , а ее приращение равно
, а ее приращение равно 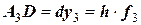 .
.
Для этой точки рассчитывают направление четвертой касательной:
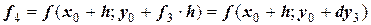 .
.
4) Четвертый шаг заключается в построении из точки 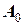 касательной (уже четвертой) с тангенсом угла наклона
касательной (уже четвертой) с тангенсом угла наклона 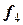 и получении четвертой точки приближения
и получении четвертой точки приближения 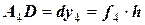 .
.
В результате получены четыре точки 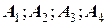 (равно как и дифференциалы
(равно как и дифференциалы 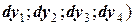 , но это только некоторые приближения к конечной точке
, но это только некоторые приближения к конечной точке 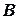 . Заключительным шагом является расчет положения точки
. Заключительным шагом является расчет положения точки 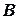 , которая и принимается за следующее приближение к функции
, которая и принимается за следующее приближение к функции  при
при 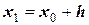 . Приближение
. Приближение 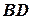 рассчитывают как средневзвешенное
рассчитывают как средневзвешенное 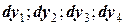 , причем с разичными весовыми коэффициентами:
, причем с разичными весовыми коэффициентами:
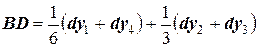 .
.
Иначе, доля внутренних приближений принимается более значимой по сравнению с приближениями крайними.
В общем виде метод Рунге-Кутты по схеме четвертого порядка записывается следующим образом:
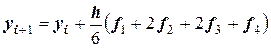 ,
,
где 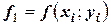 ;
;
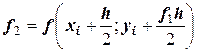 ;
;
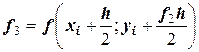 ;
;
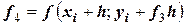 .
.
Задача 24. Решить ОДУ вида 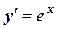 для участка
для участка 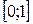 при начальных условиях
при начальных условиях 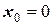 ;
; 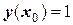 ;
; 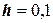 . Решение получить методом Эйлера и методом Рунге-Кутты.
. Решение получить методом Эйлера и методом Рунге-Кутты.
Решение. В данном случае мы можем получить и точное решение этого уравнения. Действительно:
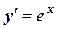 ;
; 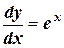 ;
; 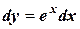 ;
;
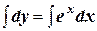 ;
;
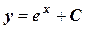 .
.
Очевидно, что 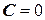 . Тогда
. Тогда
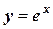 .
.
Теперь запишем решение методом Эйлера:
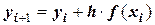
или 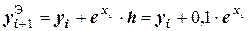 .
.
Это общее уравнение приближенного решения. Для метода Рунге-Кутты запишем:
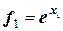 ;
;
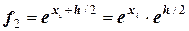 ;
;
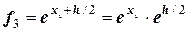 ;
;
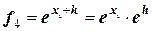 ;
;
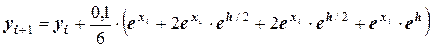 ;
;
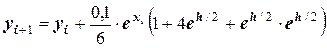 .
.
Подставив значения постоянных величин, получим:
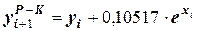 .
.
Составим расчетную таблицу 28.
Таблица 28 - Расчетная таблица решения уравнения 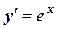
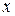
| 0, 1 | 0, 2 | 0, 3 | 0, 4 | 0, 5 | 0, 6 | 0, 7 | 0, 8 | 0, 9 | 1, 0 | |
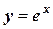
| 1, 105 | 1, 221 | 1, 350 | 1, 492 | 1, 649 | 1, 825 | 2, 014 | 2, 224 | 2, 460 | 2, 718 | |
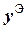
| 1, 100 | 1, 211 | 1, 333 | 1, 468 | 1, 617 | 1, 782 | 1, 964 | 2, 165 | 2, 388 | 2, 634 | |
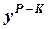
| 1, 112 | 1, 245 | 1, 387 | 1, 544 | 1, 717 | 1, 908 | 2, 120 | 2, 354 | 2, 613 | 2, 899 |
Сравнивая результаты приближенных вычислений с точными данными, видим, что методы Эйлера и Рунге-Кутты соотносятся следующим образом:
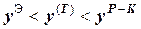 .
.
|
|