
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Атомные кристаллы
|
|
Атомные (по типу полярности – гомеополярные) кристаллы образуются за счет ковалентной связи. Она предопределена электростатическим и обменным взаимодействием. Понимание природы ковалентной связи может быть достигнуто только с помощью квантово-механических представлений, которые учитывают волновые свойства электрона. При ковалентной связи соседние атомы образуют общие электронные оболочки, обмениваясь электронами. Как следует из квантово-механических расчетов, при образовании общих электронных оболочек потенциальная энергия системы уменьшается за счет так называемых обменных эффектов. Уменьшение энергии эквивалентно возникновению сил притяжения.
Механизм возникновения обменного взаимодействия рассмотрим на примере образования молекулы водорода, в которой два электрона движутся в поле двух ядер (рис. 2.2).
| Рис.2.2. Схематическое изображение молекулы водорода: а, b – ядра; 1, 2 – электроны |
Потенциальная энергия взаимодействия между двумя атомами состоит из двух частей: из энергии взаимодействия ядер и из энергии электронов, которая зависит от расстояния между двумя ядрами R:
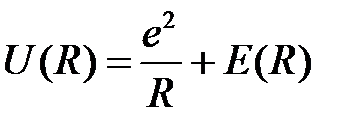 . (2.1)
. (2.1)
Для нахождения собственных функций и собственных значений энергии такой системы необходимо решить стационарное уравнение Шредингера:
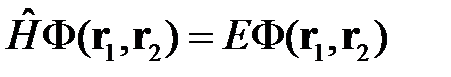 . (2.2)
. (2.2)
Гамильтониан молекулы водорода можно предоставить следующим образом:
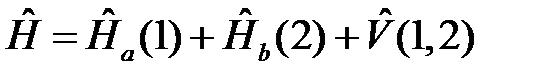 , (2.3)
, (2.3)
где 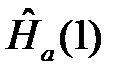 отвечает движению первого электрона (1) вокруг ядра (а)
отвечает движению первого электрона (1) вокруг ядра (а)
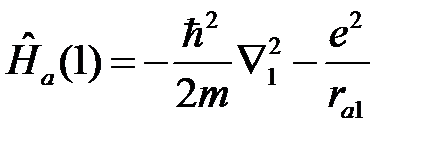 , (2.4)
, (2.4)
 отвечает движению второго электрона (2) вокруг ядра (b)
отвечает движению второго электрона (2) вокруг ядра (b)
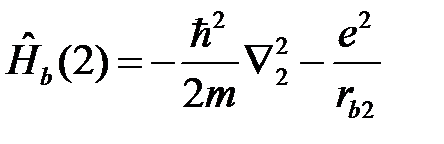 , (2.5)
, (2.5)
а 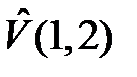 представляет энергию электростатического взаимодействия электронов с «чужими» ядрами и между собой
представляет энергию электростатического взаимодействия электронов с «чужими» ядрами и между собой
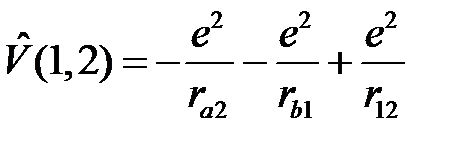 . (2.6)
. (2.6)
Точное решение уравнения Шредингера с гамильтонианом (2.3) провести невозможно. Воспользуемся методом возмущений. Сначала рассмотрим большие расстояния 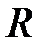 . Пусть первый электрон находится около ядра
. Пусть первый электрон находится около ядра  , а второй – около ядра
, а второй – около ядра  . Тогда величиной
. Тогда величиной 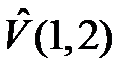 в (2.3) можно пренебречь и мы получим уравнение
в (2.3) можно пренебречь и мы получим уравнение
 . (2.7)
. (2.7)
В качестве начального приближения для волновой функции используем волновые функции невзаимодействующих атомов водорода:
 , (2.8)
, (2.8)
где 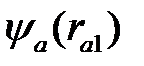 и
и 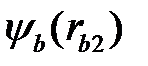 находятся из решения уравнений
находятся из решения уравнений
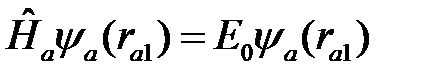 , (2.9)
, (2.9)
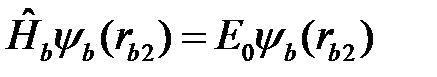 . (2.10)
. (2.10)
Соответствующее решению (2.8) значение энергии будет 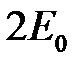 .
.
Если бы отсутствовало вырождение, то решение (2.8) и было бы нулевым приближением. В действительности, в этом случае мы имеем так называемое обменное вырождение. Очевидно, что кроме решения (2.8) возможно и такое решение, когда в первом атоме (а) находится второй электрон (2), а во втором атоме (b) – первый электрон (1). Гамильтониан будет иметь такой же вид, как и (2.3), только электроны поменяются местами (1«2). Решение будет иметь вид
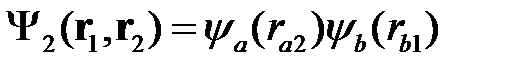 . (2.11)
. (2.11)
Таким образом, для больших 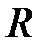 уравнение (2.2) имеет два решения (2.8) и (2.11), которые принадлежат энергии
уравнение (2.2) имеет два решения (2.8) и (2.11), которые принадлежат энергии 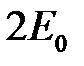 . При учете взаимодействия между атомами нулевое приближение к
. При учете взаимодействия между атомами нулевое приближение к 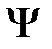 будет линейной комбинацией
будет линейной комбинацией 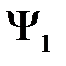 и
и  :
:
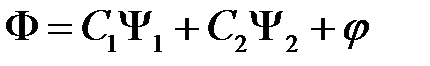 , (2.12)
, (2.12)
где 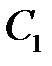 и
и 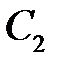 – коэффициенты, которые требуется определить, а
– коэффициенты, которые требуется определить, а 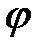 – малый добавок к нулевому приближению.
– малый добавок к нулевому приближению.
Энергию представим в виде
 , (2.13)
, (2.13)
где 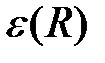 – добавок, который определяет изменение энергии электронов при сближении атомов.
– добавок, который определяет изменение энергии электронов при сближении атомов.
Подставляя (2.12) и (2.13) в (2.2) и пренебрегая малыми величинами  ,
,  ,
, 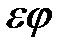 , получим
, получим
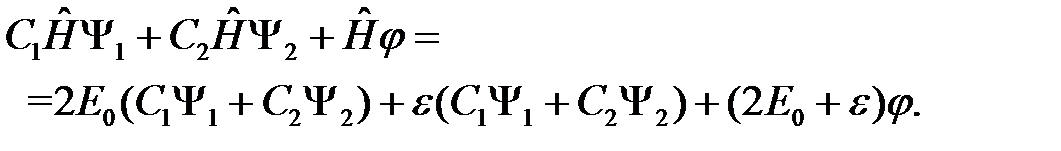 (2.14)
(2.14)
Воспользуемся (2.3) и последним выражением, но с учетом перестановки электронов. Тогда (2.14) приобретает вид
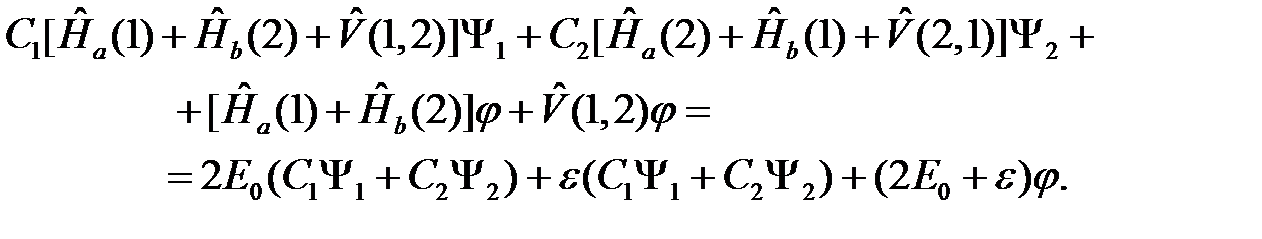 (2.15)
(2.15)
Подставим в (2.15) 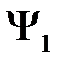 и
и  из (2.8) и (2.11) и пренебрежем малыми слагаемыми
из (2.8) и (2.11) и пренебрежем малыми слагаемыми 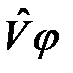 ,
,  . Получим
. Получим
 (2.16)
(2.16)
Это неоднородное уравнение для определения поправок к волновой функции 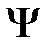 и к собственному значению энергии
и к собственному значению энергии  .
.
Неоднородное уравнение имеет решение в том случае, когда его правая часть ортогональна к решению  однородного уравнения (такое уравнение возникает, если правая часть в (2.16) равняется нулю). То есть должно выполняться условие
однородного уравнения (такое уравнение возникает, если правая часть в (2.16) равняется нулю). То есть должно выполняться условие
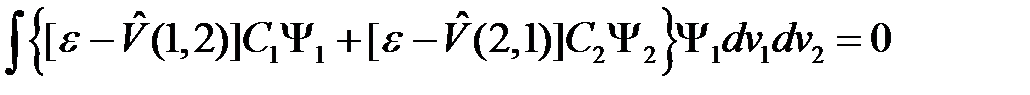 , (2.17)
, (2.17)
где 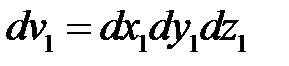 ,
, 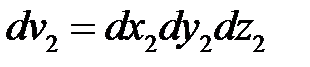 .
.
Аналогичным путем получим и второе уравнение (ортогональность к решению 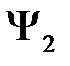 )
)
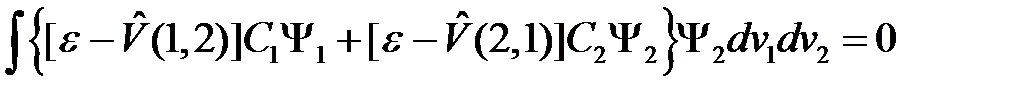 . (2.18)
. (2.18)
Введем следующие сокращенные обозначения
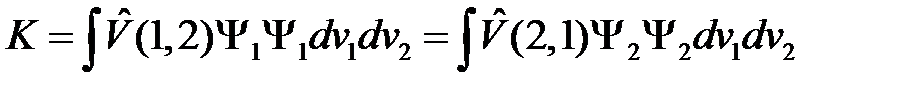 , (2.19)
, (2.19)
 . (2.20)
. (2.20)
Функции 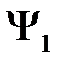 и
и 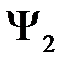 не ортогональны между собой, поэтому введем еще следующий интеграл
не ортогональны между собой, поэтому введем еще следующий интеграл
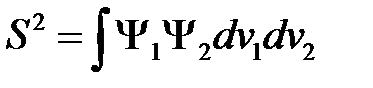 . (2.21)
. (2.21)
С помощью этих обозначений уравнения (2.17) и (2.18) запишутся следующим образом
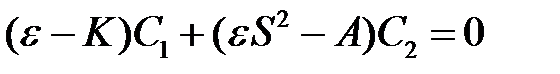 , (2.22)
, (2.22)
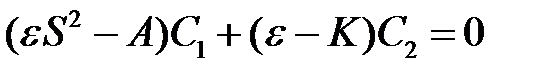 . (2.23)
. (2.23)
Из этих уравнений вначале получим уравнение для 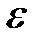 :
:
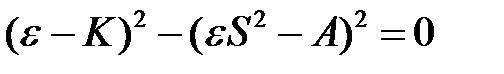 . (2.24)
. (2.24)
Оно имеет два корня
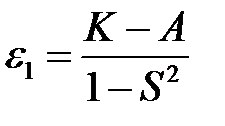 , (2.25)
, (2.25)
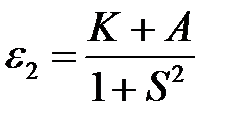 . (2.26)
. (2.26)
Подставляя эти значения в (2.22), найдем для 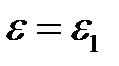
 (2.27)
(2.27)
и для 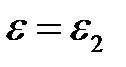
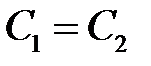 . (2.28)
. (2.28)
Следовательно, решения запишутся в таком виде:
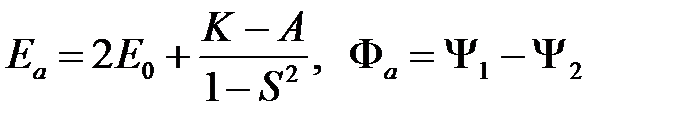 (2.29)
(2.29)
(антисимметричное решение) и
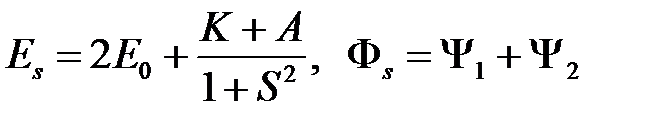 (2.30)
(2.30)
(симметричное решение).
Рассмотрим физический смысл интегралов 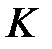 и
и 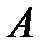 . Воспользовавшись (2.19), (2.6) и (2.11), получим
. Воспользовавшись (2.19), (2.6) и (2.11), получим
 . (2.31)
. (2.31)
Воспользуемся условиями нормировки  и
и 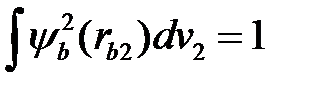 , обозначим среднюю плотность электронного заряда, который создается электроном (1) в атоме (а), через
, обозначим среднюю плотность электронного заряда, который создается электроном (1) в атоме (а), через 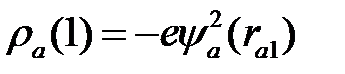 , электроном (2) в атоме (b) через
, электроном (2) в атоме (b) через 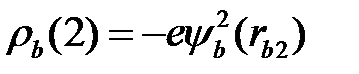 . В этом случае получим для
. В этом случае получим для 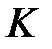 :
:
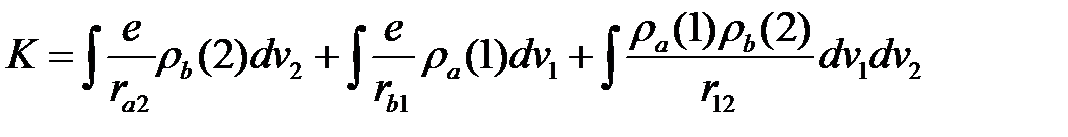 . (2.32)
. (2.32)
Первый интеграл является средней потенциальной энергией электрона (2) атома (b) в поле ядра (а), второй интеграл – та же самая величина для электрона (1) атома (а) в поле ядра (b) и третий интеграл – средняя потенциальная энергия электронов, которые находятся в разных атомах. Таким образом, 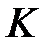 есть средняя энергия электростатического взаимодействия атомов
есть средняя энергия электростатического взаимодействия атомов  , кроме энергии взаимодействия ядер, которая вычисляется отдельно (2.1).
, кроме энергии взаимодействия ядер, которая вычисляется отдельно (2.1).
Интеграл (2.20) называют обменным интегралом. Обозначив обменную плотность
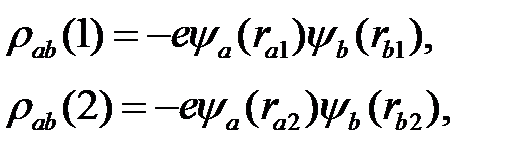 (2.33)
(2.33)
запишем 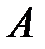 в виде
в виде
 . (2.34)
. (2.34)
Последнее слагаемое представляет обменную энергию, которой нет никаких аналогов в классической механике. Она обусловлена тем, что каждый из электронов может находиться частично около атома (a), частично – около (b).
Первые два слагаемых в правой части (2.34) представляют поправки к обменной энергии из-за не ортогональности волновых функций, собственно,
 . (2.35)
. (2.35)
При 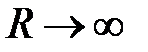 волновые функции
волновые функции 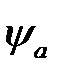 и
и 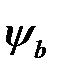 из-за экспоненциального уменьшение с ростом расстояния от ядер (a) и (b) слабо перекрываются, следовательно,
из-за экспоненциального уменьшение с ростом расстояния от ядер (a) и (b) слабо перекрываются, следовательно, 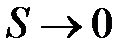 . Когда же
. Когда же 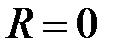 , ядра (a) и (b) совпадают. Тогда
, ядра (a) и (b) совпадают. Тогда 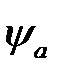 и
и 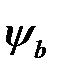 являются волновыми функциями один и того же атома водорода. В силу нормировки
являются волновыми функциями один и того же атома водорода. В силу нормировки 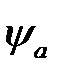 и
и 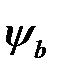 при
при 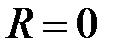
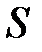 равняется 1. Следовательно,
равняется 1. Следовательно,
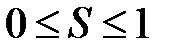 . (2.36)
. (2.36)
Интеграл  также изменяется в этих пределах.
также изменяется в этих пределах.
Воспользовавшись (2.1), (2.12) (2.29) и (2.30) и выполнив некоторые преобразования, получим
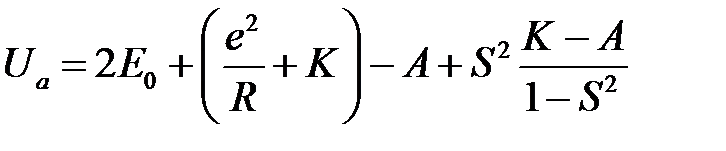 , (2.37)
, (2.37)
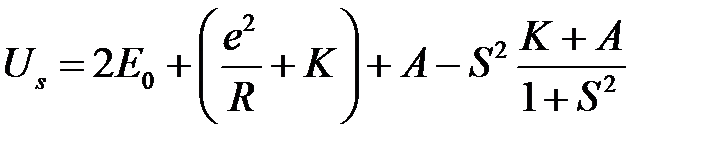 . (2.38)
. (2.38)
Члены  представляют среднюю кулоновскую энергию двух атомов водорода, которые находятся на расстоянии
представляют среднюю кулоновскую энергию двух атомов водорода, которые находятся на расстоянии 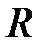 друг от друга,
друг от друга,  – обменная энергия. Последний член с
– обменная энергия. Последний член с  включает поправки на неортогональность волновых функций, которые были использованы в качестве нулевого приближения.
включает поправки на неортогональность волновых функций, которые были использованы в качестве нулевого приближения.
С помощью формул (2.32) и (2.34) может быть вычислена и кулоновская, и обменная энергия, если использовать для 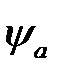 и
и 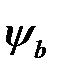 волновую функцию нормального состояния водорода:
волновую функцию нормального состояния водорода:
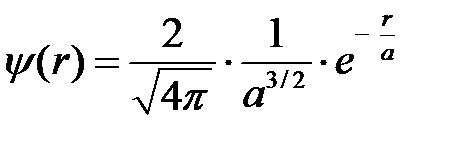 , (2.39)
, (2.39)
где  – расстояние электрона от ядра,
– расстояние электрона от ядра, 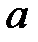 – радиус первой боровской орбиты.
– радиус первой боровской орбиты.
Интегралы 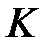 и
и  содержат волновые функции, которые принадлежат к разным атомам и каждая из этих функций экспоненциально уменьшается с расстоянием. Поэтому оба интеграла
содержат волновые функции, которые принадлежат к разным атомам и каждая из этих функций экспоненциально уменьшается с расстоянием. Поэтому оба интеграла 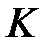 и
и  отличаются от нуля лишь потому, что волновые функции, а, следовательно, и электронные оболочки атомов перекрываются. В результате оба интеграла уменьшаются при увеличении расстояния между атомами, как
отличаются от нуля лишь потому, что волновые функции, а, следовательно, и электронные оболочки атомов перекрываются. В результате оба интеграла уменьшаются при увеличении расстояния между атомами, как 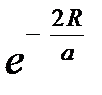 . На рис.2.3 приведена взаимная энергия атомов
. На рис.2.3 приведена взаимная энергия атомов 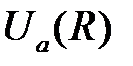 и
и 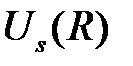 как функция расстояния между ними. Величина
как функция расстояния между ними. Величина 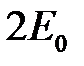 принята при отсчете энергии за 0.
принята при отсчете энергии за 0.
| Рис.2.3. Энергия симметричного и антисимметричного состояний |
Как видно из рисунка, для антисимметричного состояния 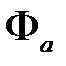 энергия
энергия 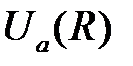 отвечает взаимному отталкиванию двух атомов водорода, и потому молекула
отвечает взаимному отталкиванию двух атомов водорода, и потому молекула  образоваться не может. Напротив, для симметричного состояния
образоваться не может. Напротив, для симметричного состояния  энергия
энергия 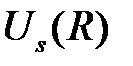 имеет минимум, в этом случае атомы водорода находятся на расстоянии
имеет минимум, в этом случае атомы водорода находятся на расстоянии 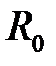 и образуют молекулу. Волновая функция
и образуют молекулу. Волновая функция  зависит только от координат. Полная волновая функция должна зависеть еще и от спинов электронов
зависит только от координат. Полная волновая функция должна зависеть еще и от спинов электронов 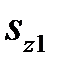 и
и  . Поскольку взаимодействием спинов с орбитальным движением и взаимодействием спинов между собой мы пренебрегли, то полная волновая функция должна быть произведением координатной функции
. Поскольку взаимодействием спинов с орбитальным движением и взаимодействием спинов между собой мы пренебрегли, то полная волновая функция должна быть произведением координатной функции  и спиновой
и спиновой 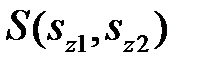 . Электроны подчиняются принципу Паули, поэтому волновая функция должна быть асимметричной относительно перестановки электронов. Мы имеем координатную функцию или симметричную
. Электроны подчиняются принципу Паули, поэтому волновая функция должна быть асимметричной относительно перестановки электронов. Мы имеем координатную функцию или симметричную  , или антисимметричную
, или антисимметричную 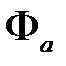 .
.
Полная волновая функция будет антисимметричной при симметричной координатной и антисимметричной спиновой, а также при антисимметричной координатной и симметричной спиновой.
Следовательно, два атома водорода, которые имеют электроны с противоположными спинами (синглетное состояние), притягиваются друг к другу. Атомы водорода, которые имеют электроны с параллельными спинами (триплетное состояние), отталкиваются.
Если атом вещества имеет несколько неспаренных электронов, то может возникнуть соответствующее число обменных связей. Например, в кристаллах с решеткой алмаза (рис.1.9, а) каждый атом связан с четырьмя ближайшими соседями.
Ковалентная связь образуется при перекрывании электронных оболочек, следовательно, она наблюдается при малых расстояниях между атомами. Причем плотность «электронного облака» увеличивается по направлениям, которые соединяют атомы, то есть электроны как бы втянуты в пространство между ядрами и своим полем обеспечивают их притяжение. Отсюда вытекает направленность и насыщаемость ковалентных связей: они действуют только по определенным направлениям и между определенным числом соседей.
Ковалентная связь преобладает в атомных кристаллах и по порядку величины приближается к ионной связи. Такие кристаллы имеют низкую сжимаемость и высокую твердость. В электрическом отношении они являются диэлектриками или полупроводниками.
К веществам с ковалентными связями относится:
– большинство органических соединений;
– галогены в твердом и жидком состоянии;
– водород, азот, кислород (связи в молекуле);
– элементы VI группы, V и IV группы (кристаллы алмаза, кремния, германия,  );
);
– химические соединения, подчиняющиеся правилу ( ), если входящие в их состав элементы не находятся в разных концах ряда периодической системы (например,
), если входящие в их состав элементы не находятся в разных концах ряда периодической системы (например,  ).
).
Твердые тела с ковалентными связями могут кристаллизоваться в нескольких структурных модификациях. Это свойство, называемое полиморфизмом, рассматривалось в гл.1.
|
|