Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Парабола

Определение: Параболой называется геометрическое место точек плоскости, равноудаленных от некоторой точки, называемой фокусом параболы и некоторой прямой, называемой директрисой параболы.

Уравнение параболы принятo записывать в следующем виде:

y² = 2px, p> 0 (1)

- каноническое уравнение параболы.

Свойства параболы непосредственно следуют из

свойств уравнения:

1.Абсцисса любой точки параболы неотрицательна.

2.Парабола проходит через начало координат.

3.Парабола симметрична относительно оси абсцисс.

4.При неограниченном возрастании абсциссы x ордината у возрастает по абсолютной величине.

Точка F(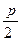; 0) называется фокусом параболы, прямая 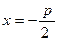- директрисой.

Величина р называется фокальным параметром или просто параметром параболы.

Эллипс

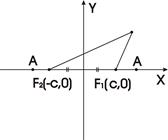Определение. Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек F₁ и F₂ этой плоскости, называемых фокусами эллипса, есть величина постоянная, равная 2 а (а > 0), большая, чем расстояние между фокусами.

Для составления уравнениэллипса выберем прямоугольную декартову систему координат так, чтобы ось ОХ

проходила через фокусы F₁ и F₂, а начало координат — точка О находилась в середине отрезка F₁F₂.

Обозначим F₁F₂ = 2с. Тогда F₁(-с, 0), F₂(c, 0). Пусть М(х, у) – произвольная точка эллипса. Тогда MF₁+ MF₂= 2 а, а > с.

Так как 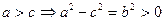, и уравнение принимает вид:

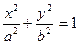. (2)

Пусть координаты точки М₁(х₁, у₁)удовлетворяют уравнению (2).

Обозначим r₁ = F₁M₁, r₂ = F₂M₂ — фокальные радиусы точек М1 М₂. Тогда 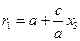, , 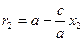значит, r₁+r₂=2 a.

Теперь по свойствам уравнения (2) исследуем геометрические свойства эллипса.

1. Оси ОХ и ОУ являются осями симметрии эллипса. Следовательно, эллипс достаточно исследовать только в первой координатной четверти.

2. Эллипс пересекает координатные оси в точках А₁(- а, 0), А₂(а, 0), В₁(0, b), В₂(0, - b), называемых вершинами эллипса.

3. Эллипс расположен в прямоугольнике, ограниченном прямыми х= 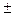а, у = 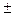b.

4. Из уравнений следует, что при возрастании х от 0 до а в первой координатной четверти, у убывает от b до 0.

По полученным свойствам строим эллипс Отрезок А₁А₂ и его длина 2 а называются большой осью эллипса, а отрезок B₁B₂ и его длина 2 b называются малой осью эллипса. Отрезок ОА₁ с длиной а и отрезок ОВ₁ с длиной b называются соответственно большой и малой полуосями эллипса. Длина отрезка F₁F₂=2 с называется фокусным расстоянием, начало координат— центр эллипса.

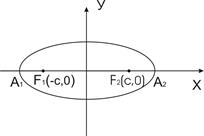Если а = b, то получаем каноническое уравнение окружности

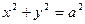
Уравнения х = a cost, у = b sint -

Параметрические уравнения эллипса.