Элементы теории графов

Рассмотрим некоторый общий математический аппарат, который в дальнейшем будет неоднократно использоваться при описании моделей, алгоритмов и компьютерных технологий. Это – теория графов. Формальная конструкция изложена нами в соответствии с широко известной монографией Оре (1980).

5.1. Определения

Предметом первых задач в теории графов были конфигурации, состоящие из точек и соединяющих их линий. В этих рассмотрениях было несущественно, прямые ли это линии или же они являются криволинейными непрерывными дугами, соединяющими две концевые точки, где расположены эти линии, являются ли они длинными или короткими. Существенно только то, что они соединяют две данные точки.

Это приводит к определению графа как абстрактного математического понятия. Рассматривается множество V, состоящее из соединенных некоторым образом точек. Назовем V множеством вершин и элементы v из V — вершинами. Граф

G = (V, E) (5.1)

с множеством вершин V есть некоторое семейство сочетаний или пар вида

Е = (а, b), где a, b из V, (5.2)

указывающее, какие вершины считаются соединенными.

В соответствии с геометрическим представлением графа каждая конкретная пара (5.2) называется ребром графа; вершины а и b называются концевыми точками или концами ребра Е.

Можно использовать и другой подход. Если даны два множества V₁ и V₂, то можно образовать множество всех пар (v₁, v₂), где v₁ из V₁, v₂ из V₂. Это множество пар называется (прямым) произведением и обозначается через V₁× V₂. В нашем случае каждая пара вершин (а, b) есть элемент произведения V× V. Таким образом, можно сказать, что граф G из (5.1) с заданными ребрами (5.2) есть некоторое подмножество произведения V× V.

Это определение графа должно быть дополнено в одном важном отношении. В определении ребра (5.2) можно принимать или не принимать во внимание порядок расположения двух его концов. Если этот порядок не существенен, т. е. если E = (а, b) = (b, а), то говорят, что Е есть неориентированное ребро; если же этот порядок существен, то Е называется ориентированным ребром.

Граф G, не содержащий ориентированных рёбер, называется неориентированным. В дальнейшем будем рассматривать только неориентированные графы.

Говорят, что ребро Е из (5.2) инцидентно вершинам а и b, a также что а и b инцидентны Е.

В приложениях граф G обычно интерпретируется как сеть, в которой вершинами G являются узлы. Два узла a и b соединяются непрерывной кривой (в частности, прямолинейным отрезком) тогда и только тогда, когда в графе G есть пара (5.2). На рисунках узлы будут обычно обозначаться маленькими кружками, а рёбра - дугами.

Вершина, не инцидентная никакому ребру, называется изолированной.

Граф, состоящий только из изолированных вершин, называется нуль - графом и обозначается через 0. Другим важным случаем является (неориентированный) полный граф, ребрами которого являются всевозможные пары (5.2) для двух различных вершин а и b из V. На рис. 5.1 даны схемы полных графов для множеств вершин из четырех и пяти элементов. Сформулированное выше определение графа, вместе с соответствующим изображением, достаточно для многих задач. Однако для некоторых целей желательно понятие графа несколько расширить. Во-первых, можно допускать ребра, у которых концевые вершины совпадают:

L = (a, a) (5.3)

Такое ребро называется петлей. При изображении графа петля бу-

дет представляться замкнутой дугой, возвращающейся в вершину a и не проходящей через другие вершины (рис. 5.2). Во-вторых, можно расширить понятие графа, допуская, чтобы пара вершин соединялась несколькими различными ребрами, у которых обе концевые точки совпадают, как это изображено на рис. 5.3. Такие рёбра назы-

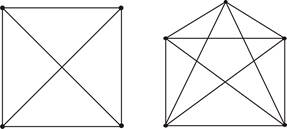
Рис. 5.1. Полные графы для множеств вершин из четырёх и пяти элементов

Рис. 5.2. Петля

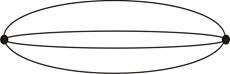
Рис. 5.3. Параллельные рёбра

ваются параллельными. Чтобы проиллюстрировать случай, для которого понятие параллельного ребра оказываются естественными, рассмотрим турнирную таблицу какого-либо командного соревнования, например, четырёхкругового хоккейного чемпионата. Вершинами соответствующего графа являются команды. Пара команд А и В связывается ребром каждый раз, когда они сыграли.

В дальнейшем мы будем рассматривать только графы с конечным числом вершин и рёбер.

5.2. Графы и отношения

Бинарное отношение Rопределяется как соотношение

aRb, (5.4)

которое выполняется для некоторых пар элементов заданного множества V. В соответствии со сказанным выше, бинарное отношение может быть представлено в виде графа с множеством вершин V:

G( R ) = G(V), (5.5)

так что ребро (а, b ) принадлежит G тогда и только тогда, когда в R выполняется соотношение (5.4).

Обратно, любой граф без параллельных рёбер определяет бинарное отношение Rна своем множестве вершин, если положить aRbдля каждого eго ребра. Поэтому можно говорить о взаимно однозначном соответствии между бинарными отношениями на множестве V, с одной стороны, и графами с однократными ребрами на множестве вершин V– с другой.

Остановимся коротко на некоторых связях между бинарными отношениями и графами. Нуль-граф 0 отвечает нулевому отношению

a 0 b,

которое не выполняется ни для какой пары элементов. Полный граф Uотвечает универсальному отношению

aUb,

которое выполняется для любой пары элементов.

Отношение R называется симметричны м, если aRb имеет место в том и только в том случае, когда bRa.

Отношение R называется рефлексивным, если aRa для любого a из V. Соответствующий граф имеет петлю в каждой вершине. Отношение антирефлексивно, если aRa никогда не выполняется, т. е. граф не имеет петель.

Отношение R транзитивно, если из aRb и bRc следует aRc. Для графа это означает, что если G(R) содержит ребра (а, b) и (b, с), то он также содержит и замыкающее ребро (а, с).

Отношения эквивалентности. Отношение R, определенное на множестве V, называется отношением эквивалентности, если оно:

1) рефлексивно,

2) симметрично,

3) транзитивно.

Все элементы из V, эквивалентные данному элементу a, образуют множество R(a), которое называется классом эквивалентности элемента а. Из рефлексивности R следует, что a принадлежит R(a). Если aRb и bRc, то из транзитивности следует aRc, так что R(а) содержит R(b). Поэтому из симметричности отношения мы получаем, что R(а) = R(b) при aRb.

Заметим, что два различных класса эквивалентности R(a) и R(c) не могут иметь какого-либо общего элемента b, так как иначе было бы R(a) = R(c). Таким образом, классы эквивалентности образуют разбиение V, т. е. разложение V на непересекающиеся подмножества. Обратно, по разбиению множества V однозначно порождается отношение эквивалентности R(V).

Если R рефлексивно и симметрично, но не является транзитивным, то оно называется отношением толерантности или «похожести». Например, таковым является отношение R, задаваемое следующим образом: R(a, b) если и только если ½ X(a) – X(b)½ < e, где X – признак, определённый для всех a, bÎ V, e> 0 – вещественное число. Это отношение играет особую роль в анализе данных.

Частичное упорядочение. Отношение a ≤ b, заданное на произвольном множестве V, называется (нестрогим) частичным упорядочением, если оно рефлексивно, транзитивно и

из aRb и bRa следует, что a=b.

Соответствующий граф транзитивен, имеет петли, и любые две вершины в нем соединены не более чем одним ребром.

При строгом частичном упорядочении a< b, которое, также как и нестрогое, обладает свойством транзитивности, соответствующий граф не имеет петель, т.е. ни для какого a из V не выполняется aRa и ни при каких a, b невозможно, чтобы aRb и bRa.

Если для нестрогого или строгого частичного упорядочения для любых a, b из V, таких, что a≠ b, выполняется aRb или bRa, то такое частичное упорядочение называется линейным.

5.3. Матрицы смежности

В разделе 5.1 мы определили ребро Е графа G (см. формулы (5.2), (5.1)) как элемент или точку (a, b) в произведении V× V. Пусть V={a₁, …, a_n}.

Совокупности элементов произведения V× V можно сопоставить квадратную матрицу М=(t_ij)_{n× n}, где каждой паре (a_i, a_j) соответствует пересечение i-ой строки с j-ым столбцом. Положим t_ij = 1, если в G вершины a_i и a_j соединены ребром и t_ij = 0 в противном случае. Таким образом, в случае графа с конечным числом вершин мы получим конечную матрицу смежности вершин M(G), которая полностью описывает G, если граф имеет однократные ребра.

Поскольку в неориентированном графе G (a, b)=(b, a), то можно положить t_ij= t_ji. Таким образом, неориентированным графам соответствуют симметрические матрицы смежности.

5.4. Cвязность

Пусть G – неориентированный граф с конечным числом вершин. Конечным маршрутом в G называется такая конечная последовательность ребер

S = (E₁, …, E_q+1), (5.6)

что каждые два соседних ребра E_j, E_j+1.имеют общую концевую точку. Таким образом, можно написать

E₁=(b₁, b₂), …, E_j=(b_j, b_j+1), …, E_q= (b_q, b_q+1). (5.7)

Отметим, что одно и то же ребро Е может встречаться в маршруте несколько раз.

В дальнейшем рассматриваются только конечные маршруты, поэтому упоминание о конечности маршрута будем опускать; b₁ называется начальной вершиной S, b_q+1 – конечной.

Маршрут назовем нетривиальным, если он содержит хотя бы одно ребро; для систематичности рассуждений в теории графов вводится еще нуль-маршрут, не содержащий ребер. Если a₀, a_n – начальная и конечная вершины маршрута S, то можно написать

S = S(a₀, a_n) (5.8)

и назвать a₀ и а_n концевыми точками, или концами маршрута S. Будем говорить также, что S есть маршрут длины n, соединяющий а₀ и а_n. Если a₀ = а_n, то маршрут называется циклическим. Для двух вершин маршрута a_j, a_k, где j< k, подмаршрут S = S(a_j, a_k) называется участком S.

Маршрут называется цепью, а циклический маршрут – циклом, если каждое его ребро встречается в нем не более одного раза; вершины в цепи могут повторяться и несколько раз. Любой участок цепи есть цепь. Нециклическая цепь называется простой цепью, если в ней никакая вершина не повторяется.

Пусть граф G неориентированный. Две вершины a и b называются связанными, если существует маршрут вида (5.6) с концами a и b. Если S проходит через какую-нибудь вершину c более одного раза, то можно, очевидно, удалить его циклический участок, и при этом остающиеся ребра будут составлять маршрут S', связывающий a и b. Отсюда следует, что связанные маршрутом вершины связаны также простой цепью. Граф называется связным, если любая пара вершин связана.

5.5. Связные компоненты и максимальные клики

Если в произвольном графе G вершина a связана с b, а вершина b связана с вершиной c, то, очевидно, что a связана с вершиной c. Отношение связанности для вершин является отношением эквивалентности.

Подмножество W вершин графа G называется связным в графе G, если для любой пары вершин a_i, a_j из W существует маршрут S(a_i, a_j), состоящий из вершин множества W.

Связное множество является связной компонентой, если оно не является собственным подмножеством никакого другого связного множества.

Важным частным случаем связных множеств является клика – совокупность вершин графа G, в которой любые две вершины инцидентны. Клика называется максимальной, если она не является собственным подмножеством никакой другой клики.

5.6. Расстояния

Пусть G – связный неориентированный граф. Так как любые две вершины а и b связаны, существуют простые цепи S(a, b) с концами а и b. Длины этих простых цепей являются неотрицательными целыми числами. Следовательно, между а и b должны существовать цепи наименьшей длины. Эта наименьшая длина называется расстоянием d(a, b) между a и b. Положим, по определению, d(a, а)=0. Легко видеть, что эта описывающая расстояние функция удовлетворяет аксиомам метрики:

d(a, b) ≥ 0;

d(a, b) = 0 тогда и только тогда, когда а = b;

d(a, b) = d(b, a);

d(a, b) + d(b, c) ≥ d(a, с) для попарно неравных a, b, c. (5.11)