
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Линейные преобразования с простым спектром.
|
|
Во многих случаях оказывается необходимым знать, может ли данное линейное преобразование j иметь в некоторой базе диагональную матрицу. Приведем достаточное условие того, что линейное преобразование может быть задано диагональной матрицей.
Докажем сначала следующие вспомогательные результаты:
Линейное преобразование j тогда и только тогда задается в базе е 1, е 2,..., е n диагональной матрицей, если все векторы. этой базы являются собственными векторами преобразования j.
Действительно, равенство
e ij=li e i
равносильно тому, что в i-й строке матрицы, задающей преобразование j в указанной базе, равны нулю все элементы, стоящие вне главной диагонали, а на главной диагонали (т. е. на i-м месте) стоит число li.
Собственные векторы b 1, b 2, …, b k, линейного преобразования j, относящиеся к различным собственным значениям, составляют линейно независимую систему,
Будем доказывать это утверждение индукцией по k, так как при k =1 оно справедливо - один собственный вектор, будучи отличным от нуля, составляет линейно независимую систему. Пусть
b ij=li b i i = 1, 2, …, k,
и
li ¹ lj при i ¹ j.
Если существует линейная зависимость
a1 b 1+a2 b 2+…+ak b k = 0 (9)
где, например. a1¹ 0, то, применяя к обеим частям равенства (9) преобразование j, получим
a1l1 b 1+a2l2 b 2+…+aklk b k = 0
Вычитая отсюда равенство (9), умноженное на lk, получаем
a1(l1-lk) b 1+a2(l2-lk) b 2+…+ak-1(lk-1-lk) b k-1 = 0
что дает нетривиальную линейную зависимость между векторами b 1, b 2, …, b k-1, так как a1(l1-lk)¹ 0.
Говорят, что линейное преобразование j действительного линейного пространства Vn имеет простой спектр, если все его характеристические корни действительны и различны. Преобразование. j имеет, следовательно, n различных собственных значений, а поэтому, по доказанной теореме, в пространстве Vn существует база, составленная из собственных векторов этого преобразования. Таким образом, всякое линейное преобразование с простыми спектром может быть задано диагональной матрицей.
Переходя от линейного преобразования к матрицам, его задающим, мы получаем следующий результат:
Всякая матрица, все характеристические корни которой действительны и различны, подобна диагональной матрице или, как говорят, такая матрица приводится к диагональному виду.
34)
Евкли́ дово простра́ нство (также Эвкли́ дово простра́ нство) — в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность 3.
В современном понимании, в более общем смысле, может обозначать один из сходных и тесно связанных объектов, определённых ниже. Обычно n -мерное евклидово пространство обозначается  , хотя часто используется не вполне приемлемое обозначение
, хотя часто используется не вполне приемлемое обозначение  .
.
1. Конечномерное гильбертово пространство, то есть конечномерное вещественное векторное пространство  с введённым на нём (положительно определенным) скалярным произведением, порождающим норму:
с введённым на нём (положительно определенным) скалярным произведением, порождающим норму:
 ,
,
в простейшем случае (евклидова норма):

где  (в евклидовом пространстве всегда можно выбрать базис, в котором верен именно этот простейший вариант).
(в евклидовом пространстве всегда можно выбрать базис, в котором верен именно этот простейший вариант).
2. Метрическое пространство, соответствующее пространству описанному выше. То есть  с метрикой, введённой по формуле:
с метрикой, введённой по формуле:
 ,
,
где  и
и 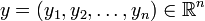 .
.
Вектор. Ортонормированный базис. Если векторы e 1, e 2, e 3 попарно перпендикулярны и длина каждого из них равна единице, то базис называется ортонормированным, а координаты x 1, x 2, x 3 - прямоугольными. Базисные векторы ортонормированного базиса будем обозначать i, j, k.
Будем предполагать, что в пространстве R 3 выбрана правая система декартовых прямоугольных координат {0, i, j, k }.
Вектор. Векторное произведение. Векторным произведением вектора а на вектор b называется вектор c, который определяется следующими тремя условиями:
1. Длина вектора c численно равна площади параллелограмма, построенного на векторах a и b, т. е. ê c ê = ê a ê ê b ê sin (a ^ b).
2. Вектор c перпендикулярен к каждому из векторов a и b.
3. Векторы a, b и c, взятые в указанном порядке, образуют правую тройку.
Для векторного произведения c вводится обозначение c = [ ab ] или
c = a ´ b.
Если векторы a и b коллинеарны, то sin(a^b) = 0 и [ ab ] = 0, в частности, [ aa ] = 0. Векторные произведения ортов: [ ij ] = k, [ jk ] = i, [ ki ] = j.
Если векторы a и b заданы в базисе i, j, k координатами a (a 1, a 2, a 3), b (b 1, b 2, b 3), то
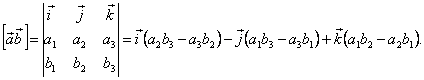
(неопределённость  ). Пусть функции f (х) и g (х): 1. непрерывны на полуинтервале (a, b]; 2.
). Пусть функции f (х) и g (х): 1. непрерывны на полуинтервале (a, b]; 2. 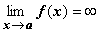 ,
,  ; 3. существуют производные f '(х) и g'(х) на интервале (a, b), причём g'(х) ¹ 0; 4. существует (конечный или бесконечный)
; 3. существуют производные f '(х) и g'(х) на интервале (a, b), причём g'(х) ¹ 0; 4. существует (конечный или бесконечный)  . Тогда существует
. Тогда существует  , и
, и  .
.
Теорема остаётся справедливой и для случаев  . В целом теоремы Лопиталя - это мощное средство для раскрытия неопределённостей всех видов.
. В целом теоремы Лопиталя - это мощное средство для раскрытия неопределённостей всех видов.
Соответствия. Функции и отображения. Операции. Перестановки, размещения и сочетания. Упорядоченные и неупорядоченные разбиения множества. Инверсии и обратные перестановки. Перманенты и их применения. Алгоритмы генерации комбинаторных объектов.
35)
|
|