
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Матрица линейного преобразования
|
|
В примере 19.4 было показано, что преобразование  -мерного пространства, заключающееся в умножении координатных столбцов векторов на фиксированную матрицу, является линейным преобразованием. В этом разделе мы покажем, что все линейные преобразования конечномерного пространства устроены таким же образом. Пусть
-мерного пространства, заключающееся в умножении координатных столбцов векторов на фиксированную матрицу, является линейным преобразованием. В этом разделе мы покажем, что все линейные преобразования конечномерного пространства устроены таким же образом. Пусть 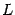 --
--  -мерное линейное пространство, в котором задан базис
-мерное линейное пространство, в котором задан базис 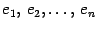 ,
, 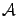 -- линейное преобразование. Возьмем произвольный вектор
-- линейное преобразование. Возьмем произвольный вектор  . Пусть
. Пусть 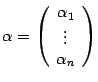 -- его координатный столбец. Координатный столбец вектора
-- его координатный столбец. Координатный столбец вектора 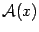 обозначим
обозначим 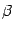 . Запишем разложение вектора
. Запишем разложение вектора  по базису пространства
по базису пространства 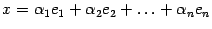 . Для образа этого вектора получим
. Для образа этого вектора получим 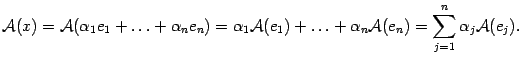 (19.2) Векторы
(19.2) Векторы 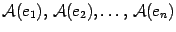 имеют какие-то координатные столбцы, обозначим их
имеют какие-то координатные столбцы, обозначим их 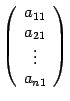 ,
, 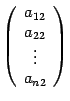 ,...,
,..., 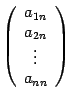 соответственно. В этой записи первый индекс показывает номер координаты, а второй индекс -- номер вектора. Соответственно,
соответственно. В этой записи первый индекс показывает номер координаты, а второй индекс -- номер вектора. Соответственно, 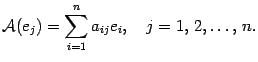 Подставим это выражение в равенство (19.2) и, используя предложение 14.3, изменим порядок суммирования
Подставим это выражение в равенство (19.2) и, используя предложение 14.3, изменим порядок суммирования  Это равенство означает, что
Это равенство означает, что 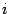 -той координатой вектора
-той координатой вектора 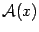 служит
служит 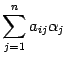 . Составим матрицу
. Составим матрицу  из координатных столбцов векторов
из координатных столбцов векторов  ,...,
,..., 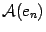
 Вычислим произведение матрицы
Вычислим произведение матрицы  на столбец
на столбец 
 Мы видим, что
Мы видим, что 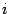 -ый элемент столбца совпадает с
-ый элемент столбца совпадает с 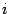 -ой координатой вектора
-ой координатой вектора 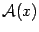 . Поэтому
. Поэтому  (19.3) Это означает, что в выбранном базисе действие любого линейного преобразования сводится к умножению матрицы на координатный столбец вектора. Матрица
(19.3) Это означает, что в выбранном базисе действие любого линейного преобразования сводится к умножению матрицы на координатный столбец вектора. Матрица  называется матрицей линейного преобразования
называется матрицей линейного преобразования 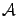 . Еще раз напомним, как она составлена: первый столбец является координатным столбцом образа первого базисного вектора, второй столбец -- координатным столбцом образа второго базисного вектора и т.д. Пример 19. 5 Найдем матрицу линейного преобразования
. Еще раз напомним, как она составлена: первый столбец является координатным столбцом образа первого базисного вектора, второй столбец -- координатным столбцом образа второго базисного вектора и т.д. Пример 19. 5 Найдем матрицу линейного преобразования 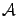 из примера 19.1. Выберем какой-нибудь базис
из примера 19.1. Выберем какой-нибудь базис 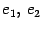 . Тогда
. Тогда  Следовательно, первый столбец матрицы
Следовательно, первый столбец матрицы  имеет вид
имеет вид 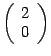 . Аналогично
. Аналогично 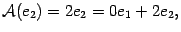 Второй столбец матрицы
Второй столбец матрицы  имеет вид
имеет вид 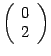 . В итоге
. В итоге  Пример 19. 6 Найдем матрицу линейного преобразования
Пример 19. 6 Найдем матрицу линейного преобразования 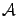 из примера 19.2. Угол
из примера 19.2. Угол 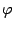 возьмем равным
возьмем равным  . В качестве базиса возьмем привычный ортонормированный базис i, j. Из рисунка 19.7 видно, что вектор
. В качестве базиса возьмем привычный ортонормированный базис i, j. Из рисунка 19.7 видно, что вектор  имеет координаты
имеет координаты 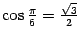 и
и 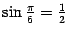 .
.  Рис. 19. 7.Координаты образов базисных векторов при преобразовании поворота Поэтому координатный столбец образа первого базисного вектора имеет вид
Рис. 19. 7.Координаты образов базисных векторов при преобразовании поворота Поэтому координатный столбец образа первого базисного вектора имеет вид 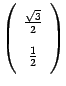 . Координаты образа второго базисного вектора равны
. Координаты образа второго базисного вектора равны 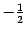 и
и  , его координатный столбец имеет вид
, его координатный столбец имеет вид 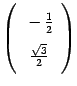 . В итоге получаем, что в базисе i, j матрица поворота на угол
. В итоге получаем, что в базисе i, j матрица поворота на угол  имеет вид
имеет вид 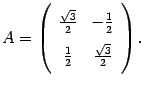
31)
Характеристический многочлен матрицы — это многочлен, определяющий её собственные значения.
|
|