
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Что такое матрицы инциденций и как они составляются?
|
|
Ответ: Схемы замещения современных сложных электрических систем содержат сотни узлов и ветвей. Количество уравнений состояния для таких систем соответственно настолько велико, что для их решения необходимо использовать ЭВМ. Для этого требуется иметь формализованный подход к составлению уравнений, который был бы одинаков для схем любой сложности и конфигурации. Такой подход может быть разработан на основе аналитического представления конфигурации схемы замещений с помощью элементов теории графов и алгебры матриц. Схема замещения электрической системы, используемая для расчетов установившихся режимов, представляет собой электрическую цепь, содержащую пассивные и активные элементы и к ней применимы такие понятия, как ветвь, узел и контур. Конфигурацию схемы замещения электрической системы можно отобразить в виде графа. Графпредставляет собой множество вершин (узлов) и ребер (ветвей), соединяющих некоторые (или все) пары вершин. Любая часть графа называется подграфом. Совокупность ребер, соединяющих две произвольные вершины, образуют подграф, определяемый как путь графа. Если начальная и конечная вершины пути графа совпадают, то этот путь графа является замкнутым и образует контур. Ветви, связанные с узлом нейтрали (ветви источников питания и нагрузок), называют поперечными; остальные ветви – продольными. Схема замещения, имеющая хотя бы один контур, называется замкнутой; при отсутствии контуров – разомкнутой. Если в графе можно выбрать путь, который соединяет его любые две вершины, то этот граф является связанным; если нельзя – несвязанным. Если ребра графа имеют фиксированные направления, то этот граф называется направленным. Каждое ребро направленного графа имеет начальную и конечную вершины; его направление принимается от первой вершины ко второй. Схема замещения электрической системы обычно является связанным графом, ребрами которого служат ветви, а вершинами – узлы. Ветви образуют цепочки (пути графа), которые могут быть замкнутыми. Все величины, характеризующие состояние ветвей (токи, ЭДС, падения напряжения), имеют определенное направление (без чего не может быть рассчитан режим данной схемы). В связи с этим целесообразно каждой ветви схемы придать определенное (произвольно выбранное) направление. Для обобщенного аналитического представления направленного графа служат матрица соединений ветвей в узлах М (первая матрица инциденций) и матрица соединений ветвей в независимые контуры N (вторая матрица инциденций). Первая матрица инциденций – это прямоугольная матрица (n × m), число строк которой равно числу вершин графа n, а число столбцов – числу ребер m: 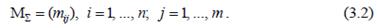 Номера строк i соответствуют номерам вершин, а номера столбцов j - номерам ребер. Элементы матрицы
Номера строк i соответствуют номерам вершин, а номера столбцов j - номерам ребер. Элементы матрицы 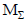 могут принимать одно из трех значений:
могут принимать одно из трех значений: 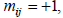 если узел i является начальной вершиной ветви j (ток ветви выходит из i -го узла);
если узел i является начальной вершиной ветви j (ток ветви выходит из i -го узла); 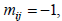 если узел i является конечной вершиной ветви j (ток ветви
если узел i является конечной вершиной ветви j (ток ветви
входит в j -й узел); 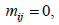 если узел i не является вершиной ветви j (нет связи между
если узел i не является вершиной ветви j (нет связи между
i -м узлом и j -й ветвью). Каждая строка матрицы 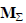 показывает, какими вершинами соответствующие ветви присоединяются к данному узлу схемы; каждый столбец – какие узлы являются начальной и конечной вершинами данной ветви. Очевидно, что в каждом столбце матрицы
показывает, какими вершинами соответствующие ветви присоединяются к данному узлу схемы; каждый столбец – какие узлы являются начальной и конечной вершинами данной ветви. Очевидно, что в каждом столбце матрицы 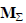 может быть только одна положительная и одна отрицательная единицы; остальными
может быть только одна положительная и одна отрицательная единицы; остальными
элементами являются нули. Сумма всех строк этой матрицы (по столбцам) должна давать нулевую (строчную) матрицу. Вторая матрица инциденций– это прямоугольная матрица 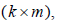 число строк которой равно числу независимых контуров графа k, а число столбцов – числу ребер m:
число строк которой равно числу независимых контуров графа k, а число столбцов – числу ребер m: 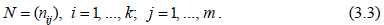 Номера строк i соответствуют номерам независимых контуров, а номера столбцов j – номерам ветвей. Элементы матрицы N могут принимать одно из трех значений:
Номера строк i соответствуют номерам независимых контуров, а номера столбцов j – номерам ветвей. Элементы матрицы N могут принимать одно из трех значений: 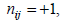 если ветвь j входит в i -й контур и их направления совпадают;
если ветвь j входит в i -й контур и их направления совпадают;  если ветвь j входит в i -й контур, но направления противоположны;
если ветвь j входит в i -й контур, но направления противоположны; 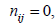 если ветвь j не входит в i -й контур. Каждая строка матрицы N показывает, какие ветви входят в состав соответствующего независимого контура и какое направление имеют относительно направления контура. Каждый столбец матрицы показывает, в состав каких независимых контуров входит данная ветвь и совпадает ли ее направление с направлениями этих контуров. Ни рис. 3.1 приведены направленный граф и соответствующие ему матрицы инциденций.
если ветвь j не входит в i -й контур. Каждая строка матрицы N показывает, какие ветви входят в состав соответствующего независимого контура и какое направление имеют относительно направления контура. Каждый столбец матрицы показывает, в состав каких независимых контуров входит данная ветвь и совпадает ли ее направление с направлениями этих контуров. Ни рис. 3.1 приведены направленный граф и соответствующие ему матрицы инциденций. 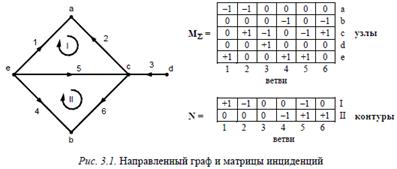 Матрицы
Матрицы 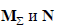 дают возможность записать уравнения состояния электрической цепи в матричной форме. Конкретный вид этих уравнений определяется формами уравнений состояния, положенных в основу математического описания установившегося режима, и обобщенными параметрами системы. Из уравнений состояния наиболее широко при- меняются узловые уравнения, которые характеризуются как простотой формирования, так и большими возможностями эффективной организации процесса их решения. Контурные уравнения формируются несколько сложнее, однако и они имеют определенную рациональную область применения.
дают возможность записать уравнения состояния электрической цепи в матричной форме. Конкретный вид этих уравнений определяется формами уравнений состояния, положенных в основу математического описания установившегося режима, и обобщенными параметрами системы. Из уравнений состояния наиболее широко при- меняются узловые уравнения, которые характеризуются как простотой формирования, так и большими возможностями эффективной организации процесса их решения. Контурные уравнения формируются несколько сложнее, однако и они имеют определенную рациональную область применения.
|
|