Характеристики и анализ свойств систем массового обслуживания

1. Характеристики СМО общего вида G/G/1

Наиболее общим случаем одноканальных систем массового обслуживания являются СМО типа G/G/1, в которую поступает произвольный поток заявок общего вида с функцией распределения интервалов между заявками A(τ). Длительность обслуживания заявок в приборе распределена по произвольному закону B(τ).

Расчет таких систем требует задания конкретных законов распределений, что не позволяет получить аналитическое решение в общем виде. Аналитическое решение возможно только для некоторых частных распределений, связанных, например, с экспоненциальным распределением. Для большинства законов распределений интервалов между поступающими в систему заявками и длительностей их обслуживания в приборе невозможно получить точное решение в аналитической форме.

В то же время, на практике при исследовании реальных систем редко бывают известны законы распределений указанных величин. Обычно при описании процессов поступления заявок в систему и их обслуживания в приборе ограничиваются несколькими моментами соответствующих распределений, чаще всего – двумя первыми моментами, задаваемыми в виде математического ожидания и среднеквадратического отклонения или коэффициента вариации искомой случайной величины. Однако при этом оказывается невозможным получение точного результата. Это обусловлено тем, что в случае произвольного (отличного от простейшего) потока заявок, поступающих в систему, характеристики функционирования СМО, в частности среднее время ожидания, зависят не только от двух первых моментов, но и от моментов более высокого порядка – третьего, четвёртого и т.д. Причём эта зависимость тем меньше, чем выше порядок числового момента. Таким образом, все результаты, полученные в аналитической форме при задании интервалов между поступающими в систему заявками и длительностей их обслуживания в приборе двумя первыми моментами – средними значениями a =1/ λ и b =1/ µ и коэффициентами вариации ν _a и ν _b, представляют собой приближённые зависимости.

Как показал анализ многочисленных опубликованных результатов, одним из наиболее удачных приближений для расчета среднего времени ожидания в СМО G/G/1 является следующая формула [17]:

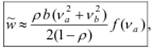(4.6)

где ρ = λ b < 1 – загрузка системы; λ, ν _a – интенсивность потока заявок и коэффициент вариации интервалов между поступающими в систему заявками; b, ν _b – среднее значение и коэффициент вариации длительности обслуживания заявок; f (ν _a) – корректирующая функция, рассчитываемая в зависимости от значения коэффициента вариации ν _a:

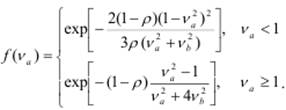
При решении многих практических задач выходящий поток заявок из одной СМО является входящим потоком в другую СМО. В этом случае для расчёта характеристик функционирования второй СМО необходимо знать характер входящего потока, наиболее полно описываемый законом распределения интервалов между последовательными заявками. В то же время, для проведения оценочных расчётов во многих случаях достаточнознание первых двух моментов этих интервалов: математического ожидания и коэффициента вариации.

Очевидно, что в СМО с накопителем неограниченной ёмкости, работающей без перегрузок, интенсивность выходящего потока заявок равна интенсивности входящего потока, то есть математические ожидания интервалов между последовательными заявками на выходе и входе СМО совпадают.

Можно показать, что для экспоненциальной СМО М/М/1 коэффициент вариации выходящего потока равен единице.

В общем случае для СМО G/G/1 коэффициент вариации выходящего потока заявок может быть рассчитан по следующей приближённой формуле [17]:

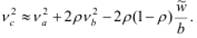(4.7)