
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Центр масс сплошных тел
|
|
В предыдущем параграфе мы ввели понятие центра масс системы материальных точек. В том случае, когда имеется сплошное тело, задача нахождения координат центра масс решается следующим образом. Распределение массы можно охарактеризовать физической величиной, называемой плотностью тела r. Если тело однородно, то его свойства одинаковы во всех точках и плотность тела равна
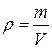 , (2.3.1)
, (2.3.1)
где 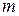 — масса тела, а
— масса тела, а 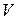 — его объем. Следовательно, плотность вещества
— его объем. Следовательно, плотность вещества 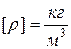 — это масса единицы объема. Если тело неоднородно, то его плотность в разных точках различна. В этом случае она определяется как предел отношения массы
— это масса единицы объема. Если тело неоднородно, то его плотность в разных точках различна. В этом случае она определяется как предел отношения массы 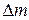 заключенной в некотором малом объеме
заключенной в некотором малом объеме 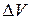 . Обратим внимание, что малый объем
. Обратим внимание, что малый объем 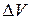 не стягивается в точку. Он должен быть с одной стороны малым по сравнению с объемом тела
не стягивается в точку. Он должен быть с одной стороны малым по сравнению с объемом тела 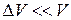 , а с другой стороны достаточно большим, чтобы в него входило достаточно большое количество атомов. Поэтому масса i -ого элемента равна
, а с другой стороны достаточно большим, чтобы в него входило достаточно большое количество атомов. Поэтому масса i -ого элемента равна 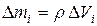 .
.
Масса сплошного тела равна сумме масс этих малых элементов,
а в пределе определяется интегралом по объему тела:
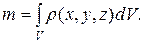 (2.3.2)
(2.3.2)
Если в формулах для координат центра масс (3.2.3) перейти от суммирования к интегрированию, то координата 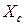 центра масс определяется следующим выражением:
центра масс определяется следующим выражением:
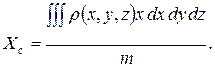 (2.3.3)
(2.3.3)
Аналогичные соотношения будут иметь место и для других координат центра масс.
Достаточно очевидно, что вычисление координат центра масс сплошного тела представляет собой достаточно сложную математическую задачу. В то же время знание положения центра масс имеет очень важное значение во многих задачах механики. В некоторых случаях положение центра масс легко определить из соображений симметрии или путем достаточно простых вычислений. Приведем сведения о положении центра масс некоторых тел.
Если тело имеет симметрию и однородно, то центр масс такого тела лежит на оси симметрии.
1. Тонкая однородная прямоугольная пластинка. Из соображений симметрии ясно, что ее центр масс совпадает с геометрическим центром, т.е. лежит в точке пересечения диагоналей.
2. Однородный прямоугольный стержень (параллелепипед). Из тех же соображений ясно, что его центр масс находится в геометрическом
центре.
3. Треугольник. Центр масс лежит в точке пересечения его медиан.
4. Параллелограмм. Центр масс лежит на пересечении диагоналей.
5. Шар. Центр масс находится в центре шара.
6. Однородный диск (цилиндр). Центр масс лежит в геометрическом центре.
Очень часто используют понятие центра тяжести. Центр тяжести — это точка, к которой приложена равнодействующая всех сил тяжести данного тела. В общем случае центр тяжести и центр масс могут не совпадать.
Рассмотрим ряд примеров вычисления координат центра масс. Часто удается тело сложной формы представить в виде суммы тел, положение центров масс которых известно.
Пример. Два шара массами m 1 = 3 кг и m 2 = 5 кг скреплены стержнем, масса которого m 3 = 2 кг. Определить положение общего центра масс, если R 1=5 см, R 2=7 см, а длина стержня равна 30 см (рис. 2.1).
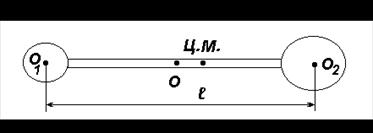
Рис. 2.1. К определению центра масс распределенной системы
Прежде всего, необходимо выбрать систему координат. Этот выбор произволен и мы поместим начало координат в центре первого шара.
В этой системе координаты центров масс всех тел известны. Поэтому
имеем:
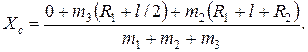
Выполнив численный расчет, получим: Xc = 0, 25 м, но обязательно надо добавить: от центра первого шара.
Если мы начало координат поместим в точку, где находится центр масс стержня, то имеем:
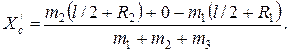
Нетрудно показать, что центр масс находится на расстоянии 0, 05 м вправо от середины стержня.
Пример. Две стороны проволочной рамки в форме равностороннего треугольника сделаны из алюминиевой проволоки, а третья — из медной. Проволоки имеют одинаковые сечения, а сторона треугольника равна l = 1м. Плотности алюминия и меди соответственно равны 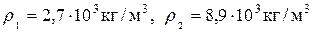 (рис. 2.2.). Найти положение центра масс системы.
(рис. 2.2.). Найти положение центра масс системы.
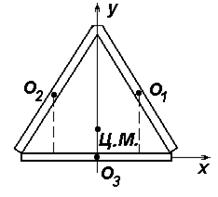
Рис. 2.2. К определению центра масс представленной системы
Положение центров масс элементов рамки известны — это середины их отрезков. Но их положение следует определить в выбранной системе координат. Поместим начало координат в середину медного отрезка
(точка О 3).
Тогда имеем:
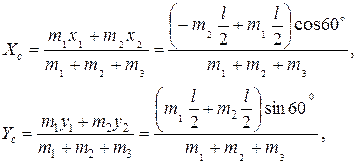
где 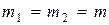 — массы алюминиевых стержней, а
— массы алюминиевых стержней, а 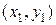 и
и 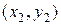 — координаты их центров масс, соответственно.
— координаты их центров масс, соответственно.
Поскольку длины и сечения сторон треугольника одинаковы,
то имеем:
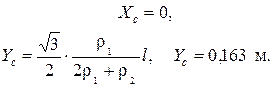
Данный пример показывает, что центр масс может лежать вне тела, Кроме того, поскольку стороны рамки изготовлены из разных материалов, т. е. тело неоднородно, то центр масс не лежит на пересечении медиан.
Рассмотренные примеры показывают некоторые приемы определения координат центра масс сплошных тел. Естественно, что эти приемы не являются универсальными, но часто могут облегчить решение задачи.
Отметим важность указания положения центра масс при описании движения тела. Роль положения центра масс продемонстрируем на следующих простых примерах.
|
|