
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Характеристики моделей кривых роста
|
|
Комплекс аналитических методов выравнивания сводится к выбору конкретных кривых роста и определению их параметров. Под кривой роста понимают функцию, аппроксимирующую заданный динамический ряд.
К первому классу относятся кривые, которые используются для описания процессов с монотонным характером развития и отсутствием пределов роста.
Ко второму классу относятся кривые, имеющие предел роста в исследуемом периоде. Такие кривые называют кривыми насыщения.
Если кривые насыщения имеют точки перегиба, то они относятся к кривым третьего класса. Их называют S - образными кривыми.
Среди кривых роста первого типа выделяют класс полиномов:
уt = а0 + а1t + а2t2 + а3t3 +...
Параметр а0 является начальным уровнем ряда при t = 0,
а1 - линейный прирост,
а2 — ускорение роста,
а3 — изменение ускорения роста.
В экономических исследованиях в большинстве случаях применяются полиномы не выше третьего порядка.
Полином первой степени
уt = a0 + a1t
на графике изображается в виде прямой и используется для описания процессов, развивающихся равномерно во времени.
Полином второй степени
уt = а0 + а1t + а2t2
на графике изображается в виде параболы и применяется в тех случаях, когда процесс развивается равноускоренно. Если a2 > О, то ветви параболы направлены вверх, в случае а2 < 0 — вниз.
Полином третьей степени
уt = а0 + а1t + а2t2+ а3t3
У полинома третьей степени знак прироста ординат может изменяться один или два раза.
Оценки параметров полиномов определяются методом наименьших квадратов. Так, нормальное уравнение для определения коэффициентов прямой имеет вид
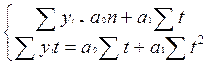
Систему нормальных уравнений можно упростить и уменьшить абсолютные значения величин, если перенести начала координат в середину ряда динамики. Если до переноса начало координат t равно 1, 2, 3..., то после переноса получим:
• для четного числа членов t=..., -5. -3, -1, 1, 3, 5...,
• для нечетного числа членов t: =..., -3, -2, -1, 0, 1, 2, 3...
|
|