
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Типовые динамические звенья. Разновидности, классификация.
|
|
Классификация звеньев производится именно по виду дифференциального уравнения. Одним и тем же уравнением могут описываться весьма разнообразные устройства (механические, гидравлические, электрические и т. д.). Обозначим входную величину звена через х1, а выходную через х2. Возмущение, действующее на звено, в соответствии с изложенным выше обозначим f(T). Статическая характеристика любого звена может быть изображена прямой линией, так как пока будут рассматриваться линейные или, точнее, линеаризованные системы.В звеньях позиционного, или статического, типа линейной зависимостью х2 = kх1 связаны выходная и входная величины в установившемся режиме. Коэффициент пропорциональности k между выходной и входной величинами представляет собой коэффициент передачи звена.
В звеньях интегрирующего типа линейной зависимостью dх2 /dt = kх1 связаны производная выходной величины и входная величина в установившемся режиме. В этом случае для установившегося режима будет справедливым равенство х2 = k∫ х1dt,. Коэффициент пропорциональности k в этом случае также является коэффициентом передачи звена. Если входная и выходная величины звена имеют одинаковую размерность, то коэффициенту передачи соответствует размерность [с-1].
В звеньях дифференцирующего типа линейной зависимостью х2 = kdх1/dt связаны в установившемся режиме выходная величина и производная входной. Коэффициент пропорциональности k является коэффициентом передачи звена. Если входная и выходная величины имеют одинаковую размерность, то коэффициенту передачи в этом случае соответствует размерность [с].
 32. Инерционное звено первого порядка. Звено описывается дифференциальным уравнением
32. Инерционное звено первого порядка. Звено описывается дифференциальным уравнением 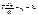 Передаточная функция звена
Передаточная функция звена 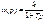
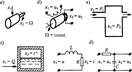
Примеры апериодических звеньев первого порядка изображены на рис. 4.10.
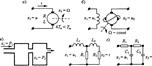
В качестве первого примера (рис. 4.10, а) рассматривается двигатель любого типа (электрический, гидравлический, пневматический и т. д.), механические характеристики которого (зависимость вращающего момента от скорости) могут быть представлены в виде параллельных прямых (рис. 4.11). Входной величиной х\ здесь является управляющее воздействие в двигателе, например подводимое напряжение в электрическом двигателе, расход жидкости в гидравлическом двигателе и т. п
Постоянная времени характеризует «инерционность» или «инерционное запаздывание» апериодического звена. Выходное значение х^-Нх^ъ апериодическом звене устанавливается только спустя некоторое время (? п) после подачи входного воздействия.
Амплитудно-фазовая характеристика для положительных частот имеет вид полуокружности с диаметром, равным коэффициенту передачи k. Величина постоянной времени звена определяет распределение отметок частоты вдоль кривой.
Из амплитудной характеристики видно, что колебания малых частот (ω < 1/Т) «пропускаются» данным звеном с отношением амплитуд выходной и входной величин, близким к статическому коэффициенту передачи звена k. Колебания больших частот (ω > 1/Т) проходят с сильным ослаблением амплитуды, т. е. «плохо Пропускаются» или практически совсем «не пропускаются» звеном. Чем меньше постоянная времени T, т. е. чем меньше инерционность звена, тем более вытянута амплитудная характеристика A(ω) вдоль оси частот, или, как говорят, тем шире полоса пропускания частот у данного звена.
Логарифмические частотные характеристики строится по выражению 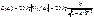
33. Безынерционное звено. Это звено не только в статике, но и в динамике описывается алгебраическим уравнением
х2 = kх1. Передаточная функция звена равна постоянной величине:
W(р) = W(jω) = k.
Примером такого звена являются механический редуктор (без учета явления скручивания и люфта), безынерционной (широкополосный) усилитель, делитель напряжения и т. п. Многие датчики сигналов, как, например, потенциометрические датчики, индукционные датчики, вращающиеся трансформаторы и т. п., также могут рассматриваться как безынерционные звенья.
Переходная функция такого звена представляет собой ступенчатую функцию, т. е. при х1{t) = 1(t), х2(t) = h(t) = k • 1(t).
А. ф. х. вырождается в точку, расположенную на вещественной оси на расстоянии Н от начала координат. Модуль частотной передаточной функции А(ω) = k постоянен на всех частотах, а фазовые сдвиги равны нулю (\|/ = 0).
Безынерционное звено является некоторой идеализацией реальных звеньев. В действительности ни одно звено не в состоянии равномерно пропускать все частоты от 0 до °°. Обычно к такому виду звена сводится одно из реальных звеньев, рассматриваемых ниже, например апериодическое или колебательное, если можно пренебречь влиянием динамических (переходных) процессов в этом звене.
34. Апериодическое звено второго порядка. Дифференциальное уравнение звена имеет вид
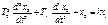
При этом корни характеристического уравнения 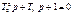 должны быть вещественными, что будет выполняться при условии T1 ≥ 2T2. В операторной записи равнение (4.25) приобретает вид
должны быть вещественными, что будет выполняться при условии T1 ≥ 2T2. В операторной записи равнение (4.25) приобретает вид 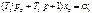
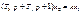
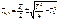
Передаточная функция звена 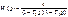
Апериодическое звено второго порядка эквивалентно двум апериодическим звеним первого порядка, включенным последовательно друг за другом, с общим коэффициентом передачи k и постоянными времени Tз и Т4.
Примеры апериодических звеньев второго порядка приведены на рис.
|
|