
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Элементы теории вероятности.
|
|
Случайные события - это всякое явление, которое либо может произойти, либо нет. Случайные события некоторых событий субъективны, т. е. обусловлены недостаточностью знаний, или технической возможностью для точного предсказания. Но чаще случайный характер объективен, а сама постановка вопроса о самом предсказании лишена физического смысла.
Для случайных событий необходимо пользоваться необходимым понятием соответствующим математическим аппаратом, этим занимается теория вероятности.
Случайная величина (событие) - это событие, которое нельзя заранее точно предсказать.
Вероятность события - это количественная характеристика, определяемая возможность события.
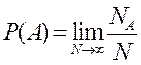 , где
, где
Рисунок 5.2
P(A) - вероятность события А;
N - количество совершённых событий;
NA - количество совершившихся событий А.
Сложение вероятностей взаимно исключающих событий.
Событие взамоисключающее, если появление одного события исключает появление другого.
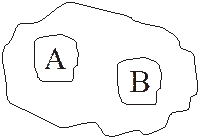
Рисунок 5.3
Вероятность того, что произойдёт событие сразу нескольких событий, равна произведению вероятности этих событий.
P(AB)=P(A) * P(B)
Сложение в общем случае.
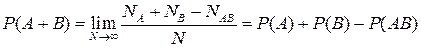
Р(АВ) вероятность, что произошло событие А и В.
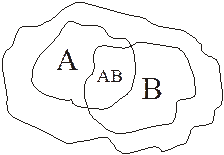
Рисунок 5.4
Вероятность достоверного события
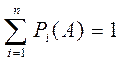
Среднее ожидание случайной величины за N испытаний:

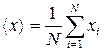
Среди значений xi могут быть одинаковые величины, поэтому правую часть необходимо перегрупировать, для того чтобы в нее входили только разные xi
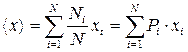
Ni число одинаковых членов, имеющих значения xi
Pi вероятность события i;
< x> математическое ожидание случайной величины с учётом вероятности.
Для непрерывных значений:
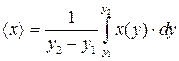
|
|