Частина 1

Для студентів 2-го курсу спеціальності 0908

Тема роботи: Визначення робочої смуги частот підсилювачів за шириною спектра сигналів

Мета роботи: Набуття навичок практичного застосування основних положень теорії спектрів періодичних процесів і дослідження впливу обмеження ширини смуги пропускання на спотворення форми сигналів на виході підсилювача.

Завдання на роботу:

1. Для заданого процесу за його комплексним спектром знайти:

1.1. Комплексний ряд Фур’є процесу

1.2. Математичний та фізичний спектри амплітуд та фаз процесу

1.3. Дійсний ряд Фур’є процесу

2. Побудувати графіки математичного та фізичного спектрів амплітуд та фаз процесу

3. Зробити 6 рисунків, на яких в одному масштабі побудувати:

3.1. Графік заданого процесу та його постійну складову

3.2. Графік процесу, його постійну складову та першу гармоніку

3.3. Графік процесу, його постійну складову та суму першої і другої гармонік

3.4. Графік процесу, його постійну складову та суму перших трьох гармонік

3.5. Графік процесу, його постійну складову та суму перших чотирьох гармонік

3.6. Графік процесу, його постійну складову та суму перших п’яти гармонік

4. Робота повинна задовольняти вимогам, викладеним в загальних методичних вказівках.

Вихідні дані:

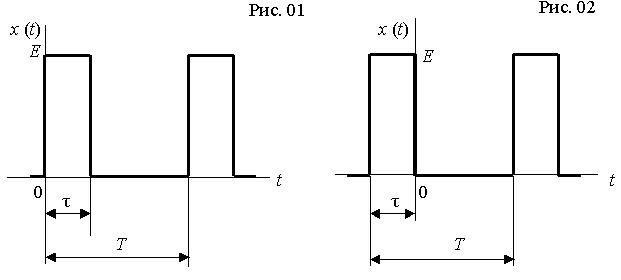
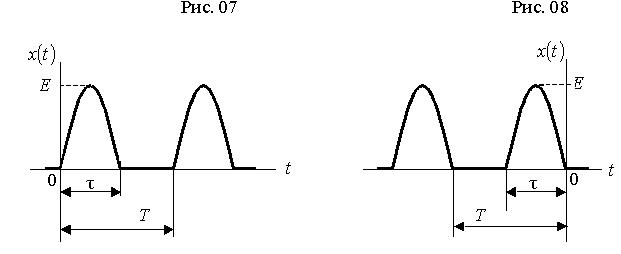
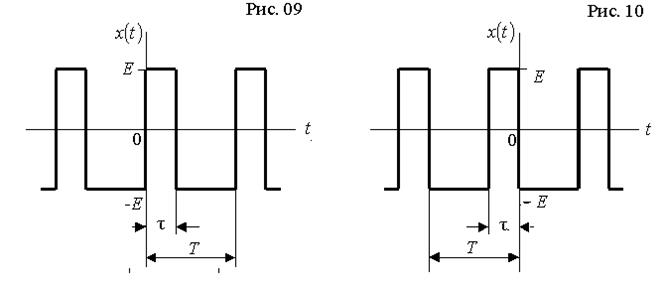
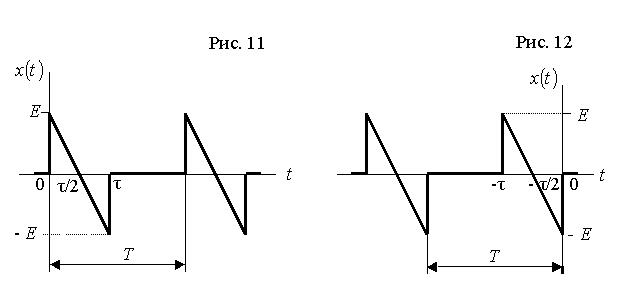
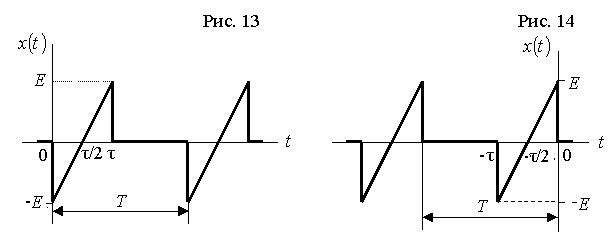
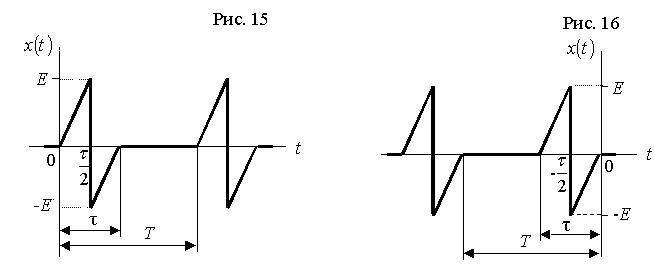
Вихідними даними до виконання роботи є тризначний номер варіанта завдання, який викладач призначає індивідуально кожному студенту. Перші дві цифри номеру варіанта означають двозначний номер рисунку, на якому наведено графік заданого процесу та математичний вираз його комплексного спектра. Ці рисунки наведені після таблиці 1. За третьою цифрою номеру варіанту визначається значення параметра періодичного процесу – шпаруватості q: q = Т / τ,

де T і τ – період та тривалість імпульсів заданого процесу 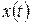. Величина параметра q визначається за допомогою таблиці 1.

Таблиця 1.

Приклади отримання вихідних даних:

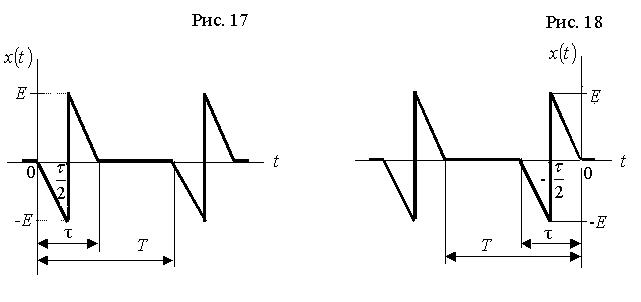
для виконання роботи за варіантом 143 необхідно взяти процес, графік якого наведено на рис. 14, зі шпаруватістю q =4;

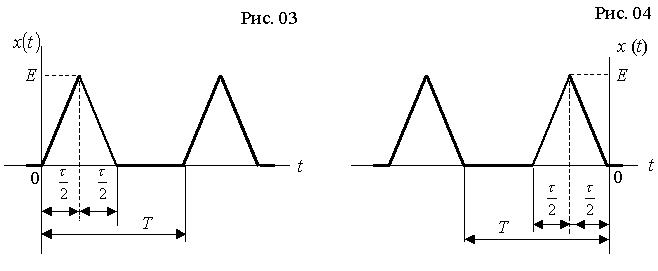
для виконання роботи за варіантом 033 необхідно взяти процес, графік якого наведено на рис. 03, зі шпаруватістю q =4.

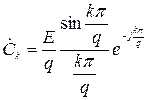
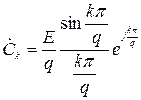
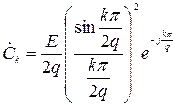
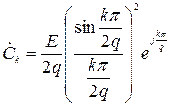
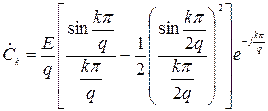
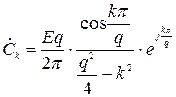
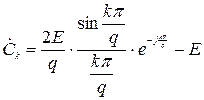
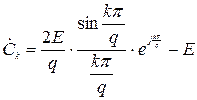
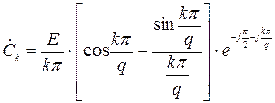
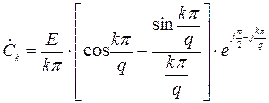
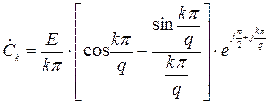
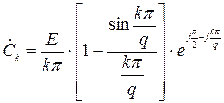
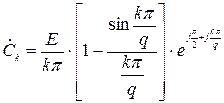
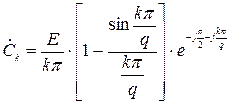
Методичні вказівки до виконання роботи:

до п. 1.1 завдання. Для всіх періодичних процесів 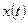комплексний ряд Фур’є має однаковий вираз:

,

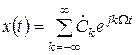де Ω = 2 π / T – основна частота процесу з періодом T. Вираз для комплексних коефіцієнтів 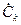наведено під графіком заданого процесу.

до п. 1.2 завдання. Для отримання математичних спектрів амплітуд та фаз періодичного процесу необхідно комплексний спектр цього процесу, який є сукупністю комплексних коефіцієнтів 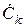, представити у показовій формі:

,

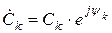де 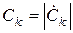- модулі комплексних коефіцієнтів 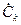, сукупність яких утворює математичний спектр амплітуд, а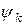 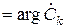- аргументи комплексних коефіцієнтів 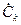, сукупність яких утворює математичний спектр фаз періодичного процесу.

Комплексні спектри заданих в роботі процесів представлені у вигляді:

.

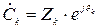Це не є представленням комплексного спектра у показовій формі, в загальному випадку множник 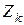на одміну від суттєво позитивного множника може приймати для різних k як позитивні, так і негативні значення. Якщо 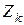не є строго позитивним за будь-яких k, то для отримання математичного спектра амплітуд необхідно прийняти:

.

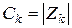Тоді комплексний спектр процесу отримає вигляд:

Якщо множник –1 представити в експоненціальній формі:

,

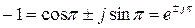то остаточно комплексний спектр процесу у показовій формі прийме вигляд:

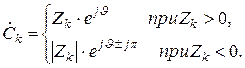
Звідси знаходиться математичний спектр фаз процесу:

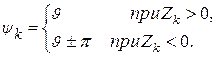
Знак перед π можна вибирати як позитивним, так і негативним, але здебільшого його приймають протилежним до знаку .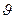

Фізичні спектри амплітуд та фаз отримуються з математичних спектрів процесу. Фізичний спектр амплітуд 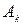отримується з математичного спектра шляхом відкидання з від’ємними номерами та подвоєння амплітуд з позитивними k, окрім постійної складової:

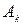= 2 , , ,

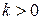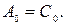Фізичний спектр фаз отримується з математичного спектра шляхом простого відкидання з від’ємними номерами.

до п. 1.3 завдання. Для всіх періодичних процесів 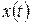дійсний ряд Фур’є має однаковий вираз:

,

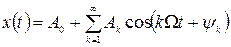де сукупності амплітуд 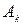і початкових фаз утворюють фізичні спектри амплітуд та фаз.

до п. 2 завдання. Для досягнення більшої наочності графіки математичного та фізичного спектрів повинні мати однакові масштаби по осям координат. При цьому слід враховувати, що математичні спектри існують як на позитивних, так і на негативних частотах, а фізичні спектри – лише на позитивних частотах. При побудові математичних спектрів слід мати на увазі, що математичні спектри амплітуд є парними, а математичні спектри фаз – непарними функціями частоти. Для побудови графіків спектрів результати розрахунків значень , , 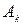і доцільно звести в таблицю (див. табл. 2).

до п. 3 завдання. Мета виконання п. 3 завдання полягає в порівнянні заданого періодичного процесу з його скінченим рядом Фур’є за різного числа N врахованих гармонічних складових процесу.

Основою для побудови скінчених рядів Фур’є є дійсний ряд Фур’є, отриманий при виконанні п. 2. Скінчений ряд Фур’є зручно представити у вигляді:

.

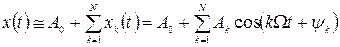З цього виразу видно, що всі гармонічні складові 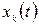коливаються не навколо нуля, а навколо постійної складової 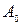і будуються однаковим чином з одиничного гармонічного процесу 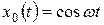, для якого A ₀ = 0, A= 1, ψ ₀ =0, а ω =2 π /Т, де Т – періодпроцесу.

Графік процесу 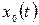будується по точках. При цьому чим ближчими вибираються точки, тим точнішою, але й складнішою, є сама побудова. Для навчальних цілей достатньо приймати густину точок рівною 8 точок / період. Тоді інтервал між точками по осі t дорівнюватиме 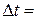Т/ 8, а математична модель процесу 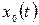прийме вигляд:

,

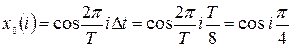де i – номер точки. В таких точках процес 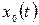прийматиме лише значення або ±1, або ± 1/ 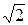= ± 0, 707, або 0.

Приклад побудови процесу 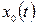ілюструється на рис. 19, 20, 21. На рис. 19 відображено систему координат, де вісь абсцис розмічена в долях періоду гармоніки Т, а вісь ординат – в долях одиниці. На рис. 20 ілюструється техніка побудови процесу 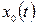. Точки, де 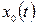= 0 і суміжні по обидві сторони від них,

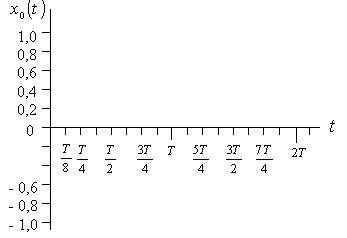
Рис. 19

де 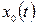=±0, 707, з’єднуються відрізками прямої. Через точки, де 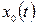приймає екстремальні значення ±1, проводяться невеличкі дуги, дотичні до яких є паралельними до осі t. Після цього не важко з’єднати дуги з відрізками прямої (рис. 21).

Рис. 20

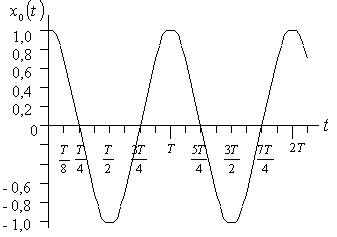
Рис. 21

Для побудови гармонічних складових 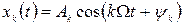процесу 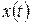потрібно скласти таблицю 2 необхідних для побудов даних. Стовпчики таблиці мають такий зміст:

Таблиця 2.

k	Сk	Ak	ψ k	Tk	ε k	τ k
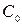
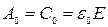
			-	-	ε 0	-
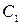
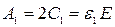
			ψ 1	Т	ε 1	τ 1 =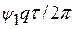
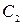
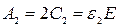
			ψ 2	Т/2	ε 2	τ 2 =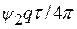
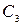
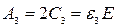
			ψ 3	Т/3	ε 3	τ 3 =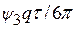
			ψ 4	Т/4	ε 4	τ 4 =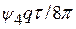
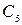
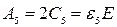
			ψ 5	Τ /5	ε 5	τ 5 =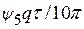

- k – номер гармоніки;

- С_k – математичний спектр амплітуд;

- A_k – фізичний спектр амплітуд, амплітуда k -ї гармонічної складової заданого процесу ;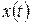

- ψ _k - спектр фаз, початкова фаза k -ї гармонічної складової заданого процесу ;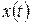

- T_k – період k -ї гармонічної складової заданого процесу 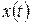, T_k = ¥ при k= 0 і T_k = Т/k при k > 0;

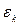- - коефіцієнт амплітуди гармонічних складових заданого процесу : ;

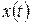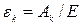- τ _k – затримка (зсув) k -ї гармонічної складової заданого процесу .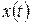

Значення параметрів гармонічних складових заданого процесу 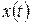для заповнення стовпчиків С_k, A_k, ψ _k розраховані в п. 2. Значення параметрів T_k, ε _k розраховуються за наведеними формулами. Необхідність стовпчика τ _k зумовлена тим, що гармоніки 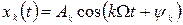треба розташовувати на осі часу разом з заданим процесом 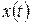. Однак на осі часу неможливо відкласти початкову фазу ψ _k. Для розташування 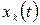на осі t необхідно в дужках виразу для 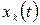мати змінну t без коефіцієнта, тобто представити: 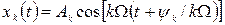. Тоді величина τ _k = 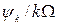матиме розмірність часу і її можна відкладати на осі часу. Затримку τ _k зручно виразити через тривалість імпульсу τ заданого процесу 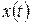: τ _k = = .

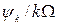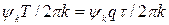При побудові графіків заданого процесу 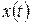та його гармонік необхідно вибирати масштаб по осях координат. В разі використання паперу формату А4 прийнятні наочність та точність побудов будуть досягнутими, якщо вибрати амплітуду процесу Е® 50…100 мм, період процесу Т® 120 мм.

Для прикладу розглянемо процес, представлений на рис. 01, зі шпаруватістю q = 2. За результатами розрахунків, отриманими при виконанні п.2, складаємо за зразком таблиці 2 таблицю 3. Подальша послідовність дій визначається пп. 3.1...3.6 завдання.

Таблиця 3.

k	Сk	Ak	ψ k	Tk	ε k	τ k
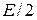
		E/ 2	-	¥	0, 5	-
	0, 318 E	0, 636 E	- π /2	Т	0, 636	-τ /2
			-	-		-
	0, 106 E	0, 212 E	-π /2	Т/3	0, 212	-τ /6