
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретические основы. В общем случае функция напряжений для вязкоупругого материала имеет интегральный вид
|
|
В общем случае функция напряжений для вязкоупругого материала имеет интегральный вид. В контексте теории малых деформаций определяющее уравнение для изотропного вязкоупругого материала может быть записано в следующей форме:
 , (4.60)
, (4.60)
где σ – напряжения по Коши;
e – девиаторная часть деформаций;
δ – объемная часть деформаций;
I – единичный тензор;
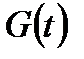 – ядро релаксации для модуля сдвига;
– ядро релаксации для модуля сдвига;
K(t) – ядро релаксации для объемного модуля;
t – текущее время;
τ – прошлое время.
Ядра релаксации раскладываются в ряды Прони:
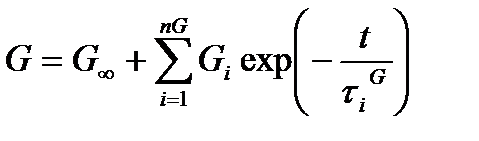 , (4.61)
, (4.61)
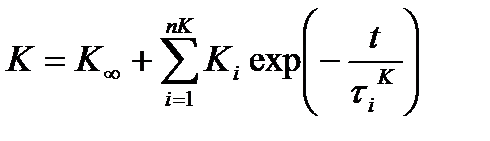 , (4.62)
, (4.62)
где i – номер члена ряда Прони;
Gi и Ki – члены ряда Прони для модулей сдвига и объемного сжатия соответственно;
G∞ и K∞ – финальные модули сдвига и объемного сжатия соответственно;
nG и nK – число членов ряда Прони для модулей сдвига и объемного сжатия соответственно;
τ iG и τ iК – время релаксации для соответствующего члена ряда Прони.
Введем начальный (мгновенный) модуль сдвига 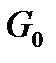 и объемный модуль начальный (мгновенный)
и объемный модуль начальный (мгновенный) 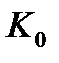 , равные:
, равные:
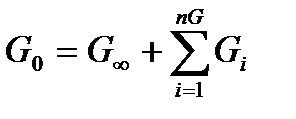 , (4.63)
, (4.63)
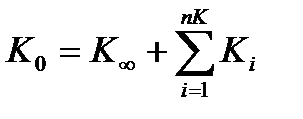 , (4.64)
, (4.64)
и относительные модули, равные:
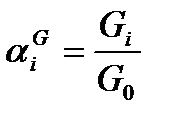 , (4.65)
, (4.65)
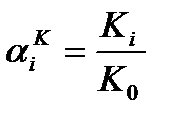 . (4.66)
. (4.66)
Очевидно, что ядра релаксации могут быть представлены в следующем виде:
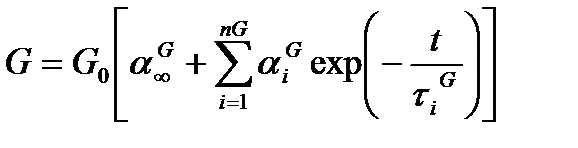 ,
, 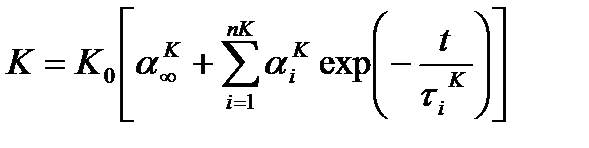 . (4.67)
. (4.67)
Интегральная функция (4.60) соответствует упругому поведению материала при очень быстрой и очень долгой нагрузке. Мгновенные модули 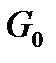 и
и 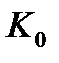 отвечают за упругое поведение при быстротечном воздействии, а финальные модули G∞ и K∞ – при очень долгом нагружении (см рисунок 4.10). А в соответствии с (4.67) происходит релаксация девиаторной и объемной составляющих напряжений.
отвечают за упругое поведение при быстротечном воздействии, а финальные модули G∞ и K∞ – при очень долгом нагружении (см рисунок 4.10). А в соответствии с (4.67) происходит релаксация девиаторной и объемной составляющих напряжений.
Количество членов ряда Прони для модулей сдвига и объемного сжатия nG и nK может быть различным, также как и времена релаксации τ iG и τ iК могут не совпадать.
В практике численного моделирования иногда используют упрощенную вязкоупругую модель поведения материала:
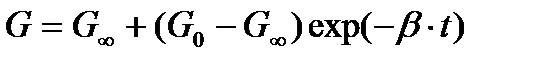 , (4.68)
, (4.68)
где β – коэффициент релаксации.
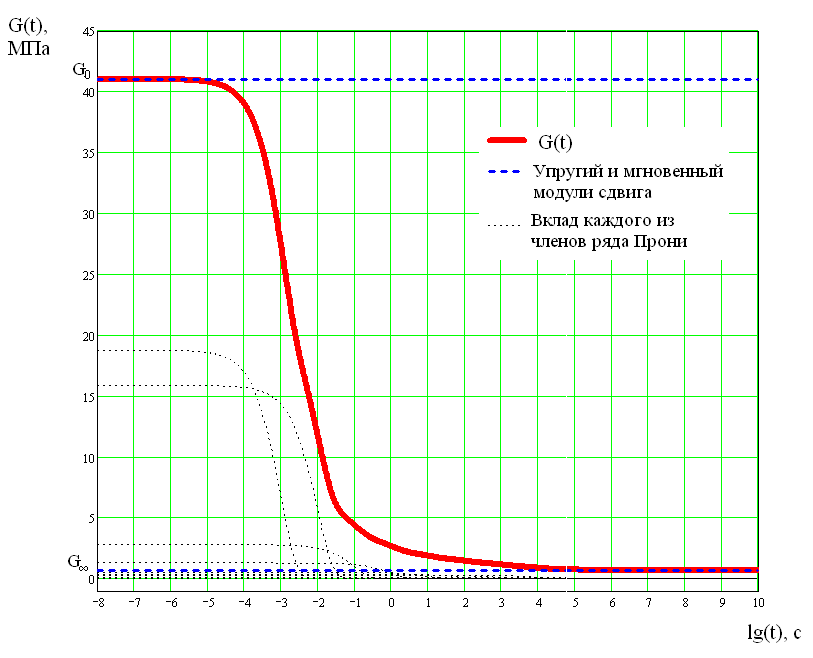
Рисунок 4.10 - Ядро релаксации модуля сдвига G (типичное для твердого ракетного топлива)
|
|