
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Краткое теоретическое введение. Алгоритм уточнения корня методом половинного деления
|
|
Алгоритм уточнения корня методом половинного деления
Сущность метода. Пусть каким-либо методом найден отрезок изоляции корня [а; b] уравнения F(х) = 0, где F(х) - непрерывна на участке [a; b], (а)*F(b) < 0. В дальнейшем требуется сузить этот отрезок так, чтобы его длина стала не больше заранее заданной точности вычисления корня e, то есть чтобы |b - a| £ e.
Этот процесс сужения интервала, содержащего изолированный корень уравнения F(х) = 0, называется уточнением корня.
В этом алгоритме отрезок изоляции корня [а; b] точкой с = 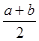 делят пополам и вычисляют значение F(c). Если F(c) = 0, то с - значение искомого корня уравнения, и задача решена. Если F(c) ¹ 0, то искомый корень уравнения содержится в одном из двух отрезков [a; c] или [c; b], на концах которого функция F
делят пополам и вычисляют значение F(c). Если F(c) = 0, то с - значение искомого корня уравнения, и задача решена. Если F(c) ¹ 0, то искомый корень уравнения содержится в одном из двух отрезков [a; c] или [c; b], на концах которого функция F  принимает значения разных знаков. Обозначим этот отрезок через [a1, b1], его длина b1-a1 =
принимает значения разных знаков. Обозначим этот отрезок через [a1, b1], его длина b1-a1 = 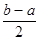 . С отрезком [a1, b1] поступают точно так, как и с отрезком [a, b]. Этот процесс последовательного деления отрезка пополам продолжают до тех пор, пока не произойдет одно из двух:
. С отрезком [a1, b1] поступают точно так, как и с отрезком [a, b]. Этот процесс последовательного деления отрезка пополам продолжают до тех пор, пока не произойдет одно из двух:
§ либо найдется такая точка cn =  , в которой F(cn) = 0 (что маловероятно!), и задача решена;
, в которой F(cn) = 0 (что маловероятно!), и задача решена;
§ либо такой точки не найдется, но при некотором n придем к отрезку [an, bn] длины bn - an = 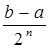 £ e, содержащему в себе искомый корень.
£ e, содержащему в себе искомый корень.
Тогда числа an и bn являются приближенными значениями искомого корня с требуемой точностью e соответственно с недостатком и с избытком. Однако лучше за приближенное значение искомого корня взять число сn = 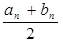 , погрешность которого не превышает
, погрешность которого не превышает 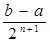 .
.
Алгоритм уточнения корня методом хорд
Сущность метода. Пусть отрезок изоляции [a; b] корня х уравнения F(х) = 0 найден, причем для определенности пусть F(a) < 0, F(b) > 0 и F'(х) > 0. График функции y = F(х) проходит через точки A(a; F(a)) и B(b; F(b)) (рис. 1). Составим уравнение хорды АВ как прямой, проходящей через точки А и В:
y = kx + l;
F(a) = ka + l;
F(b) = kb + l;
k = 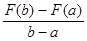 ; l = F(a) - a
; l = F(a) - a 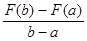
y= 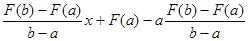
y - F(a) = 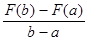 (x - a).
(x - a).
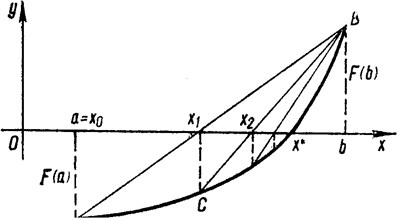
Рис. 1 – Графическое представление метода хорд
далее находим абсциссу x1 точки пересечения хорды АВ с осью Ох, уравнение которой y = 0:
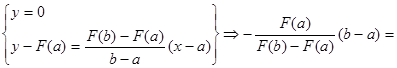
= x1 - a Þ x1 = a -  .
.
Число x1 примем за первое приближение корня х*. Далее, применяя этот же прием к отрезку изоляции [x1; b], на концах которого функция F(x) принимает противоположные знаки, получим второе приближение корня x2:
x2 = x1 - 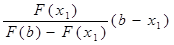
Этот процесс можно продолжать неограниченно. Описанный процесс называется методом хорд. В результате получим последовательность вложенных отрезков[a; b] É [x1; b] É [x2; b] É... É [xn; b] É ... с неподвижным концом b. Последовательные приближения xn (n = 1, 2,...) к точному значению корня х* вычисляются по формуле
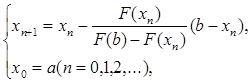 (1)
(1)
называемой формулой метода хорд, и образуют монотонно возрастающую последовательность a = x0 < x1 < x2 <... < xn < xn+1 <... < b, ограниченную сверху числом b. По теореме Вейерштрасса эта последовательность имеет предел
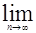 xn =
xn = 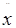 *.
*.
Поскольку F(х) непрерывна на [а; b], то 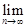 F(xn) = F(
F(xn) = F(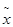 *).
*).
Переходя теперь к пределу в равенстве (1), получаем
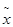 * =
* = 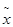 * -
* - 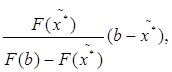
откуда, так как b - 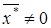 , следует, что F(
, следует, что F(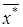 ) = 0. Но в связи с тем, что уравнение F(x) = 0 на отрезке [а; b]имеет единственный корень х *, то х * = х *.
) = 0. Но в связи с тем, что уравнение F(x) = 0 на отрезке [а; b]имеет единственный корень х *, то х * = х *.
Поскольку полученная последовательность (х„) сходится к корню уравнения х *, то любой ее член можно рассматривать в качестве приближенного значения корня. Практически последовательные приближения вычисляют до тех пор, пока не получат приближенное значение корня с требуемой точностью.
Алгоритм уточнения корня методом касательных
Сущность метода. Пусть [а; b] — отрезок изоляции корня х * уравнения F(х) = 0. И пусть для определенности F(a)< 0, F(b)> 0, F‘(x) > 0 и F ” (x) > 0, xÎ [а; b], то есть производные сохраняют постоянный знак (рис.2). Идея метода касательных, предложенного Ньютоном, сводится к замене небольшой дуги кривой у = F(х) касательной к кривой, проведенной в некоторой точке интервала [а; b]. Выберем, например, x0 = b, так как F(x0) ´ F¢ ¢ (x0)> 0, и в точке В(x0, F(х0)) проведем касательную к кривой у = F(х). Ее уравнение: y - F(x0) = F¢ (x0)(x - x0). '
Найдем теперь точку пересечения x1 касательной с осью Ох (у = 0):
0 - F(x0) = F¢ (x0)(x1 - x0) Þ x1 = x0 - 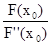
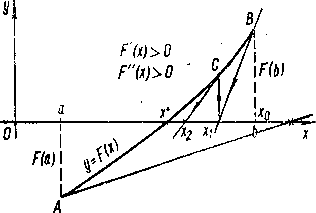
Рис. 2 – Графическое представление метода касательных
Эту точку x1 принимаем за первое приближение искомого корня х *. Через точку С(x1; F(x1)) снова проведем касательную y - F(x1) = F‘(x1)(x - x1), абсциссу точки пересечения которой с осью Ох примем за второе приближение х2 корня х *.
Имеем: 0 - F(x1) = F‘(x1)(x2 - x1) Þ x2 = x1 - 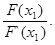
Продолжая этот процесс далее, получим рекуррентную формулу,
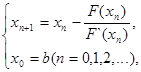
называемую формулой метода касательных.
Заметим, что если в рассматриваемом случае (F’(x) > О, F”(x) > О, F(b) > 0, F(а) < 0) касательную провести в точке А, то есть положить x0 = а, то точка пересечения ее с осью абсцисс может оказаться вне отрезка изоляции корня [a; b]. Это значит, что метод касательных неприменим, если в качестве начальной точки x0 выбрать такую, в которой F(x0) ´ F”(x0) < 0.
Как и в методе хорд, можно доказать (предлагаем читателю сделать это самостоятельно), что полученная числовая последовательность
x0> x1> x2>...> xn> xn+1>...> a
сходится к корню уравнения х *.
Для оценки погрешности приближения xn можно воспользоваться, как и в методе хорд, формулой
½ x* - xn½ £ ½ xn - xn-1½ £ e.
Анализируя возможные расположения кривой у = F(х)на отрезке изоляции, где последовательные приближения по методу касательных обозначены 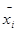 (i = 0, 1, 2...), получаем правило для использования метода касательных: в качестве начального приближения x0 выбирается тот конец отрезка изоляции (x0 = а или x0 = b), в котором выполняется условие
(i = 0, 1, 2...), получаем правило для использования метода касательных: в качестве начального приближения x0 выбирается тот конец отрезка изоляции (x0 = а или x0 = b), в котором выполняется условие
F(x0) F¢ ¢ (x0) > 0
Метод последовательных приближений (итераций)
Сущность метода. Для нахождения действительных корней уравнения F(x) = 0, где F(x) - непрерывная функция на [a; b], его заменяют равносильным уравнением
х = j(х) (2)
Это можно сделать всегда, притом не одним способом. Например, уравнение х3 - 9х + 3 = 0 можно представить так:
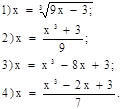
Пусть известен отрезок изоляции корня [a; b], тогда за начальное приближение искомого корня уравнения (2) берут: 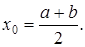 Подставляя значение х0 в правую часть уравнения (2), получают первое приближение х1 = j(х0). В качестве второго приближения берут х2 = j(х1). Продолжая этот процесс дальше, получают числовую последовательность (хn), определенную с помощью рекуррентной формулы:
Подставляя значение х0 в правую часть уравнения (2), получают первое приближение х1 = j(х0). В качестве второго приближения берут х2 = j(х1). Продолжая этот процесс дальше, получают числовую последовательность (хn), определенную с помощью рекуррентной формулы:
xn+1 = j(xn), (n = 0, 1, 2,...) (3)
Полученная последовательность х0, х1,..., xn, xn+1,... называется итерационной последовательностью, способ построения ее называется методом последовательных приближений или методом итераций численного решения уравнения.
При пользовании методом итераций необходимо выяснить основной вопрос: сходится ли полученная последовательность (хn) к решению х* уравнения (2) при возрастании n? Если последовательность (хn) сходится, то есть существует предел х* = 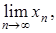 то, переходя к пределу в равенстве (3) и, предполагая, что функция j(х) непрерывна, получаем:
то, переходя к пределу в равенстве (3) и, предполагая, что функция j(х) непрерывна, получаем:
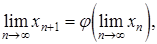 или x* = j(x*).
или x* = j(x*).
Следовательно, в этом случае х = х* является корнем уравнения х = j(х), а значит, и уравнения F(x) = 0.
Если же последовательность (хn) окажется расходящейся, то есть не существует конечного предела построенной последовательности приближений (хn), то это означает, что процесс итераций построен неудачно, и его надо заменить другим.
Следовательно, метод последовательных приближений применим при выполнении условия: ½ j‘(x)½ £ M1 < 1
для всех х, принадлежащих отрезку изоляции корня уравнения (2), В этом случае процесс итераций сходится, и тем быстрее, чем меньше М1; если же ½ j‘(x)½ > 1, то итерационный процесс расходится. Для конкретной оценки величины m1, определяющей скорость сходимости, проще всего пользоваться формулой: М1 = max½ j‘(x)½, где max берется по отрезкуизоляции корня [а: b].
Задание на работу
В соответствии с вариантом задания (см. Приложение), полученным у преподавателя (вид функции в виде f(x)=0), необходимо:
1. Изучить численные основные методы определения корней уравнений (половинного деления, касательных, хорд, хорд и касательных).
2. Получить интервал локализации корня уравнения, используя:
а) аналитический метод;
б) метод табуляции.
3. Составить блок-схему и программу, которая позволит:
а) уточнить корень методом половинного деления (для всех номеров);
б) уточнить корень методом касательных (для нечетных номеров);
в) уточнить корень методом хорд (для четных номеров);
г) уточнить корень методом итераций.
После определения корней необходимо подставить значение корня для проверки правильности решения.
Результаты вывести в виде, удобном для восприятия.
Содержание отчета: титульный лист, тема и цель работы, № варианта задания и собственно задание, описание типов функциональных рядов по методам вычислений, определение типа заданного ряда, математическая постановка задачи и определение области допустимых значений (ОДЗ), блок-схема алгоритма, текст программы и результаты её работы. Работу программы студент обязан показать на ПЭВМ.
Контрольные вопросы.
1. Обоснуйте необходимость приближенного решения алгебраических и трансцендентных уравнений.
2. Аналитический метод отделения корней уравнения.
3. Отделения корней уравнения методом перебора.
4. Метод половинного деления: преимущества и недостатки.
5. Метод Ньютона (касательных). Выбор начального приближения для выполнения условия сходимости процесса.
6. Использование метода хорд для уточнения корней уравнения.
7. Смысл метода итераций. Преимущества и недостатки по отношению к другим методам.
|
|