
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теорема Банаха.
|
|
Пусть 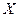 - банахово пространство. Рассмотрим уравнение
- банахово пространство. Рассмотрим уравнение
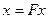 , (1)
, (1)
где 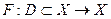 - (в общем случае) нелинейный оператор. Если
- (в общем случае) нелинейный оператор. Если 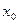
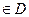 является решением уравнения (1), т.е. справедливо равенство
является решением уравнения (1), т.е. справедливо равенство 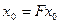 , то
, то 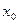 называется неподвижной точкой (элементом) оператора
называется неподвижной точкой (элементом) оператора 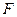 .
.
Утверждения о существовании неподвижных точек составляют специальный раздел функционального анализа, который имеет многочисленные приложения, в том числе, для доказательства существования решения краевых задач для систем обыкновенных дифференциальных уравнений.
Пусть 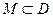 . Говорят, что оператор
. Говорят, что оператор 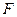 на множестве
на множестве 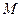 удовлетворяет условию Липшица с постоянной
удовлетворяет условию Липшица с постоянной 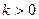 , если для любых
, если для любых 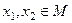 выполняется неравенство
выполняется неравенство
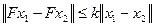 .
.
Очевидно, что такой оператор является непрерывным. Если 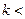 1, то оператор
1, то оператор 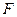 осуществляет сжимающееся отображение множества
осуществляет сжимающееся отображение множества 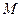 (является оператором сжатия).
(является оператором сжатия).
Теорема (Банах). Пусть 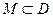 непустое замкнутое множество и оператор
непустое замкнутое множество и оператор 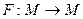 удовлетворяет условию Липшица с постоянной
удовлетворяет условию Липшица с постоянной 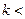 1. Тогда существует единственная неподвижная точка оператора
1. Тогда существует единственная неподвижная точка оператора 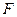 , принадлежащая
, принадлежащая 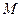 .
.
Доказательство. Докажем, что неподвижную точку можно найти как предел последовательности приближения. Произвольно зафиксируем 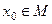 и построим последовательность
и построим последовательность 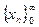
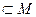 следующим образом: положим
следующим образом: положим 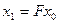 ,
, 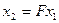 ,
, 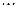
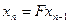 .
.
Сначала докажем, что 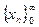 является фундаментальной последовательностью. Пусть
является фундаментальной последовательностью. Пусть 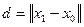 . Тогда
. Тогда
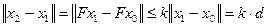 ,
,
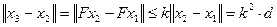
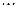
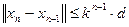
Учитывая, что 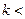 1, оценим (
1, оценим (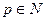 )
)
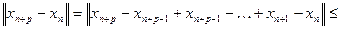
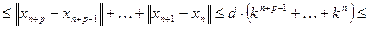
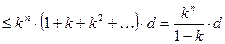 .
.
Следовательно, 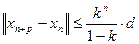 . Из этого неравенства и
. Из этого неравенства и 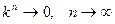 следует, что
следует, что 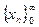 - фундаментальная последовательность. В силу замкнутости
- фундаментальная последовательность. В силу замкнутости 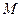 последовательность
последовательность 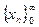 имеет предел
имеет предел 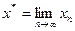 ,
,  .
.
Рассмотрим равенство 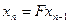 и перейдем в нем к пределу при
и перейдем в нем к пределу при 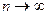 . Учитывая непрерывность (из условия Липшица) оператора
. Учитывая непрерывность (из условия Липшица) оператора 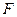 , получим
, получим
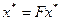 .
.
Это и означает, что 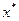 - неподвижная точка оператора
- неподвижная точка оператора 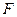 .
.
Докажем единственность неподвижной точки. Доказательство проведем «от противного». Пусть существует две неподвижные точки 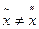 . Тогда
. Тогда
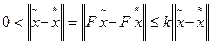 .
.
Отсюда получим, что 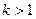 , что противоречит условию теоремы. Полученное противоречие, доказывает, что неподвижная точка единственна. Теорема доказана.
, что противоречит условию теоремы. Полученное противоречие, доказывает, что неподвижная точка единственна. Теорема доказана.
Подчеркнем, что построенные в доказательстве приближения стремятся к единственной неподвижной точке независимо от выбора «начального приближения» 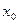 . Тот или иной выбор
. Тот или иной выбор 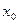 влияет только на «скорость» сходимости в качестве коэффициента. При этом сама сходимость определяется постоянной Липшица: чем меньше константа, тем быстрее сходится приближение с порядком сходимости
влияет только на «скорость» сходимости в качестве коэффициента. При этом сама сходимость определяется постоянной Липшица: чем меньше константа, тем быстрее сходится приближение с порядком сходимости 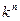 . Отметим также, что в условиях теоремы Банаха выполнение условия
. Отметим также, что в условиях теоремы Банаха выполнение условия 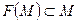 существенно. Теорема Банаха позволяет доказать не только существование неподвижной точки, но устанавливает факт её единственности.
существенно. Теорема Банаха позволяет доказать не только существование неподвижной точки, но устанавливает факт её единственности.
В качестве примера применения теоремы Банаха рассмотрим задачу Коши для обыкновенного дифференциального уравнения.
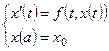 (1)
(1)
где 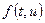 - непрерывная функция двух переменных.
- непрерывная функция двух переменных.
Искомое решение 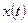 предполагается непрерывно дифференцируемой функцией, определенной на
предполагается непрерывно дифференцируемой функцией, определенной на 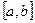 .
.
Рассмотрим интегральное уравнение
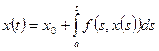 (2)
(2)
в пространстве 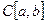 . Если существует решение уравнения (2), то оно является и решением задачи Коши (1). Действительно, при выполнении (2) функция
. Если существует решение уравнения (2), то оно является и решением задачи Коши (1). Действительно, при выполнении (2) функция 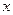
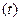 непрерывна и непрерывно дифференцируема. Продифференцируем (2) и получим, что решение уравнения (2) удовлетворяет и дифференциальному уравнению задачи (1). Кроме того, при
непрерывна и непрерывно дифференцируема. Продифференцируем (2) и получим, что решение уравнения (2) удовлетворяет и дифференциальному уравнению задачи (1). Кроме того, при 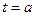 выполняется и начальное условие.
выполняется и начальное условие.
Представим уравнение (2) в виде операторного уравнения
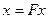 ,
,
где 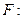
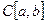
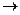
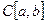 , полагая
, полагая
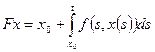 .
.
Для доказательства существования единственности решения задачи Коши проверим, что оператор 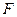 удовлетворяет условиям теоремы Банаха на всем пространстве, т.е.
удовлетворяет условиям теоремы Банаха на всем пространстве, т.е. 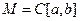 . На пространстве
. На пространстве 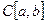 далее рассматривается макс-норма.
далее рассматривается макс-норма.
Теорема (существование единственности решения задачи Коши). Пусть выполнены условия
1) 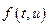 по второму аргументу удовлетворяет условию Липшица с константой
по второму аргументу удовлетворяет условию Липшица с константой 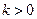 , т.е.
, т.е.
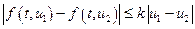 ,
, 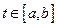
2) 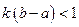 .
.
Тогда существует решение задачи коши (1). Это решение можно найти методом последовательных приближений интегрального уравнения (2).
Доказательство. Достаточно проверить, что оператор 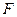 при произвольно фиксированном
при произвольно фиксированном 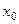 удовлетворяет условию Липшица с константой меньше единицы. Имеем
удовлетворяет условию Липшица с константой меньше единицы. Имеем
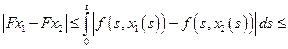
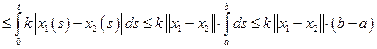
Перейдем в этом неравенстве к максимуму по 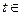
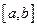 и получим:
и получим:
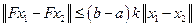
Так как 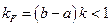 по условию теоремы, то оператор
по условию теоремы, то оператор 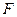 является сжимающим. По теореме Банаха
является сжимающим. По теореме Банаха 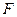 имеет единственную неподвижную точку, которая будет решением интегрального уравнения (2). Теорема доказана.
имеет единственную неподвижную точку, которая будет решением интегрального уравнения (2). Теорема доказана.
|
|