
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теорема Шаудера.
|
|
Рассмотрим уравнение 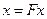 с непрерывным оператором
с непрерывным оператором 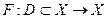 .
.
Теорема Шаудера. Пусть 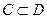 - непустое замкнутое выпуклое множество. Если выполнены условия:
- непустое замкнутое выпуклое множество. Если выполнены условия:
1. 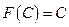 ;
;
2. 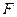 - вполне непрерывный оператор;
- вполне непрерывный оператор;
Следовательно, существует хотя бы одна неподвижная точка оператора 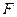 .
.
Примем теорему без доказательства.
На практике часто возникает необходимость построения выпуклого множества  . Рассмотрим утверждение (следствие теоремы Шаудера), в котором в качестве
. Рассмотрим утверждение (следствие теоремы Шаудера), в котором в качестве  выступает замкнутый шар с центром в
выступает замкнутый шар с центром в 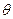 и некоторого радиуса
и некоторого радиуса 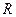 .
.
Следствие. Пусть вполне непрерывный оператор 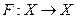 удовлетворяет неравенству
удовлетворяет неравенству
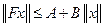 ,
, 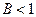 ,
,
следовательно, существует хотя бы одна неподвижная точка.
Неравенство в следствии является ограничением на скорость роста нелинейного оператора 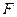 . Кроме того, это неравенство является аналогом условия Липшица на бесконечности.
. Кроме того, это неравенство является аналогом условия Липшица на бесконечности.
Для доказательства достаточно в силу теоремы Шаудера проверить, что неравенство обеспечивает существование такого замкнутого шара 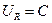 , такой что:
, такой что: 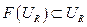 .
.
Зафиксируем радиус шара 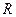 и рассмотрим неравенство
и рассмотрим неравенство
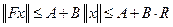 , где
, где 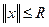 .
.
Это неравенство означает, что
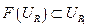 ,
,
где 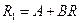 . Если
. Если 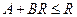 , то
, то 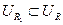 , следовательно, для данного радиуса выполняется требуемое вложение
, следовательно, для данного радиуса выполняется требуемое вложение 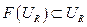 .
.
Рассмотрим зависимость 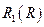 . Пусть существует
. Пусть существует 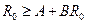 , следовательно, для данного радиуса выполняется
, следовательно, для данного радиуса выполняется 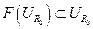 , следовательно, выполняются все условия теоремы Шаудера, то есть, вместе с вполне непрерывностью оператор
, следовательно, выполняются все условия теоремы Шаудера, то есть, вместе с вполне непрерывностью оператор 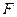 отражает непустое выпуклое замкнутое множество в себя
отражает непустое выпуклое замкнутое множество в себя 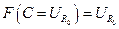 , следовательно, существует хотя бы одно решение системы (1), то есть, существует неподвижная точка.
, следовательно, существует хотя бы одно решение системы (1), то есть, существует неподвижная точка.
Следствие и теорема гарантируют существование неподвижной точки, но не обеспечивают её единственность.
Задача Коши для обыкновенного дифференциального уравнения первого порядка.
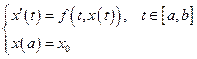
Функция  непрерывна. Как было показано, разрешимость данной задачи следует из разрешимости интегрального уравнения:
непрерывна. Как было показано, разрешимость данной задачи следует из разрешимости интегрального уравнения:
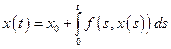 ,
,
которое представим в виде операторного уравнения 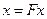 ,
, 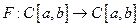 . Всякое непрерывное решение интегрального уравнения является непрерывным решением дифференциального уравнения задачи Коши.
. Всякое непрерывное решение интегрального уравнения является непрерывным решением дифференциального уравнения задачи Коши.
Для доказательства существования неподвижной точки оператора 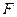 (а это в конечном счете означает, что задача Коши имеет хотя бы одно решение) воспользуемся утверждением следствия. Отметим, что из непрерывности функции двух переменных следует вполне непрерывность оператора
(а это в конечном счете означает, что задача Коши имеет хотя бы одно решение) воспользуемся утверждением следствия. Отметим, что из непрерывности функции двух переменных следует вполне непрерывность оператора 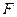 . Доказательство этого факта проводится с применением теоремы Арцела по той же схеме, что и доказательство вполне непрерывности интегрального оператора. Для доказательства существования неподвижной точки остается обеспечить выполнение неравенства в следствии. Для этого предположим, что функция
. Доказательство этого факта проводится с применением теоремы Арцела по той же схеме, что и доказательство вполне непрерывности интегрального оператора. Для доказательства существования неподвижной точки остается обеспечить выполнение неравенства в следствии. Для этого предположим, что функция 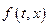 удовлетворяет неравенству:
удовлетворяет неравенству:
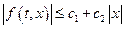 ,
,
Имеем
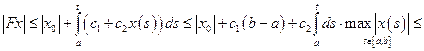
 ,
, 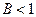
Теорема. Пусть выполнены условия:
1. 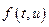 непрерывная функция;
непрерывная функция;
2. выполняется  ;
;
3.  ,
,
следовательно, задача Коши имеет хотя бы одно значение.
Отметим, что в этой теореме, как и в теореме о существовании единственности важное значение имеет произведение длин отрезков на константу 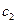 , поэтому в теории дифференциальных уравнений для данной задачи, что бы достичь условия существования или единственности регулируют длину промежутка. Такие утверждения называют локальными в отличии от полученных в данной главе глобальных.
, поэтому в теории дифференциальных уравнений для данной задачи, что бы достичь условия существования или единственности регулируют длину промежутка. Такие утверждения называют локальными в отличии от полученных в данной главе глобальных.
Отметим, что теоремы существования и существования единственности остаются, справедливы и при более слабых ограничениях на функцию двух переменных. Например, необязательно непрерывность 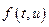 по переменной
по переменной  .,
.,
|
|