Материалы для изучения

Рассмотрим задачу оптимизации. Если в задаче оптимизации либо целевая функция, либо ограничения, либо и то, и другое нелинейны, то возникает задача нелинейного программирования.

Для нелинейных задач не существует методов, гаранти­рующих получение решения или вывода о его несуществова­нии, подобных симплекс-методу для линейных задач. Это неудивительно, поскольку даже в более простой, чем задача оптимизации, задаче решения нелинейного уравнения (сис­темы уравнений) также не существует таких методов.

Разумеется, это не означает невозможности решения каж­дой конкретной задачи нелинейного программирования. Однако гарантии успеха, даже в определении того, есть ли решение, в общем случае не существует.

Вернемся к рассмотренному выше примеру работы стан­ции технического обслуживания автомобилей, выполняю­щей два вида работ: ТО-1 и ТО-2. Изменим постановку зада­чи следующим образом: допустим, что прибыль, получаемая предприятием от производства работ, связана с ценой, взи­маемой с клиентов, по корневому закону: если цена услуги равна х, то прибыль пропорциональна 4х. Пусть целью ра­боты предприятия будет максимизация прибыли. Тогда мы имеем ту же систему ограничений:

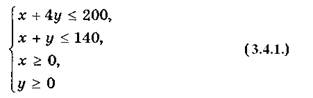
и следующую целевую функцию:

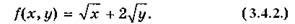
значений, но не в вершине многоугольника, а в точке Р, ле­жащей на одной из сторон.

Координаты точки Р можно найти следующим образом. Поскольку в этой точке прямая АВ касается линии уровня, а при меньших значениях целевой функции дважды ее пере­секает, то надо найти условие, при котором две точки пере­сечения переходят в одну. Составим систему уравнений со­ответствующих линий:

Ситуацию с этой задачей иллюстрирует рис. 3.4.1.

Рис. 3.4.1. Иллюстрация к решению задачи

На нем изображена область допустимых решений (многоугольник ABCD) и три линии уровня целевой функции. Как и прежде (при решении аналогичной линейной задачи) максимум це­левой функции реализуется на границе области допустимых

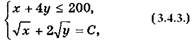
где С — значение целевой функции. На рис. 3.4.1 линии уров­ня целевой функции соответствуют следующим ее значениям: 1) С = 22; 2) С = 26, 46; 3) С = 30. Решая систему (3.4.3), полу­чаем квадратное уравнение для нахождения х (или у), в кото­рое в качестве параметра входит С. Ситуация наличия двух действительных корней этого уравнения переходит с ростом С в ситуацию наличия одного корня и далее — в ситуацию от­сутствия корней. Условие наличия одного корня — равенство нулю дискриминанта указанного квадратного уравнения. Это событие реализуется при С = 20. Соответствующие решения системы уравнений (3.4.3): х = 100, у = 25.