
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Интегрирование рациональных дробей
|
|
Отношение двух многочленов, где
Pm (x) = am xm + am– 1 xm– 1 + … + a 2 x 2 + a 1 x + a 0,
Qn (x) = bn xn + bn– 1 xn– 1 + … + b 2 x 2 + b 1 x + b 0,
есть рациональная дробь. Рациональная дробь называется правильной, если степень многочлена в числителе меньше степени многочлена в знаменателе, т.е. m< n. В противном случае, разделив числитель на знаменатель, получим сумму многочлена и правильной дроби.
Правильную рациональную дробь можно разложить на сумму простейших дробей четырех типов:
1-й тип:; 2-й тип:; 3-й тип:; 4-й тип:,
где A, B, C, D, E, F – действительные числа. При этом a – корень Qn (x), т.е. k – натуральное число, не превосходящее кратности корня a; x 2 +px+q – квадратный трехчлен с отрицательным дискриминантом: этому трехчлену соответствуют комплексно сопряженные корни Qn (x), s – натуральное число, не превосходящее кратности этих комплексно-сопряженных корней.
Разложив рациональную дробь на простейшие, переходят к интегрированию. Интегрирование простейших дробей 1-го и 2-го типов сводится к применению табличных интегралов:
ò dx = A× ln | x – a | + C;
ò dx = B × ò (x – a)– k dx = (x – a)1– k + C.
Интегрирование простейших дробей 3-го и 4-го типов проиллюстрируем на примерах. При этом отметим, интегралы от рациональных дробей всегда можно вычислить, и первообразные представляют собой элементарные функции.
Пример 1. Найти интеграл ò.
Решение. Подынтегральную рациональную дробь разлагаем на элементарные дроби:
= = + +,
(дискриминант трехчлена x 2–4 x +5 отрицательный). В разложении фигурируют дроби 1-го, 2-го и 3-го типов. Определим коэффициенты A, B, C, D, для чего приводим сумму справа к общему знаменателю, а затем приравниваем числитель справа к числителю слева:
A (x –2)(x 2 – 4 x + 5) + B (x 2 – 4 x + 5) + (Cx + D)(x –2)2 = A (x 3 – 6 x 2 + 13 x – 10) +
+ B (x 2 – 4 x + 5) + (Cx 3 – 4 Cx 2 + 4 Cx + Dx 2 – 4 Dx + 4 D) = (A+C) x 3 +
+ (–6 A + B – 4 C + D) x 2 + (13 A – 4 B + 4 C – 4 D)x + (–10 A + 5 B + 4 D) = 1,
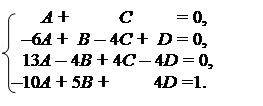 |
откуда получаем систему четырех линейных уравнений
Решая эту систему, получаем A = C = 0, B = 1, D = –1. Итак,
ò = ò [– ] dx =
= – – ò dx = – – arctg(x –2) + C.
Пример 2. Найти интеграл ò dx.
Решение. Представим подынтегральную функцию в виде суммы элементарных дробей, причем в разложение будут входить лишь дроби 3-го и 4-го типов, поскольку дискриминант квадратного трехчлена x 2 + 2 x + 2 отрицательный:
= +.
Если правую часть этого равенства привести к общему знаменателю, то числитель для полученной дроби примет вид
(Ax + B)(x 2 + 2 x + 2) + Cx + D = Ax 3 + (2 A+B) x 2 + (2 A +2 B + C) x + (2 B+D).
Этот многочлен с неопределенными коэффициентами A, B, C, D должен быть равен x 2, откуда следует: A =0, B =1, C=D = –2. Таким образом,
ò dx = ò [ – 2× ] dx =
= ò – ò dx.
Легко видеть, что arctg(x +1) –первообразная для функции. Если в интеграле ò dx ввести новую переменную t = (x +1)2 +1, то с учетом равенства dt = 2(x+ 1) dx, получаем ò dx = ò и – = – – первообразная для. Окончательно получаем
ò dx = arctg(x +1) + + C;
|
|