
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Алгоритм переходу від ззлп до СЗЛП.
|
|
Переходу від загальної задачі лінійного програмування до стандартної задачі лінійного програмування здійснюється просто.
ü Якщо в задачі лінійного програмування йде мова про максимізацію лінійної форми (цільової функції), то достатньо розглядати лінійну форму з протилежним знаком: 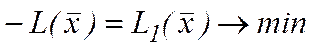 .
.
ü Якщо в умовах, які накладаються на змінні, присутні нерівності типу:  для деякого і, то легко перейти до рівності, ввівши додаткову (нову) змінну
для деякого і, то легко перейти до рівності, ввівши додаткову (нову) змінну 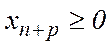 таким чином:
таким чином: 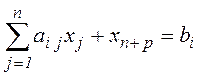 .
.
ü Якщо в умовах, які накладаються на змінні, присутні нерівності типу:  для деякого і, то легко перейти до рівності, ввівши додаткову (нову) змінну
для деякого і, то легко перейти до рівності, ввівши додаткову (нову) змінну 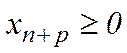 таким чином:
таким чином: 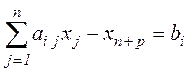 .
.
Зауваження. Очевидно, що при введені додаткових змінних збільшується розмірність задачі.
ü Якщо при деякому j змінна 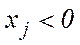 , то її можна представити у вигляді двох невід’ємних змінних:
, то її можна представити у вигляді двох невід’ємних змінних:  , де
, де 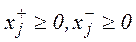 .
.
Загальний вигляд канонічної задачі:
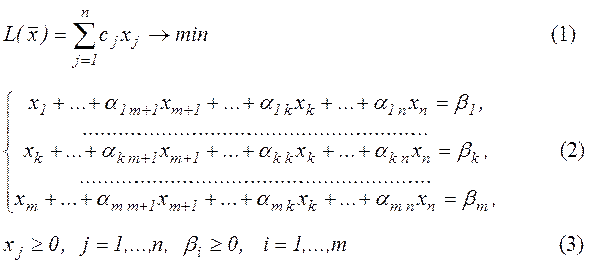
Канонічна задача лінійного програмування в матричній формі має вигляд:
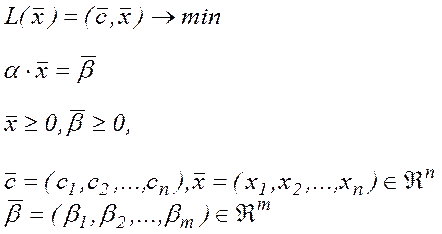

Для такої задачі лінійного програмування можна зразу вказати один із опорних планів. Оптимальним планом є такий вектор:  . Цей вектор задовольняє умови (2) і (3). Крім того, m першим компонентам відповідає лінійно-незалежна система векторів.
. Цей вектор задовольняє умови (2) і (3). Крім того, m першим компонентам відповідає лінійно-незалежна система векторів.
Розглянемо теоретичну можливість переходу від стандартної задачі лінійного програмування до канонічної.
Нехай 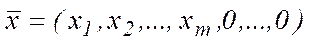 якому відповідає базисна матриця
якому відповідає базисна матриця  . Помножимо
. Помножимо 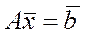 на
на 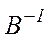 зліва. Отримаємо
зліва. Отримаємо  , тоді будемо мати такий вигляд
, тоді будемо мати такий вигляд 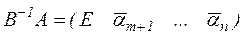 , крім того
, крім того  .
.
Критерій оптимальності. Якщо існує базисний розв’язок канонічної задачі лінійного програмування 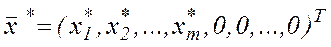 і
і 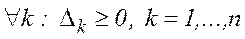 , то
, то 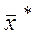 – оптимальний план задачі. Де
– оптимальний план задачі. Де 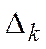 – відносна оцінка, яка обчислюється по формулі
– відносна оцінка, яка обчислюється по формулі  , причому відносні оцінки для базисних змінних рівні нулю.
, причому відносні оцінки для базисних змінних рівні нулю.
Ознака необмеженості цільової функції знизу. Якщо серед відносних оцінок деякого базисного плану задачі лінійного програмування існує від’ємна ( ), а серед компонент k -ого стовпчика немає додатних коефіцієнтів (
), а серед компонент k -ого стовпчика немає додатних коефіцієнтів ( ), то лінійна форма (цільова функція)
), то лінійна форма (цільова функція) 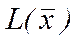 – необмежена знизу на допустимій множині.
– необмежена знизу на допустимій множині.
Для розв’язання канонічної задачі лінійного програмування застосовуємо симплекс-метод.
|
|