Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Модель аналітичного групування.

Важливішою кількісною характеристикою кореляційного зв’язку є так звана лінія регресії. Лінією регресії “y” на “x” називається функція, що зв’язує умовні середні значення результативної ознаки з індивідуальними значеннями факторної ознаки.

Лінія регресії як і функція може мати 3 зображення:

1)графічне;

2)таблиичне;

3)аналітичне.

Графічне зображення самостійної ролі у вивченні взаємозв’язків немає.

На табличному зображенні базується метод аналітичного групування або модель аналітичного групування.

Побудова і аналіз МАГ передбачає вирішення таких завдань:

а) теоретичне обгрунтування моделі;

б) оцінка лінії регресії;

в) вимірювання тісноти зв’язку;

г) перевірка зв’язку;

Обгрунтувати модель – це значить здійснити глибокий теоретичний аналіз суті явища, що вивчається і визначити таким чином основні факторні ознаки, що можуть впливати на певну результативну ознаку, яка цікавить дослідника.

На цьому етапі визначається кількість груп та розмір інтервалу.

Слід мати на увазі, що аналітичне групування здійснюється завжди за факторною ознакою.

Оцінити лінію регресії – це значить обчислити середнє значення результативної ознаки по кожній з відокремлених груп за факторною ознакою.

МАГ може бути одно-, дво-, трьо-факторною.

Уявімо собі, що метою нашого дослідження є вивчення залежності середнього доходу на кожного члена сім’ї в сім’ях службовців в залежності від їх розміру

Цілком очевидно, що середньодушовий доход в певній мірі залежить від числа членів сім’ї.

Таким чином перша з названих ознак результативна, друга – факторна. Засобом, що дозволить довести це припущення про наявність залежності є модель аналітичного групування. Розглянемо схему вивчення ціє залежності на прикладі даних, що отримані в результаті вибіркового опитування 50-ти сімей службовців одного з регіонів (січень 1997 р.).

Дле того, щоб виявити чи існює залежність між обраними ознаками, слід побудувати аналітичні групування.

Як бачимо, значення факторної ознаки Х₁=1, Х₂=2,..., Х₅=5. В цьому випадку беззаперечно є розподіл (об’єднання) елементів сукупності за факторною ознакою на 5 груп. Виділивши 5 груп також обчислити середні значення рівні результативні ознаки по кожній з виділених груп:

Результати занесемо в таблицю.

Таблиця. Залежність середньодушового доходу від розміру сім’ї.

Розмір сім’ї (x)	Кількість сімей (fi)	Середньодушовий доход по групах тис.крб. ()
Разом		Х

Як бачимо, дані цього аналітичного групування підтверджують гіпотезу про наявність зв’язку між досліджуваними ознаками: чим більша сім’я, тим нищий середньодушовий доход на 1 члена сім’ї.

Зобразимо цю залежність графічно.

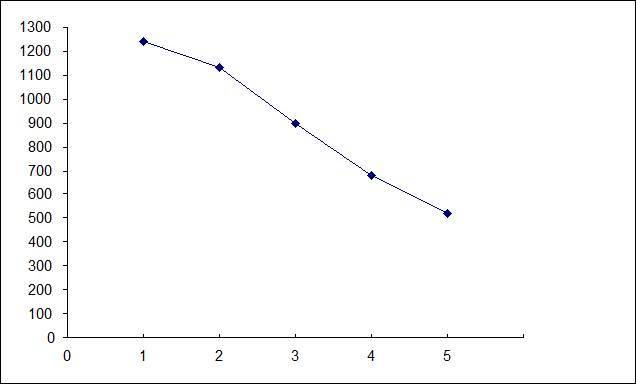
Лінія регресії в цьому конкретному випадку характеризує залежність середніх значень доходу в розрахунку на члена сім’ї від кількості членів сім’ї в окремих точках.

Вона не описує в повній мірі об’єктивний зв’язок, але чим більше “n”, тим точніша ця оцінка.

Третім етапом вимірювання зв’язку є оцінка тісноти зв’язку.

Обчислення характеристики, що дозволяє оцінити тісноту зв’язку базується на математичному правилі складання дисперсій або варіацій.

Це правило можна записати так: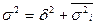

Розглянемо економічний зміст кожної з цих дисперсій

. Загальна дисперсія () характеризує міру варіації (відхилень індивідуальних значень результативної ознаки від середнього значення по сукупності) результативної ознаки “y”, що пов’язана (зпричинена) усіма без винятку факторами, що могли вплинути на, варіацію результативної ознаки. Обчислюється за формулами

;

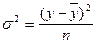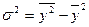
Для нашого прикладу ця дисперсія становить =1875.

Загальна середня результативної ознаки, тобто середньодушовий доход за 50 сім’ях вцілому становить =90 грн. Загальна дисперсія 1875 характеризує міру варіації середньодушового доходу, спричинену впливом таких факторів, як розмір сім’ї, кількість працюючих, посади працюючих, освіта і т.д.

Якщож обчислити дисперсію по кожній з груп, то отримаємо характеристики міри варіації результативної ознаки на яку не впливає групувальна ознака або обраний для вивчення фактор (розмір сім’ї).

Групові дисперсії обчислюються за формулою

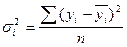
де y_i – індивідуальні значення результуючої ознаки по кожній з груп;

– середні значення результуючої ознаки по кожній з груп.

Узагальнюючою характеристикою цих дисперсій є середнє з них

середня з групових:

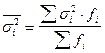
Випадкова або залишкова дисперсія, бо вона характеризує міру варіації результуючої ознаки, спричинену рештою факторів, крім головного фактору, покладеного в основу груповань.

Міру варіації результуючої ознаки, спричинену головним фактором “x” характеризує так звана міжгрупова дисперсія:

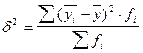
– середня по сукупності в цілому ( =90 грн.)

Варіацію результивної ознаки, обумовлену виявом головного фактора часто називають систематичною або факторною.

Обчилимо міжгрупову дисперсію за даними наведеного вище аналітичного груповання

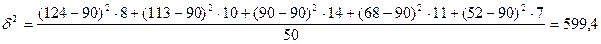
Співвідношення міжгрупової і загальної дисперсією харакрактеризує тісноту кореляяційного зв’язку і називається кореляційним відношенням.

.

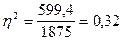
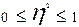Висновок: Таким чином варіація середньодушового доходу по обстежених 50-ти сім’ях на 32% спричинена варіацією числа членв сім’ї

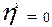кореляційний зв’язок відсутній 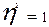функціональний зв’язок

Важливим етапом вивчення кореляціного зв’язку є перевірка суттєвості (істотності) зв’язку. Перевірити істотність зв’язку – це значить переконатись, що кореляційна залежність виявлена на основі аналітичного групування не є випадковою фактичне значення кореляційного відношення з критичним цього показника.

Критичне значення це таке його максимально можливе значення, яке могло виникнути при випадковому зв’язку між ознаками y і x або при такому незначному зв’язку, яким можна знехтувати.

Критичні значення , що є в спеціальних таблицях обчислені для заданих рівнів істотності і відповідних чисел ступенів свободи (k)

Рівень істотності – ймовірність отримання значення більшого за критичне при умові відсутності зв’язку між ознаками.

Якщо 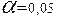, то це значить, що дане табличне значення не з’явиться в п‘яти випадках із ста, і якщо 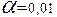, то в одному випадку із ста.

Числом ступені свободи називається число незалежних змінних необхідних для обчислення того чи іншого показника.

Так для обчислення k=n-1 для

x1=10; x2=12; x3=8 =10

n – число елементів сукупності.

Число ступенів свободи для дисперсій обчислюється так

k1=m-1 для (при відсутності зв’язку між признаками тільки в 5 випадках з 100 більше критичного значення )

k2=n-m для m – число груп аналітичного групування.

Якщо критичне < фактичне, то кореляційний зв’язок признається істотним.

Перевіримо істотність зв’язку для наведеного вище прикладу. Перевіримо його для рівня істотності 0, 05. Обчислимо число ступенів свободи

k1=m-1=5-1=4

k2=n-m=50-5=45.

Знаходимо по таблиці критичне значення при заданих умовах

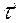критичне=0, 207

Фактичне значення , тобто обчислення коли на основі складення дисперсій становило 0, 335. Порівнявши критичне з фактичне робимо висновок, що зв’язок між середньодушовим доходом і розміром сім‘ї є істотним.

Перевірку істотності зв’язку можна здійснити також скориставшись іншим показником, що що називається критерієм Фішера

Fкритерій=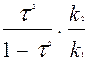

F= .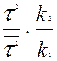

Значення Fкритич. також є в спеціальних таблицях. Перевірка суттєвості за цим критерієм аналогічна перевірці, що здійснюється з допомогою 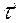.