
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Линейная регрессия
|
|
Пусть (X, Y) — двумерная случайная величина, где X и Y — зависимые случайные величины. Оказывается возможным приближенное представление величины Y в виде линейной функции величины X:
 (24)
(24)
где а и b — параметры, подлежащие определению. Обычно эти величины определяются с помощью метода наименьших квадратов.
Функция 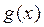 называется среднеквадратической регрессией Y на X
называется среднеквадратической регрессией Y на X
Линейная средняя квадратическая регрессия Y на X имеет вид
 , (25)
, (25)
где  определяется формулой (22), ту = М (Y) и тx = М (X) — математические ожидания, соответственно, случайных величин Y и X.
определяется формулой (22), ту = М (Y) и тx = М (X) — математические ожидания, соответственно, случайных величин Y и X.
Коэффициент b = 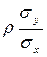 называют коэффициентом регрессии Y на X, а прямую, реализующую линейную зависимость (25) случайной величины Y от случайной величины X,
называют коэффициентом регрессии Y на X, а прямую, реализующую линейную зависимость (25) случайной величины Y от случайной величины X,
 (26)
(26)
– прямой среднеквадратической регрессии Y на X. Поскольку зависимость (26) является приближенной, то существует погрешность итога приближения, называемая остаточной дисперсией:
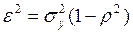 (27)
(27)
Для оценки среднеквадратичной погрешности линейной регрессии обычно используют величину  .
.
|
|