
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Собственные числа и собственные векторы матриц
|
|
Второй наиболее часто встречающейся задачей линейной алгебры является задача поиска собственных чисел и собственных векторов заданной квадратной матрицы. Нахождение собственных чисел эквивалентно задаче решения СЛАУ вида:
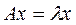
Эта однородная система линейных уравнений имеет решения для конкретных значений - λ 1, λ 2, …., которые называются собственными числами матрицы системы А. Каждому собственному числу соответствует собственный вектор – х1, х2, ….., который является решением системы для данного собственного числа. Таким образом, для того, чтобы знать полный набор решений, необходимо определить собственные числа матрицы системы и найти для них соответствующие собственные векторы.
Для решения таких задач на собственные числа и собственные векторы существует несколько встроенных функций, реализующих достаточно сложные вычислительные алгоритмы:
- eiganvals(A) – вычисляет вектор собственных чисел;
- eigenvecs(A) – вычисляет матрицу, содержащую нормированные собственные векторы, каждый столбец включает в себя координаты одного собственного вектора, количество столбцов равно количеству собственных чисел;
- eigenvec(A, λ) – вычисляет один собственный вектор для заданного собственного числа.
Доступ к этим функциям осуществляется через панель инструментов и диалоговое окно (рис.16):
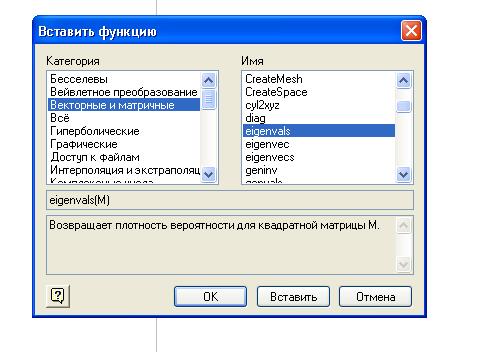
Проиллюстрируем применение этих функций на примерах.
Примеры.
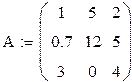
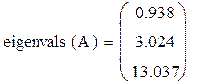
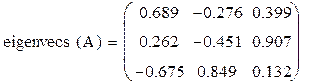

|
|