Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства математического ожидания
|
|
1) 
, т.к.
Доказательство:
| X | С |
| P | 1 |
.
2) 
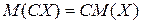
Доказательство:
Пусть
| X | x1 | x2 | x3 | … | xn |
| P | p1 | p2 | p3 | … | pn |
тогда
| СX | Сx1 | Сx2 | Сx3 | … | Сxn |
| P | p1 | p2 | p3 | … | pn |
Вычислим мат. ожидание
.
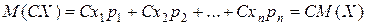3) 
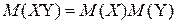, где 
и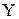 
независимые случайные величины.
Доказательство:
Пусть
| X | x1 | x2 |
| P | p1 | p2 |
| Y | y1 | y2 |
| P | g1 | g2 |
тогда
| XY | x1 y1 | x2 y1 | x1 y2 | x2 y2 | - возможные значения |
| P | p1 g1 | p2 g1 | p1 g2 | p2 g2 | - их вероятности |
4) 
, где и 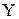необязательно независимые случайные величины, могут быть и зависимыми.
Доказательство:
Пусть
| X | x1 | x2 |
| P | p1 | p2 |
| Y | y1 | y2 |
| P | g1 | g2 |
тогда
| X+Y | x1 +y1 | x2 +y1 | x1 +y2 | x2 +y2 |
| P | p11 | p21 | p12 | p22 |
Ясно, что
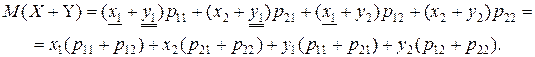
Докажем, что 
. Пусть событие принимает значение
x1 +y1 или x1 +y2.
Значит, вероятность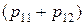 
- это вероятность наступления события x1, т.е. 
.
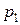Аналогично,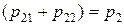 
, 
, 
.
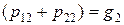Значит,
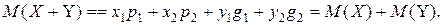
Следствие: 
.
Примеры: 1. Производится 3 выстрела с вероятностями попадания в цель 
; 
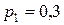и 
. Найти мат.ожидание общего числа попадания.
Решение: Пусть X1 – число попаданий при первом выстреле,
X2 – число попаданий при втором выстреле,
X3 – число попаданий при третьем выстреле.
| X1 | 1 | 0 |
| P | 0, 4 | 1-0, 4 |
| X2 | 1 | 0 |
| P | 0, 3 | 0, 7 |
| X3 | 1 | 0 |
| P | 0, 6 | 0, 4 |
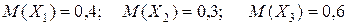
- общее число попаданий.
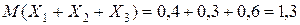попаданий.
2. Найти мат.ожидание суммы числа очков, которые могут выпасть при бросании двух игральных костей.
Решение: Пусть X1 – число очков на первой кости,
X2 – число очков на второй кости.
| X1 | 1 | 2 | 3 | 4 | 5 | 6 |
| P |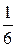 
|
|
|
|
|
|
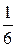
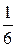
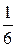
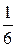
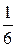
| X2 | 1 | 2 | 3 | 4 | 5 | 6 |
| P |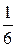
|
|
|
|
|
|
;
;
.
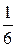
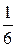
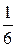
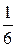
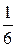
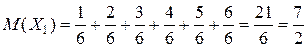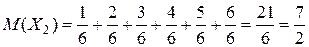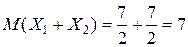II. Дисперсия дискретной случайной величины D(X).
Пример:
| X1 | -0, 01 | 0, 01 |
| P | 0, 5 | 0, 5 |
| X2 | -100 | 100 |
| P | 0, 5 | 0, 5 |
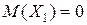и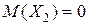 
.
Здесь мат.ожидания обеих величин одинаковы, а возможные значения различны, причем X1 имеет возможные значения, близкие к мат.ожиданию, а X2 - далекие от своего мат.ожидания. Т.е. зная лишь мат.ожидание случайной величины, нельзя судить ни о том, какие возможные значения она может принимать, ни о том, как они рассеяны вокруг мат.ожидания.
Пусть X – случайная величина и M(X) ее мат.ожидание. Рассмотрим отклонение X-M(X).
Пусть
| X | x1 | x2 | x3 | … | xn |
| P | p1 | p2 | p3 | … | pn |
Тогда
| X-M(X) | x1-M(X) | x2-M(X) | x3-M(X) | … | xn-M(X) |
| P | p1 | p2 | p3 | … | pn |
Т.к. для того, чтобы отклонение приняло значение x1-M(X) достаточно, чтобы случайная величина приняла значение x1. Вероятность же этого события p1.
Теорема: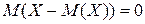 
.
Доказательство:
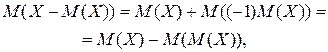
Т.к.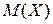 
- постоянная величина, то 
. (
)
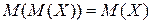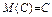Значит,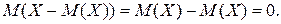 
На практике часто требуется оценить рассеяние возможных значений случайной величины вокруг ее среднего значения (например, насколько кучно лягут снаряды вблизи цели). Но отклонение для этого не подойдут, т.к. среднее значений отклонений 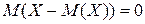, поэтому вводят понятие дисперсии.
Определение: Дисперсией (рассеянием) дискретной случайной величины называют мат.ожидание квадрата отклонения случайной величины от ее мат.ожидания, т.е.
.
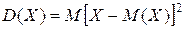Пусть
| X | x1 | x2 | x3 | … | xn |
| P | p1 | p2 | p3 | … | pn |
Тогда
| [X-M(X)]2 | [x1-M(X)]2 | [x2-M(X)]2 | [x3-M(X)]2 | … | [xn-M(X)]2 |
| P | p1 | p2 | p3 | … | pn |
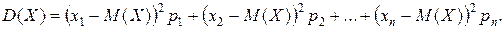
Пример:
| X | 1 | 2 | 5 |
| P | 0, 3 | 0, 5 | 0, 2 |
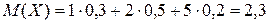
[x1-M(X)]2=(1 - 2, 3)2=1, 69;
[x2-M(X)]2=(2 - 2, 3)2=0, 09;
[x3-M(X)]2=(5 - 2, 3)2=7, 29
| [X-M(X)]2 | 1, 69 | 0, 09 | 7, 29 |
| P | 0, 3 | 0, 5 | 0, 2 |
.
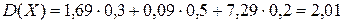Вычисления громоздки, чаще используют другую формулу для вычисления дисперсии.
Теорема: 
.
Доказательство:
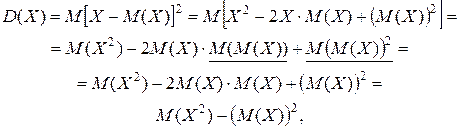
Т.к. 
- константы.
Пример:
| X | 1 | 2 | 5 |
| P | 0, 3 | 0, 5 | 0, 2 |
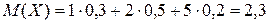
| X2 | 1 | 4 | 25 |
| P | 0, 3 | 0, 5 | 0, 2 |
|
|
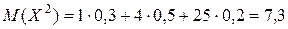