Получение случайных чисел, подчиняющихся экспоненциальному закону

Рассмотрим в качестве примера получение случайного числа с экспоненциальным распределением. Это распределение характеризуется одним параметром λ > 0 и имеет следующие функции распределения и плотности распределения:

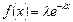, x ≥ 0;

Для этого распределения легко получить F ^–1 (y), т.е. разрешить уравнение F (x)= y. Решение имеет вид

.

Для получения x с искомым распределением нужно сгенерировать y, равномерно распределенное на (0, 1), и применить эту формулу. Если говорить о практической стороне дела, то существуют более эффективные способы, в которых не используется медленная операция вычисления логарифма для каждого случайного числа. Данный способ продемонстрирован лишь как пример более общего подхода с использованием обратной функции распределения.

моделирование экспоненциальной случайной величины

Как известно, случайная величина x, распределенная по экспоненциальныму закону описывается следующей плотностью распределения:

На рис. 1 построены графики экспоненциальных плотностей распределения при различных значениях параметра λ.

с разными значениями параметра

Экспоненциальному распределению, как правило, подчиняется случайный интервал времени τ между поступлениями заявок в систему массового обслуживания. Поэтому весьма важно уметь моделировать потоки заявок разной интенсивности λ.

Напомним, что математическое М[τ ] ожидание экспоненциально распределенной случайной величины τ равно

Чтобы найти алгоритм имитации экспоненциально распределенных чисел τ, применим метод инверсии:

Откуда

но, поскольку случайная величина (1 - R) распределена точно так же, как R, и находится в том же интервале (0, 1), то (9) можно заменить на более удобную формулу:

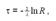что дает искомый ответ.

12. моделирование случайных объектов. Квазиравномерное распределение.

При моделировании процессов и сист.исп-ся 3 вида случ.объектов. 1.сл.величины, 2.сл.события, 3.сл.процессы. Случайная величина 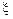, имеющая квазиравномерное распределение в интервале [0, 1], принимает значения с вероятностями .

Математическое ожидание и дисперсия квазиравномерной СВ соответственно имеют вид:

, .

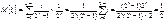В первом случае используем соотношение: . (20)

Во втором случае имеем соотношение: . (21)

Таким образом, математическое ожидание квазиравномерной случайной величины совпадает с математическим ожиданием равномерной случайной последовательности интервала [0, 1], а дисперсия отличается множителем (2 ⁿ + 1) / (2 ⁿ – 1), который при достаточно больших n близок к единице.

На ЭВМ невозможно получить идеальную последовательность случайных чисел, т.к. можно оперировать только с конечным множеством чисел, и для получения значений х случайной величины используют формулы; поэтому такие последовательности называют псевдослучайными.

Способы получ.квазир.сл.чисел: 1.при помощи спец.таблиц, 2.при помощи физич.датчиков (рулетки, ген.шумов и др). 3. Спец.прогр.датчики получения квазиравн.случ.чисел. 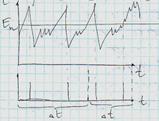. если число ипульсов четное, то выход 0 и наоборот.получалась последовательность, что дает достаточно высокую случайность для бульшой разрядной сетки. Особенность физ.датчиков в том, что случ.послед-ть которую они создают-повторить невозможно. Прогр.датчики .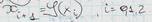