
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
i , j ,k так, что бы вектор i совпал с ортом e оси .
|
|
a =a 1 i + a 2 j+ a 3 k, b =b 1 i + b 2 j+ b 3 k.
Тогда
a + b = (a 1 +b 1) i + (a 2 +b2) j+ (a 3 +b3) k.
В силу единственности разложения по базису и равенства
a + b = (Пр i (a + b)) i + (Пр j (a + b)) j + (Пр k (a + b)) k
получим
Пр i (a + b) = a 1 +b 1= Пр i a+ Пр i b.
1.4. Скалярное произведение двух векторов, его свойства и выражение через координаты сомножителей
Определение. Скалярным произведением векторов 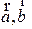 называется число, равное произведению их модулей на косинус угла между этими векторами. Обозначается скалярное произведение
называется число, равное произведению их модулей на косинус угла между этими векторами. Обозначается скалярное произведение 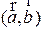
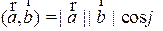 =
= 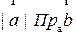 .
.
Отсюда, в частности, следует, что
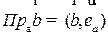 , где
, где 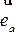 - орт вектора
- орт вектора 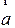 .
.
Непосредственно из определения следуют следующие свойства скалярного произведения:
1) 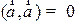 тогда и тольго тогда, когда
тогда и тольго тогда, когда 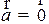 .
.
2) 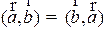 .
.
3)  .
.
Из свойства линейности проекции следует:
4) 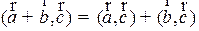 .
.
Действительно, 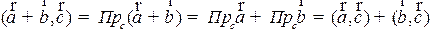 .
.
Выражение скалярного произведения в ортонормированном базисе.
Рассмотрим ортонормированный базис e 1, e 2, e 3 и два вектора
x =x 1 e 1 + x 2 e 2 + x 3 e 3, y =y 1 e 1 + y 2 e 2 + y 3 e 3, или, кратко, x = (x 1, x 2, x 3), y = (y 1, y 2, y 3). Тогда скалярное произведение будет равно:
(x, y) = (x 1 e 1 + x 2 e 2 + x 3 e 3, y 1 e 1 + y 2 e 2 + y 3 e 3)= x 1 y 1 + x 2 y 2 + x 3 y 3.
Для доказательства этого необходимо раскрыть скобки, используя свойства 2), 3) скалярного произведения и свойство ортонормированного базиса:
(e k, e m)= 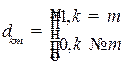 . Символ
. Символ 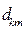 называется символом Кронекера.
называется символом Кронекера.
Теорема. Для равенства двух векторов необходимо и достаточно, чтобы проекции этих векторов на любую ось совпадали.
Необходимость следует из формулы Пр e 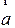
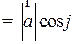 . Достаточност следует из равенств:
. Достаточност следует из равенств:
a = (Пр i a) i + (Пр j a) j + (Пр k a) k = (Пр i b) i + (Пр j b) j + (Пр k b) k=b.
1.5. Определители второго и третьего порядка. Решение систем. Правило Крамера. Векторное произведение двух векторов, его свойства и выражение через координаты сомножителей
1.5.1. Определители второго и третьего порядка.
Матрицей типа 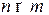 называется прямоугольная таблица из чисел, выстроенных в
называется прямоугольная таблица из чисел, выстроенных в 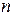 строк и
строк и 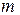 столбцов.
столбцов.
Примеры матриц 2x3, 3x1: 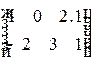 ,
,  .
.
В общем случае матрицу записывают, используя индексы для нумерации строк и столбцов:
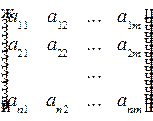 .
.
Матрица
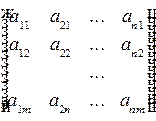
называется транспонированной матрицей для исходной матрицы.
Если 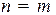 , то матрица называется квадратной. Важной характеристикой квадратной матрицы является определитель. Здесь мы ограничимся рассмотрением определителей матриц втрого и третьего порядков.
, то матрица называется квадратной. Важной характеристикой квадратной матрицы является определитель. Здесь мы ограничимся рассмотрением определителей матриц втрого и третьего порядков.
Определитель матрицы 2x2: 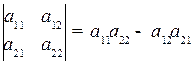 . .
| Определитель матрицы 3x3: 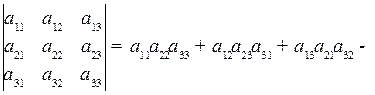 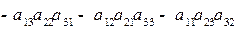 . .
| |
Slide_1_15 «Определители 2-го и 3-го порядков»
Схема вычисления слагаемых для определителя третьего порядка (рис. 1.15).
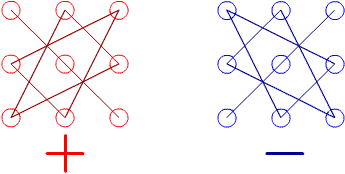
Рис. 1.15. Вычисление определителя
Квадратная матрица называется вырожденной, если ее определитель равен нулю.
Разложение определителя по первой сторке.
Для вычисления определителя третьего порядка удобно пользоваться следующей формулой разложения:
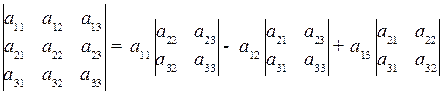 .
.
Slide_1_15_2 «Разложение определителя по строке»
Для элементов перовой строки 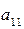
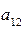
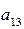 множителями служат
множителями служат
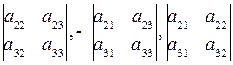 ,
,
которые называются алгебраическими дополнениями соответствующих элементов первой строки.
1.5.2.Решение систем. Правило Крамера
Решение системы
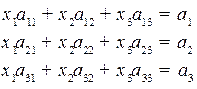
с невырожденной матрицей коэффициентов 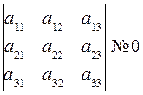 является единственным и находится по правилу Крамера:
является единственным и находится по правилу Крамера:
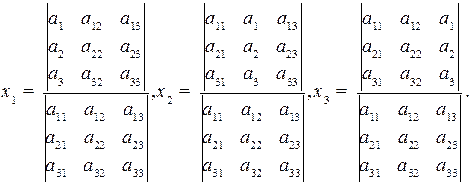
Slide_1_15_1 «Правило Крамера»
1.5.3. Векторное произведение
Тройка некомпланарных векторов a, b, c называется правой, если при приведении их к общему началу поворот от a к b по кратчайшему пути проводится против часовой стрелки, если смотреть из вершины вектора c. В противном случае, тройка векторов a, b, c называется левой.
Векторным произведением векторов a, b называется вектор c, удовлетворяющий условиям:
1)  с
с  =
=  a
a 
 b
b 
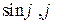 , -угол между векторами a, b,
, -угол между векторами a, b,
2) с 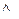 a, с
a, с 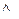 b,
b,
3) тройка a, b, c - правая (см. рис. 1.16)
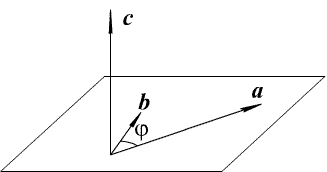
Рис. 1.16. Векторное произведение
Векторное произведение обозначается: с = [ a, b ].
Slide_1_16 «Векторное произведение»
Из определения следуют простейшие свойства векторного произведения:
Условие коллинеарности двух векторов a, b можно записать в виде:
[ a, b ] = 0.
Модуль векторного произведения [ a, b ] равен площади параллелограмма, построенного на векторах a, b ( см. рис. 1.17).
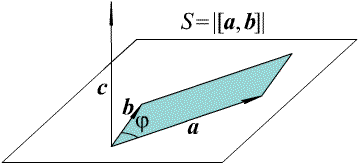
Рис. 1.17. Модуль векторного произведения
Slide_1_17 «Модуль векторного произведения»
Докажем, что векторное произведение обладает следующими свойствами:
1) [ a, b ] = -[ b, a ] (см. Рис. 1.18),
2) [  a, b ] =
a, b ] =  [ a, b ],
[ a, b ],
3) [ a+с, b ] = [ a, b ]+ [ с, b ] (см. Рис. 1.19).
Первое свойство следует из определения (если тройка a, b, c - правая, то правой будет тройка b, a, - c. см. рисунок).
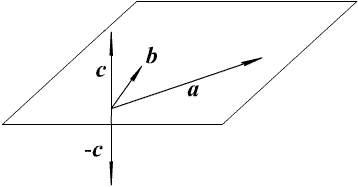
Рис. 1.18. Антикоммутативность
Slide_1_18 «Антикоммутативность векторного произведения»
Для доказательства второго и третьего свойств, обозначим через e единичный вектор, лежащий в плоскости векторов a, b (a, b – приведены к общему началу), перпендикулярный вектору b и такой, что тройка векторов ebc правая, а через g – орт вектора с = [ a, b ], g = с  с
с  (см. рисунок).
(см. рисунок).
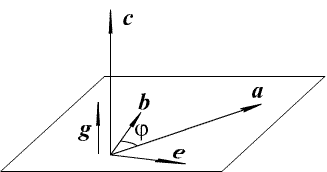
Рис. 1.19. Линейность
Тогда
[ a, b ]=  b
b  (Прe a) g (3)
(Прe a) g (3)
Действительно: [ a, b ]=  [ a, b ]
[ a, b ]  g =
g =  a
a 
 b
b 
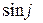 g =
g =  b
b  (Прe a) g.
(Прe a) g.
Из (3) получим свойство 2):
[  a, b ]=
a, b ]=  b
b  Прe (
Прe ( a) g =
a) g = 
 b
b  (Прe a) g =
(Прe a) g =  [ a, b ].
[ a, b ].
Аналогично выводится свойство 3):
[ a+с, b ] =  b
b  Прe (a+с) g =
Прe (a+с) g =  b
b  Прe a g+
Прe a g+  b
b  Прe с g = [ a, b ]+ [ с, b ].
Прe с g = [ a, b ]+ [ с, b ].
Slide_1_19 «Линейность векторного произведения»
Выражение векторного произведения через координаты векторов сомножителей в декартовой системе координат.
Пусть в декартовом базисе (i, j, k) выполнены разложения векторов:
x =x 1 i + x 2 j + x 3 k, y =y 1 i + y 2 j + y 3 k.
Используя свойства 1)-3) векторного произведения и равенства
k = [ i, j ], j = [ k, i ], i = [ j, k ], получим:
[ x 1 i + x 2 j + x 3 k, y 1 i + y 2 j + y 3 k ] =
= [ x 1 i, y 1 i + y 2 j + y 3 k ]+ [ x 2 j, y 1 i + y 2 j + y 3 k ]+ [ x 3 k, y 1 i + y 2 j + y 3 k ]=
= x 1 y 2 k + x 1 y 3 (- j)+ x 2 y 1(- k)+ x 2 y 3 i + x 3 y 1 j + x 3 y 2(- i)=
=(x 2 y 3 – x 3 y 2 , x 3 y 1 – x 1 y 3, x 1 y 2 – x 2 y 1) (см. Рис. 1.20).
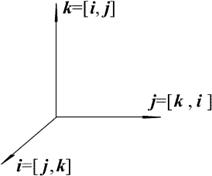
Рис. 1.20. Перемножение ортов осей
Для вычисления векторного произведения удобно использовать символический определитель:
[ x 1 i + x 2 j + x 3 k, y 1 i + y 2 j + y 3 k ] = 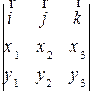 .
.
1.6. Преобразование координат
1.6.1.Преобразование поворота
Рассмотрим две системы декартовых координам с общим началом в точке O, полученные поворотом одна из другой на угол 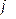 . Орты осей обозначим i, j встарой системе координам x, y и I, J в новой системе координат X, Y. Таким образом, для точки плоскости M будем иметь (см. рис. 1.21):
. Орты осей обозначим i, j встарой системе координам x, y и I, J в новой системе координат X, Y. Таким образом, для точки плоскости M будем иметь (см. рис. 1.21):
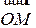 =x i + y j = X i + Y J
=x i + y j = X i + Y J
Рис. 1.21. Поворот осей
Slide_1_21 «Преобразование координат на плоскости (поворот)»
Выпишем соотношения между базисными векторами старой и новой координатных систем.
I =(I, i) i +(I, j) j = 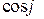 i +
i + 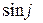 j, где (I, i)=
j, где (I, i)= 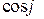 , (I, j)=
, (I, j)= 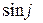 . Далее J = [[ I, j ], I ] = [[ I, j ],
. Далее J = [[ I, j ], I ] = [[ I, j ], 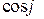 i +
i + 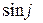 j ]=
j ]= 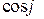 [[ I, j ], i ] +
[[ I, j ], i ] + 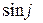 [[ I, j ], j ]=
[[ I, j ], j ]= 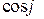 j +
j + 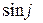 (- i). Таким образом, J = -
(- i). Таким образом, J = - 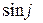 i +
i + 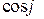 j.
j.
Обозначим, для краткости, a = 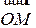 , тогда X=( a, I )=( a,
, тогда X=( a, I )=( a, 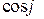 i +
i + 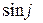 j )=
j )=
x 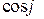 +y
+y 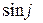 . Аналогично, Y=(a, J)=(a,
. Аналогично, Y=(a, J)=(a, 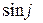 i +
i + 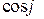 j)=
j)=
= - x 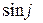 +y
+y 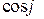 . Получены:
. Получены:
формулы преобразования координат при повороте осей на угол 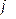 :
:
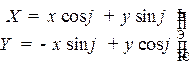 или
или 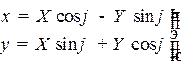
Пример. В уравнении второго порядка 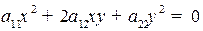 с помощью поворота системы координат избавиться от смешанного произведения xy.
с помощью поворота системы координат избавиться от смешанного произведения xy.
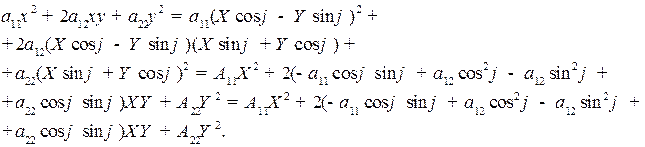 Коэффициент при
Коэффициент при 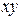 приравняем нулю:
приравняем нулю: 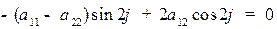 или
или  .
.
Равенство 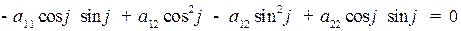 можно записать в другом виде. Обозначим через
можно записать в другом виде. Обозначим через 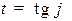 , тогда равенство
, тогда равенство 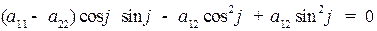 запишется в виде:
запишется в виде: 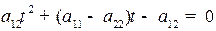 .
.
Выпишем выражения для коэффициентов 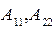 :
: 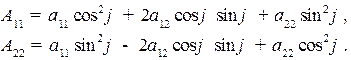
Отметим, что 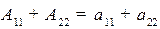 .
.
1.6.2.Преобразование сдвига
Рассмотрим две системы декартовых координам с общим началом в точке O, полученные сдвигом одна относительно другой. Орты осей обозначим i, j встарой системе координам x, y и I, J в новой системе координат X, Y. Таким образом, для точки плоскости M будем иметь (см. рис. 1.22):
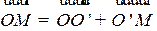 =x i + y j = X I + Y J
=x i + y j = X I + Y J
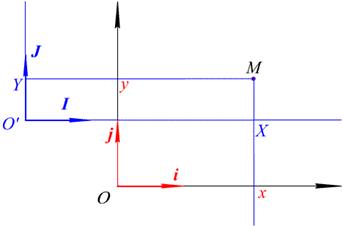
Рис. 1.22. Сдвиг осей
Slide_1_22 «Преобразование координат на плоскости»
Пусть координаты нового начала  равны:
равны: 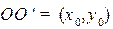 . Тогда
. Тогда 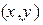 =
= 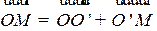 =
= 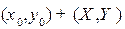 . Отсюда получаем соотношение между старыми и навыми координатами:
. Отсюда получаем соотношение между старыми и навыми координатами:
формулы преобразования координат при сдвиге
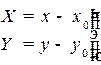
1.6.3. Полянные и сферические координаты
Положение точки на плоскости можно определять расстоянием r этой точки от начала координат и углом поворота радиус вектора точки 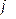 по отношению к горизонтальной оси x. Ось
по отношению к горизонтальной оси x. Ось 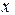 в этом случае называется полярной осью а пара чисел
в этом случае называется полярной осью а пара чисел 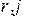 называется полярными координатами. Связь между декартовыми и полярными координатами выражается формулами:
называется полярными координатами. Связь между декартовыми и полярными координатами выражается формулами:
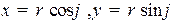 .
.
Slide_1_22_1 «Порярные координаты»
В пространстве положение точки можно определить тремя координатами (сферические координаты), которые связаны с декартовыми координатами формулами:
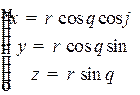 ,
,
где 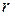 - расстояние от точки до начала координат,
- расстояние от точки до начала координат, 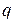 - угол между радиус вектором точки и плоскостью
- угол между радиус вектором точки и плоскостью 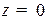 ,
, 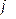 - полярный угол проекции точки на плоскость
- полярный угол проекции точки на плоскость 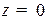 в системе координат
в системе координат 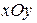 .
.
Slide_1_22_2 «Сферические координаты»
1.7. Смешанное произведение двух векторов, его свойства и выражение через координаты сомножителей
1.7.1. Определение.
Смешанным произведением трех векторов a, b, c назвается выражение
([ a, b ], с). Обозначается смешанное произведение (a, b, c).
(a, b, c) = ([ a, b ], с).
Из определения получаем:  (a, b, c)
(a, b, c)  =
=  [ a, b ]
[ a, b ] 
 с
с 
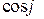 =
=  , где
, где  - площадь основания, а
- площадь основания, а  - высота параллелепипеда, построенного на векторах
- высота параллелепипеда, построенного на векторах
a, b, c. Модуль смешанного произведения  (a, b, c)
(a, b, c)  равен объему параллелепипеда, построенного на векторах a, b, c. (a, b, c) > 0, если тройка векторов – правая, (a, b, c) < 0, если тройка векторов – левая, (a, b, c) = 0, если тройка векторов компланарная (см. рис. 1.23).
равен объему параллелепипеда, построенного на векторах a, b, c. (a, b, c) > 0, если тройка векторов – правая, (a, b, c) < 0, если тройка векторов – левая, (a, b, c) = 0, если тройка векторов компланарная (см. рис. 1.23).
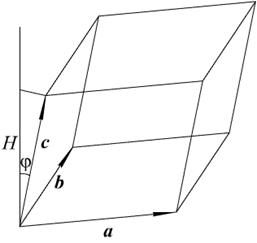
Рис. 1.23. Модуль смешанного произведения
Slide_1_23 «Геометрический смысл смешанного произведения»
Следствие. (a, b, c) = ([ a, b ], с) =(a, [ b, c ]).
Равенство нулю смешанного произведения означает компланарность векторов a, b, c.
1.7.2. Выражение смешанного произведения в декартовых координатах
Если x =x 1 i + x 2 j + x 3 k, y =y 1 i + y 2 j + y 3 k, z =z 1 i + z2 j + z 3 k, то
(x, y, z) = 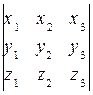 .
.
Доказательство:
(x, y, z) = ([ x, y ], z) = ((x 2 y 3 – x 3 y 2 , x 3 y 1 – x 1 y 3, x 1 y 2 – x 2 y 1), c) =
=(x 2 y 3 – x 3 y 2 ) z 1 +(x 3 y 1 – x 1 y 3) z2 + (x 1 y 2 – x 2 y 1) z3= 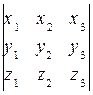 .
.
Slide_1_23_1 «Смешанное произведение»
Следствие. Необходимым и достаточным условием равенства нулю определителя
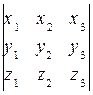 = 0, является компланарность векторов
= 0, является компланарность векторов
x = (x 1, x 2, x 3), y = (y 1, y 2, y 3), z = (z 1, z2, z 3).
Глава 2. Прямые и плоскости
2.1. Уравнение прямой на плоскости и плоскости в пространстве, ортогональных данному вектору и проходящих через данную точку
Выпишем уравнение прямой, проходящей через точку  , перпендикулярно заданному вектору N. Эта прямая может быть описана, как геометрическое место точек
, перпендикулярно заданному вектору N. Эта прямая может быть описана, как геометрическое место точек 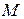 , для которых
, для которых 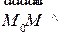 N:
N: 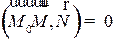 . Последнее соотношение, записанное в декартовых координатах, будет выглядеть следующим образом:
. Последнее соотношение, записанное в декартовых координатах, будет выглядеть следующим образом:
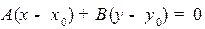 , (1)
, (1)
где N=  -нормаль,
-нормаль,  , M=
, M=  - текущая точка на прямой (см. рис. 2.1).
- текущая точка на прямой (см. рис. 2.1).
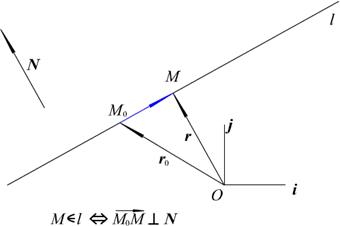
Рис. 2.1. Прямая на плоскости (общее уравнение)
Уравнение (1) называется общим уравнение прямой на плоскости. Уравнение (1) можно записать в векторном виде:
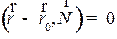 (1)
(1)
Отметим, что условием того, что уравнение (1) представляет уравнение прямой должно выполняться условие 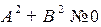 .
.
Аналогичные рассуждения можно провести и для плоскости в пространстве (см. рис. 2.2).
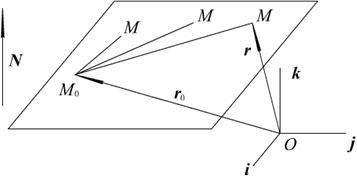
Рис. 2.2. Общее уравнение плоскости
Уравнение прямой, не проходящей через начало координат можно представить в виде (общее уравнение прямой 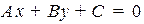 поделить на
поделить на 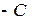 )
)
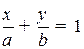 .
.
Это уравнение называется уравнением прямой в отрезка. Геометрически числа 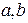 имеют смысл отрезков, отсекаемых прямой на соответствующих осях.
имеют смысл отрезков, отсекаемых прямой на соответствующих осях.
Slide_2_2_1 «Уравнение прямой в отрезках»
Уравнение плоскости, проходящей через точку 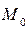 , перпендикулярно заданному вектору N, представляет собой геометрическое место точек
, перпендикулярно заданному вектору N, представляет собой геометрическое место точек 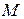 , для которых
, для которых 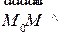 N:
N:  . Последнее соотношение, записанное в декартовых координатах, будет выглядеть следующим образом:
. Последнее соотношение, записанное в декартовых координатах, будет выглядеть следующим образом:
 , (2)
, (2)
где N= 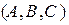 -нормаль,
-нормаль, 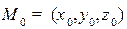 , M=
, M= 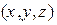 . Или в векторном виде
. Или в векторном виде
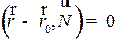 (2)
(2)
Уравнения (2) называются общим уравнение плоскости в пространстве. Для краткости, в этом случае, будем говорить, что задана плоскость 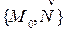 .
.
2.2. Общее уравнение первого порядка на плоскости и в пространстве, его исследование
2.2.1.Общее уравнение первого порядка на плоскости.
Рассмотрим общее уравнение первого порядка:
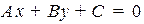 .
.
Если 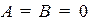 , то при
, то при 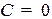 это уравнение определяет всю плоскость (решением уравнения является любая точка
это уравнение определяет всю плоскость (решением уравнения является любая точка 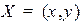 на плоскости).
на плоскости).
При 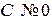 уравнение не имеет решений и определяет, таким образом, пустое множество.
уравнение не имеет решений и определяет, таким образом, пустое множество.
Если 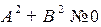 , то уравнение имеет бесконечно много решений. Геометрически это множество является прямой на плоскости, перпендикулярной вектору
, то уравнение имеет бесконечно много решений. Геометрически это множество является прямой на плоскости, перпендикулярной вектору 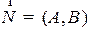 . Действительно, пусть
. Действительно, пусть  некоторое решение уравнения
некоторое решение уравнения 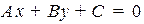 :
: 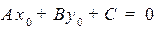 . Тогда для любого решения
. Тогда для любого решения 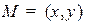 этого уравнения будет справедливо равенство:
этого уравнения будет справедливо равенство: 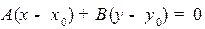 , которое задает прямую на плоскости.
, которое задает прямую на плоскости.
Slide_2_3_0 «Общее уравнении прямой на плоскости»
Отметим одно важное свойство общего уравнения прямой.
Отложим вектор нормали 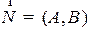 из какой нибудь точки прямой, заданной уравнением
из какой нибудь точки прямой, заданной уравнением 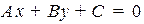 . Пусть
. Пусть 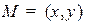 какая либо точка плоскости, тогда
какая либо точка плоскости, тогда
1) если 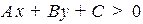 , то точка
, то точка 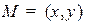 лежит с той же стороны от прямой, что и вершина вектора
лежит с той же стороны от прямой, что и вершина вектора 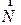 ,
,
2) если 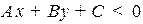 , то точка
, то точка 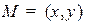 и вершина
и вершина 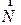 лежат с разных сторон от прямой,
лежат с разных сторон от прямой,
3) если 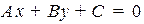 , то точка
, то точка  принадлежит прямой (см. рис. 2.3.).
принадлежит прямой (см. рис. 2.3.).
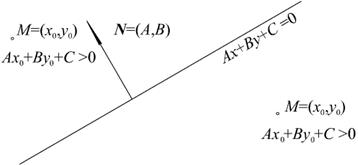
Рис. 2.3. Расположение точек относительно прямой
Докажем это утверждение. Пусть  точка прямой
точка прямой 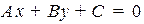 , тогда
, тогда 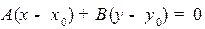 и
и 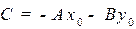 . Если вектор
. Если вектор 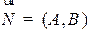 отложен от прямой, например, из точки
отложен от прямой, например, из точки 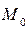 , то условие того, что точка
, то условие того, что точка 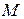 лежит в той же стороны от прямой, что и вершина вектора
лежит в той же стороны от прямой, что и вершина вектора 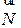 можно записать в виде
можно записать в виде 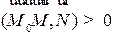 . Обозначим этот случай а). Если с другой стороны, то
. Обозначим этот случай а). Если с другой стороны, то 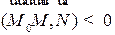 . Обозначим этот случай b). Или в развернутом виде:
. Обозначим этот случай b). Или в развернутом виде: 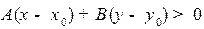 в случае а) и
в случае а) и 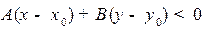 в случае b). Итак, в первом случае
в случае b). Итак, в первом случае 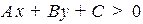 , а во втором
, а во втором 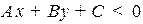 (см. рис. 2.4).
(см. рис. 2.4).
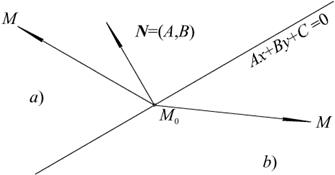
Рис. 2.4. Разное расположение точек относительно прямой
2.2.2.Общее уравнение первого порядка в пространстве
Рассмотрим общее уравнение первого порядка в пространстве:
 .
.
Если 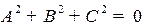 , то это, либо все пространство (
, то это, либо все пространство (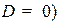 , либо пустое множества (
, либо пустое множества (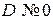 ).
).
Если 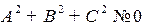 , то это уравнение определяет плоскость с вектором нормали
, то это уравнение определяет плоскость с вектором нормали 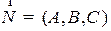 .
.
Проверяется так же, как и для прямой на плоскости. Важное свойство общего уравнения плоскости в пространстве.
Отложим вектор нормали 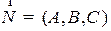 из какой нибудь точки плоскости, заданной уравнением
из какой нибудь точки плоскости, заданной уравнением  . Пусть
. Пусть 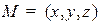 какая либо точка пространства, тогда
какая либо точка пространства, тогда
1) если 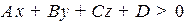 , то точка
, то точка 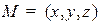 лежит с той же стороны от прямой, что и вершина вектора
лежит с той же стороны от прямой, что и вершина вектора  ,
,
2) если 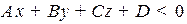 , то точка
, то точка 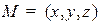 и вершина
и вершина 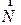 лежат с разных сторон от прямой,
лежат с разных сторон от прямой,
3) если  , то точка
, то точка  принадлежит плоскости (см. рис. 2.5).
принадлежит плоскости (см. рис. 2.5).
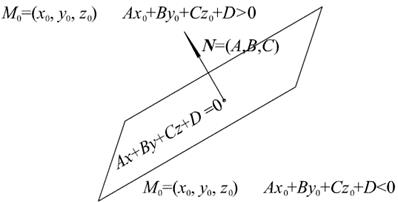
Рис. 2.5. Расположение точек относительно плоскости
Проверяется так же, как и для прямой на плоскости.
2.3. Нормальное уравнение прямой на плоскости и плоскости в пространстве. Приведение общего уравнения первого порядка к нормальному виду
2.3.1.Нормальное уравнение прямой на плоскости.
Рассмотрим общее уравнение прямой на плоскости.
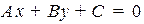 ,
, 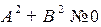 (1)
(1)
Определение. В случае 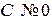 нормальным уравнением прямой (1) называется уравнение
нормальным уравнением прямой (1) называется уравнение
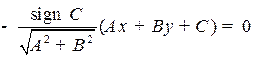 .
.
Это уравнение можно записать в виде: 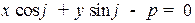 (см. рис. 2.6)
(см. рис. 2.6)

Рис. 2.6. Нормальное (нормированное) уравнение прямой
Slide_2_6 «Нормальное уравнение прямой»
n = 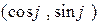 – единичный вектор нормали, ориентированный так, что будучи отложенным из начала координат, он будут «смотреть» в сторону прямой.
– единичный вектор нормали, ориентированный так, что будучи отложенным из начала координат, он будут «смотреть» в сторону прямой.
Slide_2_6_1 «Нормировка уравнения прямой»
Пример. Пронормировать уравнение прямой 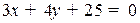 .
.
Модуль вектора нормали (3, 4) равен 5. Делим уравнение прямой на 5 и берем знак противоположный знаку свободного коеффициента 25, получим нормальное уравнение прямой: 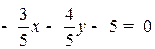 .
.
С помощью нормального уравнения прямой определяют расстояние от точек до прямых, именно:
Расстояние от точки 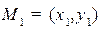 до прямой
до прямой 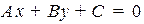 с нормальным уравнением
с нормальным уравнением 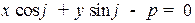 равно
равно
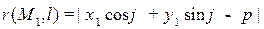 .
.
Slide_2_6_2 «Расстояние от точки до прямой»
Пример. Найти расстояние от точки 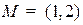 до прямой
до прямой 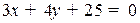 (l).
(l).
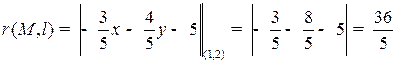 .
.
2.3.2. Нормальное уравнение плоскости в пространстве
Рассмотрим общее уравнение плоскости в пространстве
 ,
, 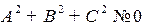 (1)
(1)
Определение. В случае 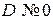 нормальным уравнением плоскости (1) называется уравнение
нормальным уравнением плоскости (1) называется уравнение
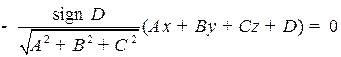 .
.
Это уравнение можно записать в виде: 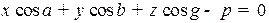 (см. рис. 2.7)
(см. рис. 2.7)
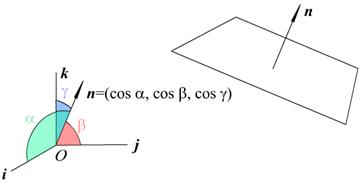
Рис. 2.7. Нормальное уравнение плоскости (через направляющие косинусы нормали)
n = 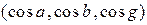 – единичный вектор нормали, ориентированный так, что будучи отложенным из начала координат, он будут «смотреть» в сторону плоскости.
– единичный вектор нормали, ориентированный так, что будучи отложенным из начала координат, он будут «смотреть» в сторону плоскости.
Пример. Пронормировать уравнение прямой 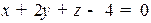 .
.
Модуль вектора нормали (1, 2, 1) равен 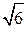 . Делим уравнение прямой на
. Делим уравнение прямой на 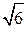 и берем знак противоположный знаку свободного коеффициента -4, получим нормальное уравнение прямой:
и берем знак противоположный знаку свободного коеффициента -4, получим нормальное уравнение прямой: 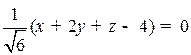 .
.
С помощью нормального уравнения плоскости определяют расстояние от точек до плоскостей, именно:
Расстояние от точки 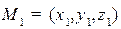 до плоскости
до плоскости 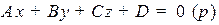 с нормальным уравнением
с нормальным уравнением 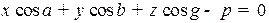 равно
равно
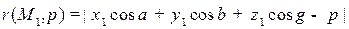 .
.
Пример. Найти расстояние от точки 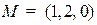 до плоскости
до плоскости 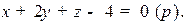
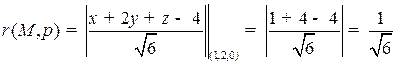 .
.
2.4. Различные формы уравнения прямой на плоскости и в пространстве. Переход от одной формы к другой
2.4.1.Общее уравнение прямой на плоскости
Ранее уже рассматривалось уравнение прямой: 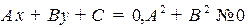 , В векторной виде:
, В векторной виде: 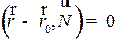 .
.
2.4.2.Параметрическое уравнение прямой на плоскости
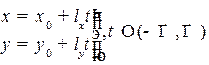 , В векторном виде: r = r0 + l
, В векторном виде: r = r0 + l 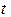 ,
, 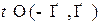 .
.
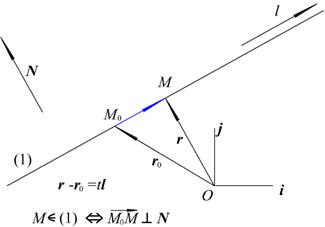
Рис. 2.8. Параметрическое уравнение прямой
Slide_2_8 «Параметрическое уравнение прямой на плоскости»
Вектор l называется направляющим вектором прямой (см. рис. 2.8).
2.4.3.Каноническое уравнение прямой на плоскости
Каноническое уравнение, в действительности, является несколько другой записью параметрического уравнения:
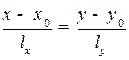 .
.
Для канонического уравнения прямой, так же как и для параметрического уравнения, нужна точка на прямой и направляющий вектор. Для краткости, в этом случае, будем говорить, что задана прямая 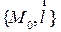 .
.
Slide_10_1 «Каноническое уравнение прямой на плоскости»
2.4.4. Переход от одной формы уравнения прямой к другой на плоскости
Не тривиальным является только переход от общего к уравнения к параметрическому и обратно.
От общего к параметрическому.
Общее уравнение определяется нормалью N и точко  на прямой. Если точка не задана, то ее можно найти, задав
на прямой. Если точка не задана, то ее можно найти, задав 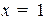 (в случае
(в случае 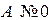 ) или
) или 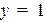 (в случае
(в случае  ) и решив уравнение
) и решив уравнение 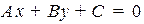 относительно оставшейся неизвестной. Например, для уравнения
относительно оставшейся неизвестной. Например, для уравнения 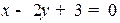 полагаем
полагаем 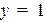 и находим
и находим 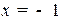 ,
, 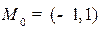 . После того, как точка
. После того, как точка 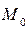 найдена находим направляющий вектор прямой l. В качестве направляющего вектора берется любой вектор, ортогональный вектору нормали N. Для уравнения
найдена находим направляющий вектор прямой l. В качестве направляющего вектора берется любой вектор, ортогональный вектору нормали N. Для уравнения 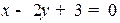 таким вектором может служить вектор l=
таким вектором может служить вектор l= 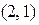 . В параметрическом виде уравнение будет выглядеть следующим образом:
. В параметрическом виде уравнение будет выглядеть следующим образом:
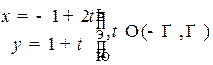 , в каноническом:
, в каноническом: 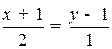 .
.
От параметрического к общему.
Для обратного перехода дроби 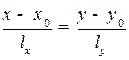 формально преобразуются у виду:
формально преобразуются у виду: 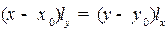 и далее получаем общее уравнение прямой:
и далее получаем общее уравнение прямой: 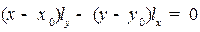 .
.
Пример. Привести к общему виду уравнение 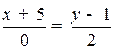 . После указанных преобразований получим:
. После указанных преобразований получим: 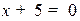 .
.
2.4.5.Уравнение прямой в пространстве, как пересечение двух плоскостей
Прямую в пространстве можно задать, указав две плоскости, линией пересечения которых, является данная прямая. При этом используют следующую запись:
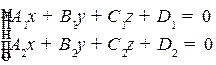
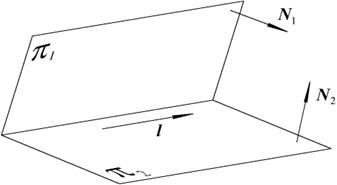
Рис. 2.9. Прямая, как пересечение двух плоскостей
Для того, чтобы указанные плоскости определяли прямую, они должны быть не параллельны, то есть вектора 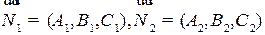 не должны быть коллениарны (см. рис. 2.9).
не должны быть коллениарны (см. рис. 2.9).
2.4.6.Параметрическое уравнение прямой в пространстве
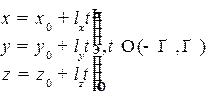 , в векторном виде: r = r0 + l
, в векторном виде: r = r0 + l  ,
, 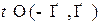 , (см. рис. 2.10).
, (см. рис. 2.10).
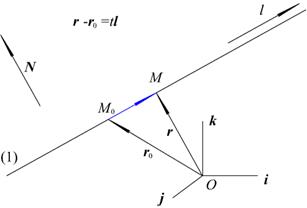
Рис. 2.10. Парметрическое уравнение прямой
2.4.7.Каноническое уравнение прямой в пространстве
Каноническое уравнение, в действительности, является несколько другой записью параметрического уравнения:
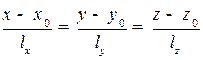 .
.
Для канонического уравнения прямой, так же как и для параметрического уравнения, нужна точка на прямой и направляющий вектор. Для краткости, в этом случае, будем говорить, что задана прямая 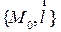 .
.
Slide_10_2 «Каноническое уравнение прямой в пространстве»
2.4.8. Переход от одной формы уравнения прямой к другой в пространстве
От общего к параметрическому
Задав какое нибудь значение одной из переменных  , и решая систему
, и решая систему
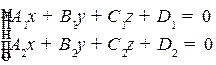 относительно оставшихся переменных можно будет найти какую нибудь точку
относительно оставшихся переменных можно будет найти какую нибудь точку 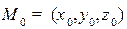 на прямой. Направляющий вектор можно найти, как векторное произведение нормалей плоскостей, определяющих данную прямую: l = [ N1, N2 ].
на прямой. Направляющий вектор можно найти, как векторное произведение нормалей плоскостей, определяющих данную прямую: l = [ N1, N2 ].
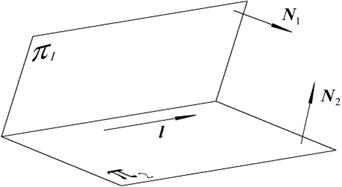
Рис. 2.11. Переход от одного уравнения к другому
От параметрического к общему
Из дробей 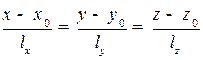 формально выписываем два равенства:
формально выписываем два равенства: 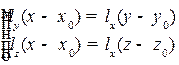 , которые и дадут две плоскости, определяющие данную прямую (см. рис. 2.11).
, которые и дадут две плоскости, определяющие данную прямую (см. рис. 2.11).
2.4.9. Угол между двумя прямыми на плоскости и в простанстве, между двумя плолоскостями в пространстве, между прямой и плоскостью
Угол между двумя прямыми на плоскости равен углу между их нормалями. Угол между двумя прямыми в пространстве равен углу между их направляющими векторами. Угол между двумя плоскостями определяется, как угол между их нормалями. Угол между прямой и плоскостью в пространстве определяется, как угол между направляющим вектором прямой и нормалью к плоскости.
2.5. Барицентрические координаты. Деление отрезка в данном соотношении. Пучок прямых. Пучок плоскостей.
Положение точки 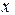 на отрезке
на отрезке 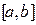 можно задать величиной
можно задать величиной 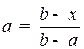 , показывающей в каком соотношении точка
, показывающей в каком соотношении точка 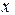 делит отрезок. Величина
делит отрезок. Величина 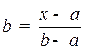 также определяет положение точки
также определяет положение точки 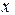 . Числа
. Числа 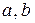 , однозначно определяющие положение точки на отрезке, называются барицентрическими координатами точки
, однозначно определяющие положение точки на отрезке, называются барицентрическими координатами точки 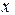 . Отметим следующие свойства барицентрических координат:
. Отметим следующие свойства барицентрических координат:
1. 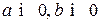 .
.
2. 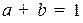 .
.
3. 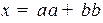 .
.
Середина отрезка имеет координаты: 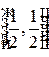 .
.
Рассмотрим три точки на плоскости или в пространстве: 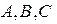 . Любая точка
. Любая точка 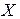 треугольника
треугольника 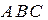 однозначно определятся тремя барицентрическими координатами:
однозначно определятся тремя барицентрическими координатами: 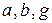 , обладающими следующими свойствами:
, обладающими следующими свойствами:
1. 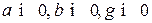 .
.
2. 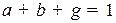 .
.
3. 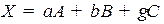 .
.
Линейные операции сложения и умножения на числа над точками определяются так же, как и над векторами. Например, третье условие можно записать в виде: 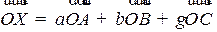 .
.
Геометрически числа 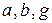 определяются отношениями площадей треугольников
определяются отношениями площадей треугольников 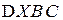 ,
, 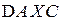 ,
, 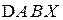 ко всей прощади треугольника
ко всей прощади треугольника 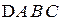 (см. рис. 2.12).
(см. рис. 2.12).
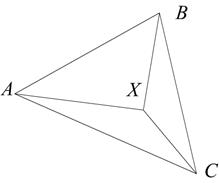
Рис. 2.12. Барицентрические координаты
Если в вершины треугольника поместить одинаковые массы, то центр тяжести такой системы будет иметь барицентрические координаты 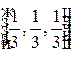 .
.
Так же как для треугольника вводятся барицентрические координаты для тетраэдра 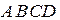 (не обязательно правильного). Положение внутренней точки
(не обязательно правильного). Положение внутренней точки 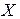 тетраэдра однозначно определяется четырьмя числами
тетраэдра однозначно определяется четырьмя числами 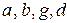 , удовлетворяющими следующим свойствам:
, удовлетворяющими следующим свойствам:
1. 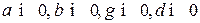 .
.
2. 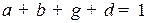 .
.
3. 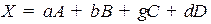 .
.
Геометрически барицентрические координаты равны отношениям объемов внутренних тетраэдров 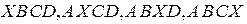 к объему тетраэдра
к объему тетраэдра 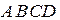 (см. рис. 2.13).
(см. рис. 2.13).
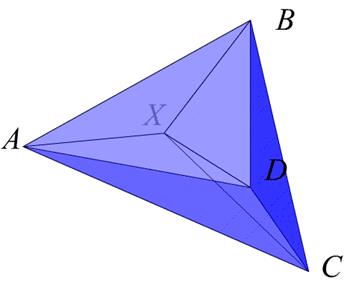
Рис. 2.13. Смысл барицентрических координат
Если в вершины тетраэдра поместить одинаковые массы, то центр тяжести такой системы будет иметь барицентрические координаты 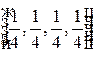 .
.
Свойство 2 барицентрических координат называют еще разбиением единицы.
С помощью барицентрических координат описывают положение прямых и плоскостей в пучках. Вначале дадим определение пучка прямых.
Рассмотрим точку, определяемую двумя не параллельными прямыми:
 .
.
Множество всех прямых, проходящих через эту точку назывется пучком прямых. Между множеством всех прямых пучка и множеством разбиения единицы 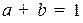 имеется взаимно однозначное соответствие, именно, любая прямая из пучка
имеется взаимно однозначное соответствие, именно, любая прямая из пучка
| <== предыдущая лекция | | | следующая лекция ==> |
| | | Иванова Любовь Павловна |