Классификация алгоритмов

Различают линейные, разветвляющие и циклические алгоритмы.

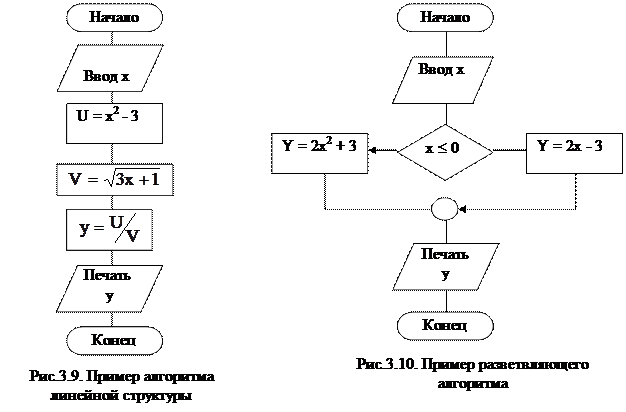
В алгоритме линейной структуры предписания алгоритма выполняются последовательно друг за другом в естественном порядке. В качестве примера приведем алгоритм вычисления Y по формуле (рис.3.9):

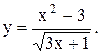
В разветвляющемся алгоритме направление решения задачи может изменяться в зависимости от результатов проверки некоторого логического условия. Выполнение алгоритма производится по нескольким ветвям, объединяющим некоторым образом группы операций. В каждом конкретном случае, в зависимости от проверки условия, процесс реализуется только по одной ветви.

В качестве примера составим алгоритм (рис.3.10) определения значения переменной Y в соответствии с заданием:

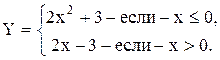
При описании разветвляющихся алгоритмов используется понятие условного и безусловного переходов.

Предписание безусловного перехода имеет вид: m: идти к n, где m, n - номера некоторых предписаний. В этом случае после предписания с номером m выполняется предписание не (m+1), а n.

Предписание условного перехода выглядит так: m: если р, идти к n, иначе к k, где m, n, k - номера некоторых предписаний; p - проверка условия. Если p выполняется (p - истинно), то после проверки условия реализуется предписание с номером n, если условие не выполняется (p - ложно), то реализуется предписание с номером k.

Характерной особенностью большинства используемых на практике алгоритмов является их цикличность, т.е. неоднократное выполнение отдельных частей. Повторяющийся участок называется циклом. Алгоритмы, содержащие циклы, называются циклическими. Цикл выполняется при последовательных значениях по крайней мере одного параметра, который называется параметром цикла. В зависимости от значения параметра цикла возможны два действия: выполнение операции цикла, выход из цикла.

По способу определения числа повторений цикла выделяются два вида цикла:

Арифметический, в котором осуществляется заранее известное число раз повторений цикла. В данном случае задаются: начальное и конечное значение параметра цикла, закон изменения параметра цикла при каждом его повторении. Для подсчета числа повторений цикла выделяется переменная, которая принимает целочисленные значения и именуется счетчиком. По способу управления числом повторений счетчик подразделяется на прямой и обратный, т.е. при каждом прохождении цикла в первом случае осуществляется увеличение счетчика, в другом - уменьшение. Характерными примерами арифметических циклов являются вычисление конечной суммы, которая сводится к нахождению суммы заданного количества слагаемых, или табулирование некоторой функции, которая сводится к вычислению некоторой функции при изменении аргумента в заданных пределах и с заданным шагом.

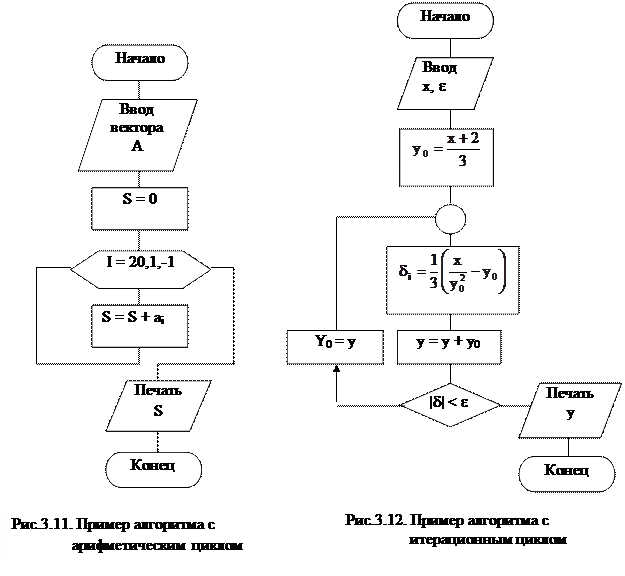
Пример: составить алгоритм суммирования элементов вектора А = (a₁, а₂…а₂₀) по формуле:

Вычисления выполняются следующим образом: на каждом прохождении цикла номер слагаемого i увеличивается на единицу i = i + 1, а сумма изменяется на величину i-ого слагаемого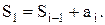

Цикл повторяется до тех пор, пока не будут проссумированы все n слагаемых. Алгоритм приведен на рис.3.11.

Итерационный цикл - число повторений которого заранее неизвестно и не может быть вычислено. В итерационных циклах реализуется метод последовательных приближений. Выход из цикла осуществляется при выполнении некоторого условия, связанного с проверкой значения монотонно изменяющейся величины. Она характеризует точность, достигаемую на очередном шаге итерационного процесса. Типичная задача итерационного цикла - нахождение корня алгебраического уравнения: f(x) = 0 методом итераций на заданном отрезке изменения аргумента {x_а, х_b}. Представим уравнение в таком виде:

x = j(x).

Очередное приближение корня равно значению функции j от приближения корня, полученного на предыдущем шаге итерации

x_i = j(x_i-1).

Если существует предел последовательности значений x_i, то сушествует корень x_n. Вычисления продолжаются до тех пор, пока абсолютное значение погрешности вычисления (разность значений корня двух соседних итераций) станет меньше некоторого малого числа e:

|x_i – x_i-1|< e.

Алгоритм реализуется следующим образом. Вначале находят текущую погрешность вычислений по формуле: d_i = x_i – x_i-1 = j(x_i-1) – x_i-1. А затем определяют значение нового приближения корня: x_i = x_i-1 + d_i.

В качестве примера составим алгоритм вычисления корня кубического:

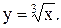
В результате элементарных преобразований (возведение в куб, прибавление к левой части 2y³, прибавление к правой части 2y³ + y³ - y³, деление на 3y²) получим формулу:

Принимая значения y в правой части за предыдущее приближение корня, а в левой части за последующее, получим итерационную формулу:

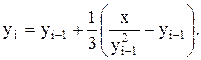
Погрешность вычисляется по формуле:

За начальное приближение корня принимаем величину:

y₀ = (x + 2)/3.

Блок-схема алгоритма вычисления корня кубического изображена на рис.3.12.

Существуют сложные циклы. Любой цикл, включающий один или несколько других циклов называется сложным. Охватывающий цикл принято называть внешним, а входящий во внешний цикл внутренним.

Пример: Составить блок-схему алгоритма суммирования элементов таблицы, состоящей из 6 столбцов и 5 строк

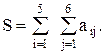
Блок-схема алгоритма сложного цикла изображена на рис.3.13.