
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Многогранники
|
|
На комплексном чертеже многогранники изображаются проекциями своих вершин и ребер с учетом видимости.
Задача. Построить проекции многогранника по заданным вершинам. Найти недостающие проекции точки М, принадлежащей поверхности многогранника (рис.55).
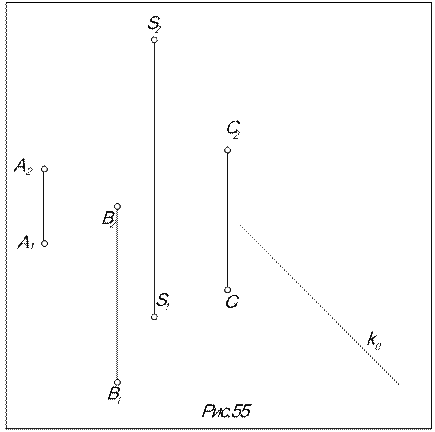 Алгоритм решения
Алгоритм решения
1.Построив профильные проекции вершин пирамиды, соединяем одноименные проекции вершин отрезками и получаем проекции пирамиды. Видимость ребер и граней определяем по представлению. На П1 видны боковые ребра и грани пирамиды, т.к. вершина S располагается над основанием АВС. Рассматривая горизонтальную проекцию совместно с направлением на П2, определяем, что видимыми на П2 являются грани ASB и BSС, а грань АSC и её ребро АС – невидимы. Аналогичным образом определяем, что на П3 невидимыми являются ребра прилегающие к вершине С.
 2. Строим недостающие проекции точки М, принадлежащей пирамиде, используя признак принадлежности точки гранной поверхности: точка принадлежит поверхности многогранника, если лежит на прямой, принадлежащей какой-либо грани этой поверхности. Точка М видима на П2 (её проекция не заключена в скобки), следовательно, она лежит в грани ASB. Проводим в этой грани через М2 произвольную прямую, например, S212 , строим остальные проекции прямой и по принадлежности им находим недостающие проекции точки. Т.к. грань ASB видима на всех проекциях, то и точка М везде является видимой.
2. Строим недостающие проекции точки М, принадлежащей пирамиде, используя признак принадлежности точки гранной поверхности: точка принадлежит поверхности многогранника, если лежит на прямой, принадлежащей какой-либо грани этой поверхности. Точка М видима на П2 (её проекция не заключена в скобки), следовательно, она лежит в грани ASB. Проводим в этой грани через М2 произвольную прямую, например, S212 , строим остальные проекции прямой и по принадлежности им находим недостающие проекции точки. Т.к. грань ASB видима на всех проекциях, то и точка М везде является видимой.
7.1.Пересечение многогранника плоскостью
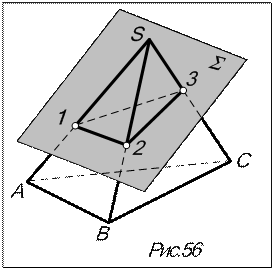
При пересечении многогранника плоскостью получают многоугольник, вершины которого - точки пересечения ребер многогранника с секущей плоскостью, а стороны - линии пересечения его граней с той же плоскостью (рис.56).
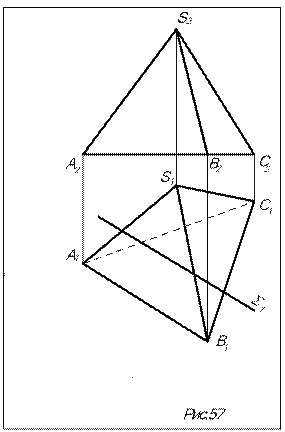 Задача. Построить проекции и НВ сечения пирамиды SАВС плоскостью S (S1) (рис.57).
Задача. Построить проекции и НВ сечения пирамиды SАВС плоскостью S (S1) (рис.57).
Алгоритм решения
1.Так как S - горизонтально проецирующая плоскость, то отрезок ее вырожденной проекции S1, лежащий внутри очерка пирамиды, - горизонтальная проекция сечения. Вершины сечения сначала находим на П1, как результат пересечения S1 с проекциями ребер, а затем на П2 - по принадлежности ребрам.
2. Найденные одноименные проекции вершин сечения соединяем отрезками, руководствуясь правилом: отрезками прямых можно соединять только точки, лежащие в одной грани многогранника.
3. НВ сечения определяем способом замены плоскостей проекций:
П2  П4
П4  S, П1 / П2 (x12)
S, П1 / П2 (x12) 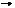 П1 / П4 (s14
П1 / П4 (s14  S1)
S1)
 4. Видимость на чертеже определяем по представлению. Из двух скрещивающихся ребер SB и АС при взгляде сверху ближе к наблюдателю SB, поэтому АС на П1 невидимо. На П2 невидимой является грань ASC и лежащая в ней сторона сечения (12).
4. Видимость на чертеже определяем по представлению. Из двух скрещивающихся ребер SB и АС при взгляде сверху ближе к наблюдателю SB, поэтому АС на П1 невидимо. На П2 невидимой является грань ASC и лежащая в ней сторона сечения (12).
Задача. Построить сечение призмы ABC плоскостью D(m  n) общего положения (рис.58).
n) общего положения (рис.58).
Алгоритм решения
1. Т.к. боковые грани и ребра призмы – горизонтально проецирующие, то горизонтальная проекция сечения DEF совпадает с горизонтальным очерком призмы, а горизонтальные проекции вершин - с горизонтальными проекциями боковых ребер: D1= A1, E1= B1, F1= C1.
2. На остальных плоскостях проекций вершины находим по принадлежности их секущей плоскости D(m  n), проводя в ней прямые, проходящие через горизонтальные проекции вершин. Например, для нахождения фронтальных проекций вершин D и E продолжаем сторону сечения D1Е1 до пересечения с проекцией прямой m1(D1Е1
n), проводя в ней прямые, проходящие через горизонтальные проекции вершин. Например, для нахождения фронтальных проекций вершин D и E продолжаем сторону сечения D1Е1 до пересечения с проекцией прямой m1(D1Е1  m1=11 ), находим 12
m1=11 ), находим 12 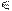 m2 и проводим через неё прямую, параллельную n2, т.к. судя по горизонтальной проекции, n
m2 и проводим через неё прямую, параллельную n2, т.к. судя по горизонтальной проекции, n  DE. На пересечении этой прямой с ребрами А и В и расположены проекции вершин D2 и E2 Вершину F находим с помощью прямой 23.
DE. На пересечении этой прямой с ребрами А и В и расположены проекции вершин D2 и E2 Вершину F находим с помощью прямой 23.
3. Видимость на П2 определяем по представлению. При взгляде на П2 прямая m располагается за призмой и часть её, лежащая внутри очерка призмы, будет на П2 невидима. Соответственно, верхние части боковых ребер А, В и С будут видны вплоть пересечения их с плоскостью D (m  n) в точках D, E, F. Невидимой на П2 будет и грань АС призмы и лежащая в ней сторона сечения DF.
n) в точках D, E, F. Невидимой на П2 будет и грань АС призмы и лежащая в ней сторона сечения DF.
 Задача. Построить проекции сечения наклонной призмы плоскостью q (m
Задача. Построить проекции сечения наклонной призмы плоскостью q (m 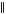 n) (рис.59).
n) (рис.59).
Алгоритм решения
Т.к. секущая плоскость, грани и ребра призмы - общего положения, то вершины сечения находим по алгоритму решения первой основ-ной позиционной задачи: а) заключаем ребра призмы в проецирующие плоскости; б) находим линии пересечения заданной и вспомогательных плоскостей; в) находим точки пересечения ребер с соответствующими построенными линиями пересечения.
1. Для нахождения точки пересечения ребра А с плоскостью q заключаем ребро во фронтально проецирующую плоскость S (S2= l2). Находим на П1 линию l пересечения S с заданной плоскостью q по двум точкам 1 и 2 пересечения S с прямыми m и n плоскости q:
1=S 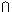 m, 2=S
m, 2=S 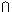 n, 1
n, 1 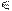 l
l 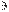 2.
2.
Находим точку D пересечения построенной линии пересечения l с ребром А:
D1 = А1  l1, D2
l1, D2 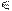 А2.
А2.
2. По аналогичному алгоритму с помощью фронтально проецирующих плоскостей D(D2) и L (L 2) находим точки Е и F пересечения ребер В и С с секущей плоскостью q. При этом, т.к. вспомогательные секущие плоскости S, D и L параллельны, то они пересекают призму по параллельным прямым. Поэтому для построения горизонтальных проекций прямых р1 и к1 достаточно построить на П1 по одной точке им, им принадлежащей (31 и 41 ).
3. Остальные ребра призмы плоскостью q не пересекаются, таким образом, сечение призмы представляет собой треугольник D, Е, F. Соединяем одноименные проекции построенных вершин и получаем проекции сечения.
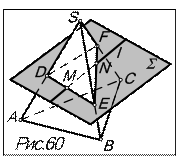 4. Видимость элементов чертежа определяем по представлению. Для определения видимости на П2 рассматриваем горизонтальную проекцию совместно со стрелкой – направлением взгляда на П2 . Прямая m располагается за призмой и ее часть, расположенная внутри очерка призмы невидима. Следовательно, участки боковых ребер, расположенные выше точек D, Е, F будут видны на П2. Все остальные участки ребер призмы, а также грань АВ и сторона сечения DF, в ней расположенная, на П2 невидимы. При взгляде сверху видимыми будут участки ребер призмы, расположенные выше секущей плоскости q (на П1 это участки боковых ребер, расположенные правее точек D1, Е1, F1), а также стороны сечения DЕ и DF, расположенные на видимых сверху гранях АВ и АС. Сторона ЕF, расположенная в невидимой сверху грани ВС, будет невидима.
4. Видимость элементов чертежа определяем по представлению. Для определения видимости на П2 рассматриваем горизонтальную проекцию совместно со стрелкой – направлением взгляда на П2 . Прямая m располагается за призмой и ее часть, расположенная внутри очерка призмы невидима. Следовательно, участки боковых ребер, расположенные выше точек D, Е, F будут видны на П2. Все остальные участки ребер призмы, а также грань АВ и сторона сечения DF, в ней расположенная, на П2 невидимы. При взгляде сверху видимыми будут участки ребер призмы, расположенные выше секущей плоскости q (на П1 это участки боковых ребер, расположенные правее точек D1, Е1, F1), а также стороны сечения DЕ и DF, расположенные на видимых сверху гранях АВ и АС. Сторона ЕF, расположенная в невидимой сверху грани ВС, будет невидима.
7.2.Пересечение многогранника прямой
Алгоритм решения (рис.60)
1. Через прямую проводим вспомогательную секущую плоскость: lÌ S.
2. Строим сечение многогранника плоскостью: DEF = Фмн 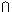 S.
S.
3. Определяем точки пересечения прямой с построенным сечением: M, N = l 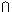 D DEF.
D DEF.
Задача. Найти точки пересечения прямой l с пирамидой SАВС (рис.61).
Алгоритм решения приведен выше:
 1. lÌ S Þ. l2 = S 2.
1. lÌ S Þ. l2 = S 2.
2. DEF = Фмн 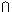 S Þ D2 = S2
S Þ D2 = S2 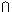 A2 S2, D1
A2 S2, D1 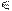 A1S1
A1S1
E2 = S2 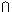 B2S2, E1
B2S2, E1 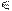 B1S1
B1S1
F2 = S2 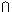 С2S2, F1
С2S2, F1 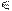 C1S1.
C1S1.
3. M, N = l 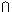 D DEF Þ M1 = l1
D DEF Þ M1 = l1 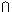 D1E1 , M2
D1E1 , M2 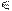 l2
l2
N1 = l1 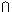 F1E1 , N2
F1E1 , N2 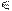 l2 .
l2 .
Видимость определяем по представлению. Грани АSB и BSC видимы на обеих проекциях, значит, видимы и точки M и N, в них лежащие и прилегающие к точкам участки прямой l. Невидимым является только участок прямой, лежащий внутри пирамиды. На П1 невидимым будет ребро АС пирамиды: скрещивающееся и конкурирующее с ним в видимости ребро SB расположено ближе к наблюдателю.
7.3.Взаимное пересечение многогранников
Линией пересечения двух многогранников является пространственная замкнутая ломаная, вершины которой - точки пересечения ребер одного многогранника с гранями второго и ребер второго с гранями первого, а сторонами - линии взаимного пересечения граней многогранников.
 При взаимном пересечении двух многогранников могут встретиться два случая: врезка и проницание. Врезкой называется случай, когда ни одна из поверхностей не пересекает другую полностью (рис.62а). Проницанием называется случай, когда одна из поверхностей полностью пересекается другой поверхностью (рис.62б). В случае врезки линия пересечения состоит из одной ломаной, а в случае проницания - из двух.
При взаимном пересечении двух многогранников могут встретиться два случая: врезка и проницание. Врезкой называется случай, когда ни одна из поверхностей не пересекает другую полностью (рис.62а). Проницанием называется случай, когда одна из поверхностей полностью пересекается другой поверхностью (рис.62б). В случае врезки линия пересечения состоит из одной ломаной, а в случае проницания - из двух.
Задача. Построить проекции линии пересечения пирамиды с поверхностью призматического отверстия (рис.63). 
Алгоритм решения
1. Т.к. поверхность призматического отверстия полностью пересекается поверхностью пирамиды (случай проницания), то линия пересечения (ЛП) состоит их двух пространственных замкнутых ломаных. Боковые грани призмы - фронтально проецирующие, поэтому фронтальная проекция ЛП совпадает с фронтальной проекции призматического отверстия, при этом проекции обеих фронтально конкурирующих контуров ЛП совпадают.
2. Находим вершины ломаной - точки пересечения ребер призмы с поверхностью пирамиды. Т.к. ребра призмы фронтально проецирующие, точки пересечения их с поверхностью пирамиды (каждое ребро пересекает пирамиду дважды) на П2 совпадают с проекциями самих ребер: п2 = 12 = 2, m2 = 32 = 42., l2 = 52 = 62. Горизонтальные проекции найденных точек находим методом вспомогательных секущих плоскостей:
а) проводим плоскость Г (Г2) через ребро n параллельно основанию пирамиды,
б) строим сечение k пирамиды этой плоскостью: на П2 - k2 =, ана П1 проекция сечения k1 будет представлять собой квадрат, стороны которого параллельны сторонам основания, т.к. боковые грани пирамиды параллельными плоскостями пересекаются по параллельным пря-мым. Для построения этого сечения на находим его вершину - точку 7 сначала на П2 –
72= Г2 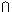 А2 , а затем и на П1 по принадлежности ребру А пирамиды - 71
А2 , а затем и на П1 по принадлежности ребру А пирамиды - 71 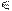 А1.
А1.
в) построив квадрат k1 , по принадлежности ему находим горизонтальные проекции точек 1 и 2.
По аналогичному алгоритму с помощью вспомогательной плоскости Г*(Г*2) находим горизонтальные проекции точек 3, 4, 5, 6.
Профильные проекции найденных вершин находим по двум известным, либо построив для каждой из них прямоугольник ортогонального чертежа (рис.8), либо используя более простой и точный метод, применяемый в инженерной практике. Выбирается базовая плоскость для отсчета нужных размеров вдоль оси y13. Если фигура имеет плоскость симметрии, то базовую плоскость проводят обычно через неё. В нашем варианте за такую плоскость принимаем фронтальную плоскость Ф, проходящую через ось пирамиды, задавая её вырожденными проекциями Ф1 и Ф3. Для построения профильной проекции какой - либо точки (например, 1) замеряется расстояние между Ф1 и 11 (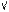 )и откладывается на П3 по соответствующей горизонтальной линии связи от Ф3 вправо (для чего наличие К0 нужно всегда иметь в виду, даже если она не нанесена на чертеже) и получаем проекцию 13 .
)и откладывается на П3 по соответствующей горизонтальной линии связи от Ф3 вправо (для чего наличие К0 нужно всегда иметь в виду, даже если она не нанесена на чертеже) и получаем проекцию 13 .
3. Находим вершины ломаной 9, 10, 11 12, - точки пересечения ребер пирамиды B и D с поверхностью призмы. Находим сначала на П2 как результат пересечения проекций этих ребер пирамиды с вырожденными проекциями граней пm и ml призмы. Проекции этих вершин на П1 и Пз находим по принадлежности ребрам пирамиды сначала на Пз, а затем и на П1 методом, описанным выше..
4. Соединяем найденные вершины отрезками прямых, руководствуясь правилом: соединять отрезками можно только вершины, лежащие в одной грани призмы и одной грани пирамиды. Во избежание ошибок составляем последовательность соединения вершин: 1-5-11-3-9-1 и 2-6-12-4-10-2.
5. Определяем видимость ЛП и ребер поверхностей по представлению. О видимости ЛП на фронтальной проекций уже говорилось выше: видимый и невидимый контуры ЛП совпадают, как и видимые и невидимые ребра пирамиды. При взгляде сверху (на П1) все звенья ЛП видимы, т.к. лежат на видимых боковых гранях пирамиды. Ребра пирамиды являются видимыми, кроме участков 91111 и 101121 , вырезанных отверстием. Ребра призматического отве-рстия проходят внутри пирамиды и невидимы. На П3 видимыми будут звенья ЛП (93 33 113)и (103 43 123), лежащие на видимых слева (см. П2 совместно со стрелкой – направлением взгляда на П3 ) гранях пирамиды AB и AD. Остальные звенья ЛП лежат на невидимых слева гранях пирамиды ВС и СD и являются невидимыми, но т. к. часть пирамиды вырезана, то участки звеньев ЛП 1353 и 2363, которые не закрыты оставшимся материалом пирамиды (ограниченным звеньями 93 33 113 и 103 43 123) будут видны. Видимость ребер поверхностей на П3 такая же, как на П1 .
 8. КРИВЫЕ ЛИНИИ
8. КРИВЫЕ ЛИНИИ
 В начертательной геометрии кривую линию рассматривают как траекторию непрерывно движущейся точки. Кривые могут быть: плоскими и пространственными. Кривые могут быть заданы либо алгебраической или трансцендентной функцией, либо графически. Порядок кривых может быть определен степенью алгебраического уравнения; по числу точек пересечения кривой с прямой линией (для плоских кривых); по числу точек пересечения кривой с плоскостью (для пространственных кривых). В начертательной геометрии кривые линии задаются на чертеже их проекциями.
В начертательной геометрии кривую линию рассматривают как траекторию непрерывно движущейся точки. Кривые могут быть: плоскими и пространственными. Кривые могут быть заданы либо алгебраической или трансцендентной функцией, либо графически. Порядок кривых может быть определен степенью алгебраического уравнения; по числу точек пересечения кривой с прямой линией (для плоских кривых); по числу точек пересечения кривой с плоскостью (для пространственных кривых). В начертательной геометрии кривые линии задаются на чертеже их проекциями.
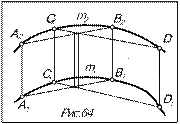
Чтобы определить, какая - плоская или пространственная - кривая задана на чертеже, нужно провести две секущих, одноименные проекции которых бы пересекались, и определить их взаимное положение: если они пересекаются, то кривая плоская, если скрещиваются - пространственная. На рис.64 изображена пространственная кривая, т.к. секущие АВ и CD скрещивающиеся: точки пересечения одноименных проекций не лежат на одной линии связи.
8.11.Плоские кривые. Касательные и нормали
Направление движения точки в каждом ее положении определяется касательной прямой t в данной точке А кривой линии (рис.65).Касательной прямой t в точке A кривой называется предельное положение секущей AA*, когда A* оставаясь на кривой m, стремится к точке A. Кривая называется гладкой, если она во всех своих точках имеет непрерывно изменяющуюся касательную, которая в каждой точке кривой единственная. Нормалью n к кривой в точке A называется прямая, лежащая в плоскости кривой m и перпендикулярная к касательной t этой точке.
На кривых различают особые точки (рис.66):
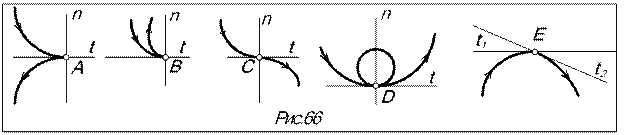 А - точка возврата 1-го рода, В - точка возврата 2-города, С – точка перегиба, D – кратная точка, Е – точка излома.
А - точка возврата 1-го рода, В - точка возврата 2-города, С – точка перегиба, D – кратная точка, Е – точка излома.
8.2.Основные свойства проекций плоских кривых линий
- Порядок плоской алгебраической кривой при параллельном проецировании не изменяется.
- Бесконечно удаленные точки кривой проецируются в бесконечно удаленные точки ее проекции.
- Касательная к кривой проецируется в касательную к ее проекции.
- Точки пересечения плоских кривых проецируются в точки пересечения их проекций.
8.3.Проецирование окружности
Если 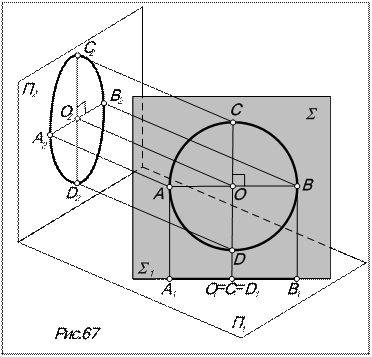 плоскость окружности параллельна какой-либо плоскости проекций, то она проецируется в неё в натуральную ве-личину. В прочих случаях окружность проецируется с искажением.
плоскость окружности параллельна какой-либо плоскости проекций, то она проецируется в неё в натуральную ве-личину. В прочих случаях окружность проецируется с искажением.
Если окружность лежит в про-ецирующей плоскости S (рис.67), то в плоскость проекций, перпен-дикулярную плоскости S, окруж-ность проецируется в виде отрез-ка, равного диаметру окружности (А1В1=АВ) на вырожденной про-екции S1.
В плоскости проекций, к кото-рым плоскость S наклонена, ок-ружность проецируется в виде эл-липса.
При этом:
· центром эллипса О2 является проекция центра О окружности,
· большой осью эллипса будет проекция того диаметра окружности, который параллелен плоскости проекций и проецируется в неё в натуральную величину (С2D2 = CD),
· малой осью эллипса будет проекция того диаметра окружности, который проецируется с наибольшим искажением в рассматриваемую плоскость проекций. На рис.67 это диаметр АВ, который лежит на линии наибольшего наклона плоскости S к П2.
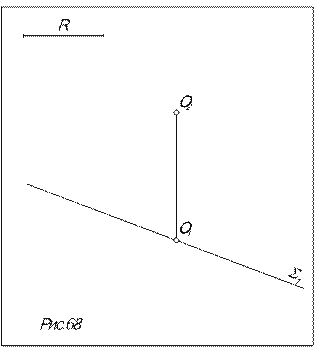 Задача. Построить проекции окружности радиуса R, расположенной в горизонтально проецирующей плоскости S (рис.68).
Задача. Построить проекции окружности радиуса R, расположенной в горизонтально проецирующей плоскости S (рис.68).
Алгоритм решения
1. Так как плоскость S окружности горизонтально проецирующая, то в П1 окружность проецируется в виде отрезка на вырожденной проекции S1 плоскости, длина которого равна 2 R, а на П2 – в эллипс (см. выше рис.67), оси которого– проекции диаметров окружности: большая ось - проекция диаметра CD, который проецируется на П2 в натуральную величину 2 R (лежит на горизонтально проецирующей прямой); малая ось - проекция диаметра АВ, который проецируется с наибольшим искажением (расположен на линии наибольшего наклона к П2, в данном случае это горизонталь, фронтальная проекция которой параллельна оси x12).
2. Для построения случайных точек эллипса П2 заменяем на П4, располагая последнюю параллельно плоскости S окружности (на рис.68 П4 совмещена с плоскостью окружности S):
П2 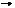 П4
П4  S, П1 / П2 (x12)
S, П1 / П2 (x12) 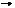 П1 / П4 (s14
П1 / П4 (s14  S1)
S1)
В системе П1 / П4 нам известны обе проекции окружности и можно взять любую точку на окружности, например 14, а затем построить ее проекции в П1 и П2 по алгоритму построения проекции точек при замене плоскостей проекций (см. стр.21, рис.44). Построив 12, можно воспользоваться свойством симметрии эллипса и построить ещё три точки, симметричные 12 относительно осей А2В2 и C2D2. Соединив лекалом построенные на П2 точки, получим эллипс – фронтальную проекцию окружности.
Задача. Построить проекции окружности расположенной в плоскости общего положения (рис.69).
Алгоритм решения
В обе плоскости проекции окружность проецируется в виде эллипсов. Большие оси эллипсов - это проекции диаметров окружности, лежащих на прямых уровня, а малые - проекции диаметров, лежащих на прямых наибольшего наклона плоскости окружности к соответствующей плоскости проекций.
1. Строим горизонтальную проекцию окружности. Большая ось эллипса располагается на горизонтали h*, поэтому на h1* откладываем от проекции центра окружности О1 величины радиуса R (помечено значком 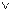 ), и получаем А1В1 – большую ось эллипса. Проводим линию n наибольшего наклона к П1: О1
), и получаем А1В1 – большую ось эллипса. Проводим линию n наибольшего наклона к П1: О1 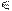 n1 ^ h1*, О2
n1 ^ h1*, О2 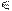 n2
n2 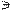 12.
12.
На прямой наибольшего наклона радиус окружности проецируется с искажением и чтобы отложить его, используем способ прямоугольного треугольника (см. стр.10, рис.14):
· определяем НВ отрезка (О1), взяв в качестве первого катета горизонтальную его проекцию (О111), а в качестве второго разность высот D h его концов;
· на гипотенузе О110 (НВ отрезка (О1)) откладываем от точки О1 радиус R (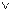 ) и получаем точку С0;
) и получаем точку С0;
· проведя через С0 линию, параллельную h1 , находим на О111 точку С1: отрезок О1С1 – малая полуось эллипса; точку D1, лежащую на другом конце малой оси, находим из условия симметрии - О1С1= О1D1.
Фронтальные проекции точек A, B, C, D находим по принадлежности прямым h2* и n2 соответственно.
2.Строим фронтальную проекцию окружности по аналогичному алгоритму.
 3. Одноименные проекции построенных точек А, В, С, D, E, F, G, H соединяем лекалом дугами эллипса.
3. Одноименные проекции построенных точек А, В, С, D, E, F, G, H соединяем лекалом дугами эллипса.
8.4.Цилиндрическая винтовая линия
Цилиндрическая винтовая линия или гелиса образуется перемещением точки, совершающей равномерное поступательное движение по образующей цилиндра вращения, которая в свою очередь равномерно вращается вокруг оси цилиндра. Винтовая линия задается радиусом основания R цилиндра и шагом h – величиной перемещения точки по образующей при повороте её вокруг оси на 3600 (рис.70).
Чтобы построить проекции винтовой линии, окружность и шаг разбиваются на n равных частей  (например, на 8, как на рис.70). Поворот точки на 1/n части окружности соответствует ее перемещению вдоль оси цилиндра на 1/n части шага: если формирующая кривую точка А из исходного положения (0) переместится в положение 1, то проекция А1 окажется в точке 1 окружности, а её фронтальная проекция А2 – на горизонтали под тем же номером. Последовательно перемещая горизонтальную проекцию точки А1 в следующие положения, строим соответствующие фронтальные её проекции, соединив которые плавной кривой получаем фронтальную проекцию винтовой линии – синусоиду.
(например, на 8, как на рис.70). Поворот точки на 1/n части окружности соответствует ее перемещению вдоль оси цилиндра на 1/n части шага: если формирующая кривую точка А из исходного положения (0) переместится в положение 1, то проекция А1 окажется в точке 1 окружности, а её фронтальная проекция А2 – на горизонтали под тем же номером. Последовательно перемещая горизонтальную проекцию точки А1 в следующие положения, строим соответствующие фронтальные её проекции, соединив которые плавной кривой получаем фронтальную проекцию винтовой линии – синусоиду.
|
|