Функции. Каждому элементу множества ставится в соответствие по некоторому закону единственный элемент множества

Каждому элементу множества 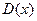ставится в соответствие по некоторому закону 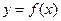единственный элемент множества 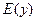. Функция задается аналитически или графически. Монотонная функция имеет обратную функцию. Различают четные, нечетные и функции общего вида.

Определение. (По Коши) 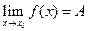, если определена в некоторой окрестности точки 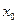, быть может кроме самой этой точки, и если .

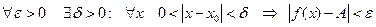В определении предела удобно использовать вместо неравенств понятия окрестностей .

Введем обозначения:

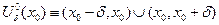- выколотая окрестность числа 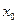размера .

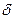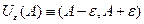- окрестность числа 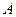размера .

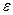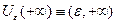- окрестность 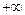размера .

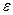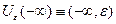- окрестность 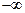размера .

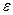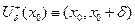- правая половины окрестности числа 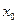размера .

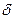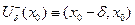- левая половины окрестности числа 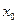размера .

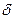Определение. 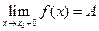, если определена на правой половине окрестности точки 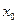, быть может кроме самой этой точки, и если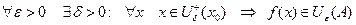

Определение*. (По Гейне) 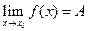, если .

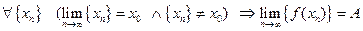Теорема. Определения по Коши и по Гейне эквивалентны.

Пример. Доказать по определению .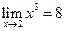

Запишем определение: 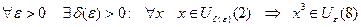. Когда значения нашей функции принадлежат 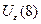, аргумент 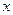принадлежит интервалу 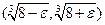. Нам необходимо найти максимальный размер окрестности принадлежащий указанному интервалу. Окрестность - интервал симметричный относительно числа 2. Используя график функции и изображения окрестностей, находим, что .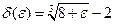

Пример. Доказать, что .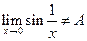

Сформулируем отрицание к определению предела по Гейне: 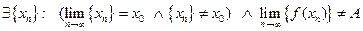. Оно выполняется для последовательности 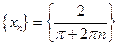, которая сходится к нулю, а последовательность не имеет конечного предела (можно показать при помощи Критерия Коши).

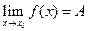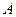Теорема. Если , где - конечное число, то на некоторой окрестности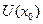 -ограничена, то есть .

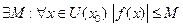Доказательство. Пусть 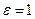, тогда 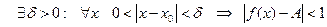. Преобразуем последнее неравенство: 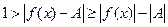. Отсюда имеем, что для любого 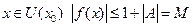, т.е. функция ограничена числом 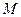. Теорема доказана.

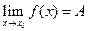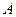Теорема. (О сохранении знака). Если , где - конечное число, то на некоторой окрестности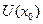 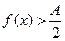, есл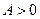и , и 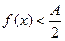, если .

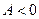Доказательство. Пусть 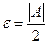, тогда 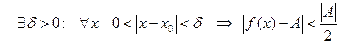. Последнее неравенство запишем в виде: 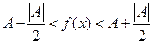. Если 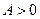, то из левого неравенства имеем 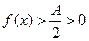. Если 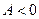, то из правого неравенства имеем 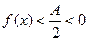. Теорема доказана.

Теорема. (О зажатой функции). Если 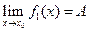, и на некоторой окрестности 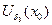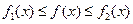, тогда .

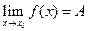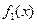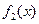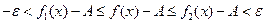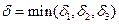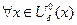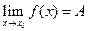Доказательство. Используя последнее неравенство и определения пределов функций и , запишем: . Из этого выражения следует, что для и выполняется неравенство . Таким образом, . Теорема доказана.

Теорема. Пусть 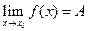и 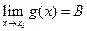, тогда:

1) ;

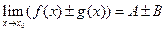2) ;

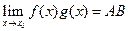3) .

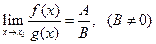Теорема легко доказывается с использованием определения предела по Гейне и аналогичной теоремы для последовательностей.

Теорема. (Критерий Коши). Для того, чтобы существовал конечный предел 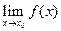, необходимо и достаточно, чтобы была определена в некоторой окрестности точки 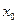, быть может кроме самой этой точки, и .

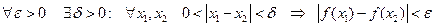(Без доказательства).