Множество действительных чисел.

Понятия действительных чисел, их свойства формулировались в течение длительного времени. Аксиоматический подход к понятию действительных чисел заключается в том, что действительными числами называют множество, элементы которого обладают следующими свойствами (удовлетворяют следующим аксиомам).

I. Аксиомы сложения.

1. 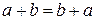- переместительный.

2. 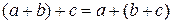- сочетательный.

3. 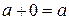- существует «0».

4. 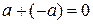- существует противоположное число.

II. Аксиомы умножения.

1. 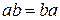- - переместительный.

2. 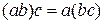- сочетательный.

3. 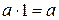- существует «1».

4. 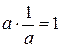- существует обратное число.

5. 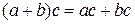- распределительный.

III. Аксиомы порядка.

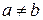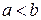1. Если , то или .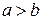

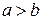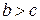2. Если и , то .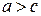

3. Если 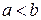, то .

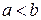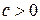4. Если и , то .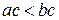

IV. Аксиома Архимеда.

1. Для любого 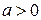существует 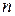, удовлетворяющее неравенству .

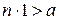V. Аксиома непрерывности.

1. Для всякой системы вложенных числовых отрезков, стремящихся к нулю, существует единственное число, принадлежащее всем отрезкам данной системы. (Непрерывность в смысле Кантора).

Определение. Система числовых отрезков 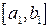, , 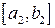…, 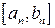называется системой вложенных отрезков, если .

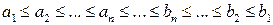Определение. Длина вложенных отрезков 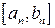стремится к нулю, если .

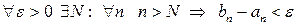Теперь будем рассматривать только множества, состоящие из действительных чисел.

Определение. 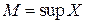( 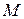- точная верхняя грань множества ).

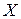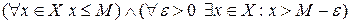
Определение. 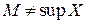(отрицание к предыдущему определению).

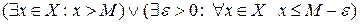
Определение. Множество 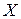ограничено сверху, если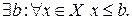

Определение. Множество 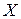ограничено, если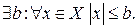

Теорема. Всякое ограниченное сверху не пустое множество имеет точную верхнюю грань.

Доказательство. Внутри множества возьмем произвольную точку 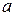. Это можно сделать, т. к. наше множество не пустое. Возьмем произвольную точку 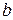правее нашего множества. Это можно сделать, т. к. наше множество ограничено сверху. Отрезок 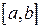делим пополам и выбираем правый из половинок, содержащих точки множества 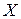, или левый, если правый не содержит точек из 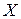. Выбранный отрезок обозначаем 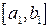. Разбиваем отрезок 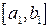пополам и указанным способом выбираем отрезок 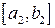. Продолжая разбиения получим систему вложенных отрезков, длина которых стремится к нулю. Действительно,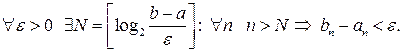

Полученная система вложенных отрезков, стремящихся к нулю, в соответствие с аксиомой V, имеет общую точку 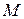. Покажем, что 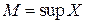. Для этого надо показать, что выполняются два высказывания из определения супремума.

1). 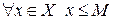. Предположим обратное. Пусть 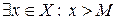. Тогда . Но при 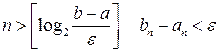, т. е. 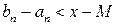. Учитывая, что 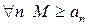, последнее неравенство можно представить в виде: 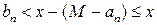. Мы пришли к противоречию т. к. 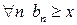. Значит наше предположение не верно, т.е. первое высказывание выполняется.

2). 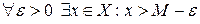. Действительно, т.к. длина отрезков стремится к нулю, то 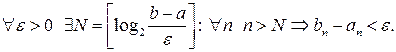Учитывая, что 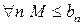и , усилим последнее неравенство: 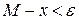. Мы получили: .

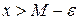Таким образом 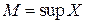. Теорема доказана.

Доказательство*. Заметим, что все отрезки содержат элементы множества, и правая точка отрезка лежит правее элементов множества или, по крайней мере, совпадает с правой точкой множества. Надо показать, что 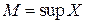, т.е. все элементы множества лежат левее 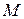или 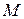является правой точкой множества, а также между точками множества и точкой 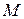отсутствует зазор.

Пусть какая-то точка 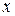множества лежит правее точки 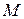, тогда длина отрезка системы с номером 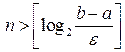меньше расстояния между точкой 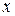и точкой 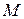, т. е. точка 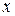лежит правее точки 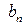. Противоречие.

Предположим теперь наличие зазора между элементами множества и точкой 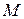, тогда все отрезки системы не могут по длине быть меньше этого зазора, т.к. они содержат и точку 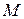и хотя бы одну точку множества, что противоречит сходимости системы отрезков. Теорема доказана.