
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Условия наблюдения интерференции
|
|
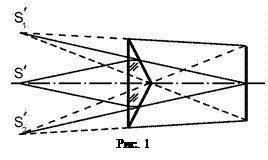 Как известно, обычно интерференция света наблюдается редко, так как выполнить условия когерентности достаточно сложно. Для этих целей используются специальные устройства – интерферометры, в которых приняты специальные меры, чтобы обеспечить эти условия. Для получения интерференции существуют два основных метода – делением амплитуды и делением волнового фронта. Примером первого случая является рассмотренный ранее интерферометр Майкельсона, в котором волна на полупрозрачном зеркале делится по амплитуде на две ветви, которые направляются в разные каналы. Затем они объединяются вновь и дают интерференционную картину. Деление волнового фронта можно осуществить с помощью бипризмы Френеля (рис. 1). Здесь формируются два когерентных пучка, идущих в различных направлениях, которые интерферируют в зоне их перекрытия.
Как известно, обычно интерференция света наблюдается редко, так как выполнить условия когерентности достаточно сложно. Для этих целей используются специальные устройства – интерферометры, в которых приняты специальные меры, чтобы обеспечить эти условия. Для получения интерференции существуют два основных метода – делением амплитуды и делением волнового фронта. Примером первого случая является рассмотренный ранее интерферометр Майкельсона, в котором волна на полупрозрачном зеркале делится по амплитуде на две ветви, которые направляются в разные каналы. Затем они объединяются вновь и дают интерференционную картину. Деление волнового фронта можно осуществить с помощью бипризмы Френеля (рис. 1). Здесь формируются два когерентных пучка, идущих в различных направлениях, которые интерферируют в зоне их перекрытия.
Цвета тонких пленок. Так как подавляющее большинство источников не когерентно и условия когерентности в природе осуществляются крайне редко, но, тем не менее, интерференционные эффекты, наблюдаемые без специальных приспособлений, существуют - к ним относятся, например, цвета тонких пленок. Под тонкой пленкой подразумевается слой прозрачного вещества толщиной в несколько микрон, при этом интерферируют световые потоки, отраженные от его нижней и верхней поверхности. Примерами таких эффектов могут служить пятна бензина на лужах, переливающаяся окраска поверхности мыльных пузырей, цвета побежалостей на металлах и т.п. При такой интерференции различают два случая - полосы равной толщины и полосы равного наклона.
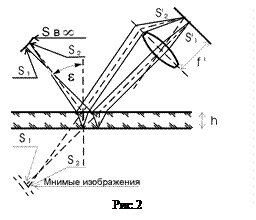 1. Полосы равного наклона. Возникают в фокальной плоскости линзы (или, что эквивалентно, в бесконечности) при освещении плоскопараллельной пластинки (пленки с параллельными гранями) световым пучком от удаленного, но имеющего конечный угловой размер, источника
1. Полосы равного наклона. Возникают в фокальной плоскости линзы (или, что эквивалентно, в бесконечности) при освещении плоскопараллельной пластинки (пленки с параллельными гранями) световым пучком от удаленного, но имеющего конечный угловой размер, источника 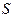 (рис 2). При этом, в каждую точку задней фокальной плоскости линзы попадают группы лучей, вышедшие лишь из одной точки источника (в
(рис 2). При этом, в каждую точку задней фокальной плоскости линзы попадают группы лучей, вышедшие лишь из одной точки источника (в 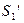 из
из 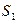 , а в
, а в 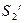 из
из 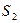 ), поэтому они когерентны и интерферируют. Если в качестве линзы представить себе глаз наблюдателя, аккомодированного на бесконечность, то ему будет казаться, что он видит два мнимых изображения источника света, наложенных друг на друга и слегка сдвинутых на величину смещения лучей, отраженных от разных граней. Разность хода между каждой парой лучей возникает из-за того, что один из лучей проходит пластинку с показателем преломления
), поэтому они когерентны и интерферируют. Если в качестве линзы представить себе глаз наблюдателя, аккомодированного на бесконечность, то ему будет казаться, что он видит два мнимых изображения источника света, наложенных друг на друга и слегка сдвинутых на величину смещения лучей, отраженных от разных граней. Разность хода между каждой парой лучей возникает из-за того, что один из лучей проходит пластинку с показателем преломления 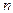 , отличным от показателя окружающей ее среды (для простоты воздуха). Выражение для этой разности хода
, отличным от показателя окружающей ее среды (для простоты воздуха). Выражение для этой разности хода 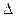 хорошо известно и описывается выражением
хорошо известно и описывается выражением
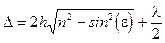 , ,
| (1) |
где 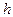 - толщина пластинки,
- толщина пластинки, 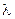 - длина волны излучения,
- длина волны излучения, 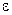 - угол падения; слагаемое
- угол падения; слагаемое 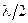 появляется из-за потери половины длины волны при отражении.
появляется из-за потери половины длины волны при отражении.
В рассматриваемом случае при освещении монохроматическим источником единственным переменным параметром, определяющим разность хода, является угол падения 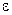 , откуда и произошло название такого типа интерференции - полосы равного наклона. Максимумы интерференционной картины возникнут в тех точках фокальной плоскости, в которых соберутся группы лучей с разностью хода равной целому числу длин волн. Это произойдет при таких углах падения
, откуда и произошло название такого типа интерференции - полосы равного наклона. Максимумы интерференционной картины возникнут в тех точках фокальной плоскости, в которых соберутся группы лучей с разностью хода равной целому числу длин волн. Это произойдет при таких углах падения 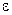 , которые удовлетворяют условию (2) при
, которые удовлетворяют условию (2) при 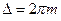 , где
, где 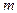 - целое число. Таким образом, форма интерференционных полос будет определяться геометрическим местом точек, в которых выполняется это условие. Так как в данной ситуации имеется ось симметрии - оптическая ось линзы, то интерференционная картина имеет вид концентрических окружностей с центром в фокусе линзы F’. При освещении немонохроматическим источником для каждой длины волны
- целое число. Таким образом, форма интерференционных полос будет определяться геометрическим местом точек, в которых выполняется это условие. Так как в данной ситуации имеется ось симметрии - оптическая ось линзы, то интерференционная картина имеет вид концентрических окружностей с центром в фокусе линзы F’. При освещении немонохроматическим источником для каждой длины волны 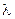 возникнет своя система колец, и результирующая картина интерференции будет иметь радужную окраску.
возникнет своя система колец, и результирующая картина интерференции будет иметь радужную окраску.
Полосы равной толщины. Иная ситуация возникает, если линза установлена таким образом, что в плоскость изображения проецируется поверхность пленки, т.е. отрезки, определяющие положение линзы удовлетворяют формуле Гаусса
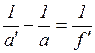 , ,
| (2) |
 где
где 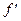 - фокусное расстояние линзы. Пленка при этом может иметь неодинаковую толщину. В этом случае в каждой точке изображения собираются множество пар пучков лучей, вышедших из разных точек источника
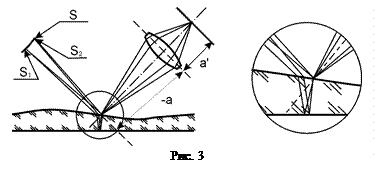
- фокусное расстояние линзы. Пленка при этом может иметь неодинаковую толщину. В этом случае в каждой точке изображения собираются множество пар пучков лучей, вышедших из разных точек источника 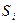 , но лучи в этих парах когерентны между собой и все они имеют почти одинаковую разность хода, обусловленную толщиной пленки в том месте, которое сопряжено с данной точкой изображения. Положения интерференционных картин от каждой пары лучей будут совпадать, и суммарная картина будет идентична каждой отдельной, только намного ярче. Вообще говоря, разность хода пар от различных точек источника будет немного отличаться, так как разные лучи, прошедшие сквозь пленку для того, чтобы попасть в точку на верхней грани, сопряженную с точкой на экране, должны пройти разным путем (рис. 3 справа). Однако если источник света удален, а рельеф поверхности пленки достаточно гладкий, то различия в разностях хода будут пренебрежимо малы. Как правило, на практике такие условия выполняются.
, но лучи в этих парах когерентны между собой и все они имеют почти одинаковую разность хода, обусловленную толщиной пленки в том месте, которое сопряжено с данной точкой изображения. Положения интерференционных картин от каждой пары лучей будут совпадать, и суммарная картина будет идентична каждой отдельной, только намного ярче. Вообще говоря, разность хода пар от различных точек источника будет немного отличаться, так как разные лучи, прошедшие сквозь пленку для того, чтобы попасть в точку на верхней грани, сопряженную с точкой на экране, должны пройти разным путем (рис. 3 справа). Однако если источник света удален, а рельеф поверхности пленки достаточно гладкий, то различия в разностях хода будут пренебрежимо малы. Как правило, на практике такие условия выполняются.
В рассматриваемом случае при монохроматическом источнике переменным параметром будет толщина пленки 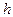 , т.е. по аналогии предыдущему случаю, максимумы интерференционной картины будут в тех местах пленки (а, следовательно, и в плоскости изображения) где разность хода
, т.е. по аналогии предыдущему случаю, максимумы интерференционной картины будут в тех местах пленки (а, следовательно, и в плоскости изображения) где разность хода 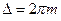 , где
, где 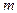 - целое число. Совокупность этих максимумов определяет форму интерференционных полос, которая представляет собой геометрическое место точек на поверхности пленки, в которых ее толщина одинакова и такова, что выполняется условие
- целое число. Совокупность этих максимумов определяет форму интерференционных полос, которая представляет собой геометрическое место точек на поверхности пленки, в которых ее толщина одинакова и такова, что выполняется условие 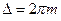 . Это обстоятельство дало название такому типу интерференционных полос - полосы равной толщины.
. Это обстоятельство дало название такому типу интерференционных полос - полосы равной толщины.
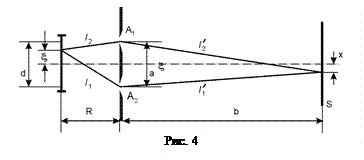 Условия когерентности протяженного некогерентного источника света. Выясним условия, при которых протяженный источник некогерентного света становится когерентным. Для этого рассмотрим опыт Юнга (рис. 4). Источник света длиной
Условия когерентности протяженного некогерентного источника света. Выясним условия, при которых протяженный источник некогерентного света становится когерентным. Для этого рассмотрим опыт Юнга (рис. 4). Источник света длиной 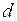 освещает два узких одинаковых отверстия, причем они малы настолько, что разность хода между
освещает два узких одинаковых отверстия, причем они малы настолько, что разность хода между
крайними лучами в них много меньше половины длины волны. Расстояние от щелей до экрана 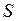 и источника велико по сравнению с размером источника, расстоянием между щелями и предполагаемой областью интерференции, т.е.
и источника велико по сравнению с размером источника, расстоянием между щелями и предполагаемой областью интерференции, т.е.
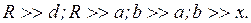
| (3) |
Определим разность хода между лучами, идущими через щели  и
и 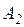 , исходящих от бесконечно малого участка источника света, находящегося на расстоянии
, исходящих от бесконечно малого участка источника света, находящегося на расстоянии 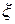 от оси
от оси
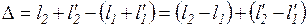 ; ;
| (4) |
Из треугольников
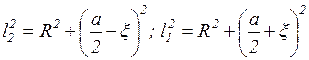 , ,
| (5) |
откуда 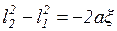 , но
, но 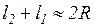 . Следовательно
. Следовательно
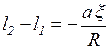 . .
| (6) |
По аналогии
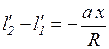 . .
| (7) |
Таким образом, разность фаз между лучами
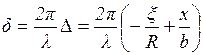 . .
| (8) |
Обе волны когерентны, т.к. исходят из одного источника и их интенсивности равны, поскольку они проходят одинаковые щели. Источником является его бесконечно малый участок, поэтому интенсивность этих волн 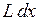 , где
, где 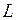 линейная яркость источника (
линейная яркость источника (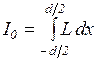 интенсивность, создаваемая всем источником). Таким образом, освещенность
интенсивность, создаваемая всем источником). Таким образом, освещенность 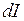 , создаваемая на экране участком источника будет
, создаваемая на экране участком источника будет
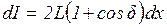 . .
| (9) |
Распределение освещенности на экране  , создаваемое всем источником, получится в результате вычисления интеграла
, создаваемое всем источником, получится в результате вычисления интеграла
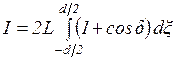 . .
| (10) |
Подставляя в (10) значение фазы 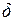 из (8) и выполняя интегрирование, получим
из (8) и выполняя интегрирование, получим
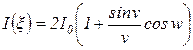 , (11)
, (11)
где 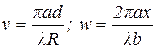 .
.
Определим контраст этого распределения. Обозначив 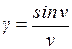 , найдем, что
, найдем, что
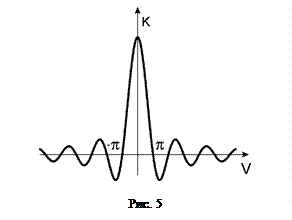
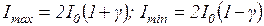 .
.
Подставляя эти значения в формулу для контраста 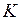 найдем, что
найдем, что 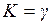 . Зависимость контраста от
. Зависимость контраста от 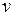 приведена на рис. 5. При увеличении
приведена на рис. 5. При увеличении 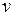 контраст уменьшается, поскольку складываются когерентные и некогерентные волны. Интересный эффект возникает при
контраст уменьшается, поскольку складываются когерентные и некогерентные волны. Интересный эффект возникает при  , т.н. «реверс контраста» - получается негативное изображение интерференционной картины. Величину
, т.н. «реверс контраста» - получается негативное изображение интерференционной картины. Величину 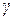 называют также степенью когерентности или видностью интерференционной картины.
называют также степенью когерентности или видностью интерференционной картины.
Из рис. 5 видно, что высокий контраст получается при 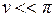 или
или
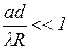 . .
| (12) |
 Эта оценка является условием, когда некогерентный источник можно считать когерентным. Рассмотрим его подробнее. На рис. 6 обозначены:
Эта оценка является условием, когда некогерентный источник можно считать когерентным. Рассмотрим его подробнее. На рис. 6 обозначены: 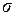 - апертурный угол,
- апертурный угол, 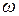 - угловой размер предмета. Условие (12) можно записать двумя способами.
- угловой размер предмета. Условие (12) можно записать двумя способами.
1. 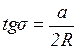 , тогда условие когерентности будет
, тогда условие когерентности будет 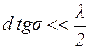 , но так как угол
, но так как угол 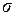 мал, то
мал, то 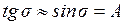 , где
, где 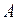 -апертура, и окончательно это условие будет выглядеть как
-апертура, и окончательно это условие будет выглядеть как
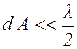 . .
| (13) |
2. В случае удаленного источника 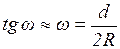 и условие когерентности будет
и условие когерентности будет
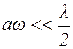 . .
| (14) |
К примеру, полагая 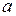 неким характерным размером входного зрачка прибора, можно определить при каких условиях Солнце можно считать когерентным источником для этого прибора. Известно, что угловой размер Солнца
неким характерным размером входного зрачка прибора, можно определить при каких условиях Солнце можно считать когерентным источником для этого прибора. Известно, что угловой размер Солнца 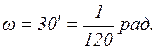 , а средняя длина волны излучения
, а средняя длина волны излучения 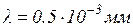 , то из (14) получится, что
, то из (14) получится, что 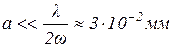 .
.
|
|