Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Евклидово пространство
|
|
Линейное пространство Rn векторов над полем Р вещественных чисел называется евклидовым, если в нем определена операция скалярного произведения, где каждой паре векторов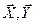 
Î Rn поставлено в соответствие число, обозначаемое через 
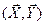и обладающее следующими свойствами:
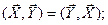
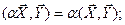
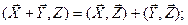
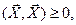и 
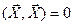только если 
.
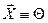Ортонормированный базис это базис {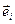 
, i =1, …, n }, где (, 
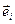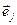)=0; (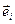, 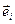)=1
В ортонормированном базисе координаты вектора могут быть выражены через скалярное произведение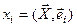 
, т.е. xi является проекцией вектора 
на вектор 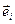. Действительно, 
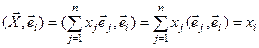, поскольку в силу ортонормированности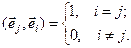 
В ортонормированном и только в ортонормированном базисе евклидового пространства для векторов – столбцов чисел – скалярное произведение может быть определено как 
, где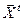 
-вектор строка.
По аналогии с трехмерным пространством можно определить понятие длины или модуля вектора:
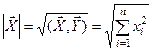, и угла между векторами: 
.
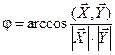Скалярное произведение в произвольном базисе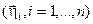 
представляется более сложной функциональной зависимостью
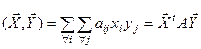, где 
Пример. Пусть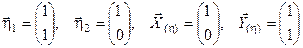 
, (рис. 7.2).
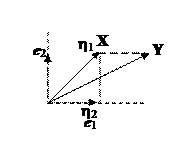Матрица коэффициентов
В результате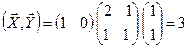 
.
| Рис. 7.2. Произвольный базис |
В пространстве С [ a, b ] функций, определенных на отрезке [ a, b ] скалярное произведение
.
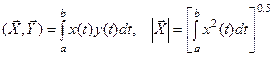Из соотношений, характеризующих скалярное произведение векторов в пространстве непрерывных функций, следуют очень полезные в практических приложениях для предельных оценок
|
|