
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задание 3. Приближенное интегрирование с заданным шагом
|
|
Приближенное интегрирование с заданным шагом
1. Цель работы
Изучение способов приближенного интегрирования
2. Основные теоретические положения
2.1. Постановка задачи
Пусть необходимо вычислить определенный интеграл
I =  . (13)
. (13)
Методы приближенного интегрирования основаны на использовании геометрической интерпретации значения определенного интеграла, как площади криволинейной трапеции, ограниченной осью абсцисс, прямыми x = a, x = b и кривой f (x) (рис.2).
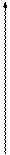 f (x) f (x)
f (x) f (x)







 x 0 a b
x 0 a b
Рис.2
Для вычисления интересующей нас площади (см. рис.3) разобьем область интегрирования на n равных частей точками:
x = a, x 1, x 2,..., x i, xi +1,..., x n = b. (14)
 f (x) f (x) Рис.3
f (x) f (x) Рис.3
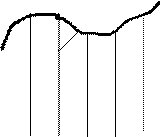


I i



 x
x
0 х = a х i x i+1 х = b
Тогда I = 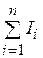 ,
,
где Ii = 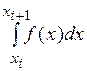 . (15)
. (15)
Значит, для вычисления интеграла (13) необходимо вычислить n площадей фигур криволинейных трапеций (рис.3).
2.2. Интегрирование функций, полученных из экспериментальных данных
Как правило, в результате эксперимента получают дискретные данные, т.е. в узлах хi производят измерение значений некоторой функции yi, (см.работу 1).
Интегрирование дискретных данных включает в себя предварительную аппроксимацию или интерполяцию этих данных известной функцией с последующим ее интегрированием. В большинстве случаев не удается подобрать одну функцию для аппроксимации на всем интервале, поэтому область интегрирования разделяется на большое количество подинтервалов, на каждом из которых используется простая функция типа линейной, квадратической или кубической. После чего результаты аппроксимации для отдельных подинтервалов складываются вместе для получения полного интеграла.
Рассмотрим три простейших метода приближенного интегрирования.
2.3. Типы формул интегрирования
Наиболее часто при численном интегрировании используются метод прямоугольников, метод трапеций, интегрирование по Ромбергу, метод Симпсона и квадратура Гаусса. Каждый из этих методов является более точным, чем предыдущий, поскольку производит аппроксимацию данных более сложной кривой.
2.4. Метод прямоугольников
Согласно методу прямоугольников, область между точками разбиения интервала интегрирования [ a, b ] заменяется прямоугольником, высота которого соответствует координате Y одной из точек, а ширина равна расстоянию между точками. Значение интеграла определяется по следующей формуле:
I =  . (16)
. (16)
Такое приближение может показаться грубым, однако при малой ширине интервала и гладкой функции результаты получаются достаточно точными. Кроме того, такой метод очень просто реализовать, поскольку достаточно просто вычисляется площадь прямоугольника – перемножается значение Y в каждой точке на ширину интервала и результаты складываются.
2.5. Метод трапеций
Согласно этому методу, каждая пара соседних точек соединяется прямой линией, образуя последовательность трапеций.
Площадь трапеции равняется полусумме оснований, умноженной на высоту, которая в данном случае равна расстоянию между точками по оси Х. Интеграл равен сумме площадей всех трапеций.
I =  . (17)
. (17)
2.6. Метод Симпсона
Согласно правилу Симпсона, для аппроксимации данных используется уравнение параболы, построенной по трем точкам (правило 1/3) или по четырем точкам (правило 3/8).

 (18)
(18)
I =  . (19)
. (19)
Пример 1.
Вычислить определенный интеграл

с помощью методов прямоугольников и трапеций с числом шагов, равным 5. Сравнить результаты вычислений двумя методами. (Истинное значение интеграла равно 3.208).
○ Метод прямоугольников

Для удобства запишем значения функции в узлах в таблицу.
| xi | f (xi) слева | f (xi) справа |
| 0.5 0.667 0.75 0.8 | 0.5 0.667 0.75 0.8 0.833 | |
| Σ | 2.717 | 3.55 |
График подинтегральной функции выглядит следующим образом:
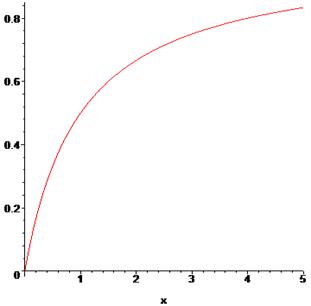
Значение интеграла (слева) просто равно сумме значений 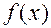 в узлах, т.к. шаг
в узлах, т.к. шаг 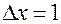 и равно 2.717, значение интеграла (справа) = 3.55.
и равно 2.717, значение интеграла (справа) = 3.55.
Среднее значение интеграла равно (2.717+3.55)/2 = 3.1335.
Метод трапеций

Таблица значений получается, по сути дела, той же самой
| xi | f (xi) |
| 0.5 0.667 0.75 0.8 0.833 |
И значение интеграла
 ●
●
|
|