
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Модуль 1 Случайные события.
|
|
ТГР ПГ 4 семестр
Математика.
Модуль 1 Случайные события.
11.1. Номер автомобиля состоит из трех букв и трех цифр. Сколько различных номеров можно составить, используя 10 цифр и алфавит в 30 букв.
Решение. Очевидно, что количество всех возможных комбинаций из 10 цифр по 4 равно 10.000.
Число всех возможных комбинаций из 30 букв по две равно числу размещений из m по n
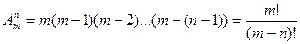
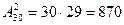 .
.
Если учесть возможность того, что буквы могут повторяться, то число повторяющихся комбинаций равно 30 (одна возможность повтора для каждой буквы). Итого, полное количество комбинаций по две буквы равно 900.
Если к номеру добавляется еще одна буква из алфавита в 30 букв, то количество комбинаций увеличивается в 30 раз, т.е. достигает 27.000 комбинаций.
Окончательно, т.к. каждой буквенной комбинации можно поставить в соответствие числовую комбинацию, то полное количество автомобильных номеров равно 270.000.000.
11.2. При перевозке ящика, в котором содержались 21 стандартная я 10 нестандартных деталей, утеряна одна деталь, причем неизвестно какая. Наудачу извлеченная (после перевозки) из ящика деталь оказалась стандартной. Найти вероятность того, что была утеряна:
а) стандартная деталь; б) нестандартная деталь.
Решение а) Извлеченная стандартная деталь, очевидно, не могла быть утеряна; могла быть потеряна любая из остальных 30 деталей (21+10-1=30), причем среди них было 20 стандартных (21—1=20). Вероятность того, что была потеряна стандартная деталь, Р = 20/30 =.2/3.
б) Среди 30 деталей, каждая из которых могла быть утеряна, было 10 нестандартных. Вероятность того, что потеряна нестандартная деталь Р == 10/30= 1/3.
11.3. Найти вероятность того, что при бросании трех игральных костей шестерка выпадет на одной (безразлично какой) кости, если на гранях двух других костей выпадут числа очков, не совпадающие между собой (и не равные шести).
Решение. Общее число элементарных исходов испытания равно числу сочетаний из шести элементов по три, т. е. 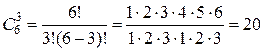 .
.
Число исходов, благоприятствующих появлению шестерки на одной грани и различного числа очков (не равного шести) на гранях двух других костей, равно числу сочетаний из пяти элементов по два, т. е. 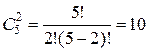 .
.
Искомая вероятность равна отношению числа исходов, благоприятствующих интересующему нас событию, к общему числу возможных элементарных исходов: 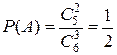 .
.
11.4 Два лица 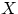 и
и 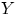 условились встретиться в определённом месте между двумя и тремя часами дня. Пришедший первым ждет другого в течение 10 минут, после чего уходит. Чему равна вероятность встречи этих лиц, если каждый из них может прийти в любое время в течение указанного часа независимо от другого?
условились встретиться в определённом месте между двумя и тремя часами дня. Пришедший первым ждет другого в течение 10 минут, после чего уходит. Чему равна вероятность встречи этих лиц, если каждый из них может прийти в любое время в течение указанного часа независимо от другого?
Решение. Будем считать интервал с 14 до 15 часов отрезком [0, 1] длиной в 1 час. Пусть 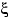 («кси») и
(«кси») и 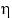 («эта») — моменты прихода
(«эта») — моменты прихода 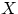 и
и 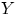 — точки отрезка [0, 1]. Все возможные результаты эксперимента — точки квадрата со стороной 1:
— точки отрезка [0, 1]. Все возможные результаты эксперимента — точки квадрата со стороной 1: 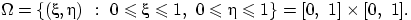

Можно считать, что эксперимент сводится к бросанию точки наудачу в квадрат. При этом благоприятными исходами являются точки множества 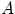 :
:
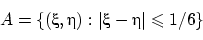
(10 минут = 1/6 часа). Попадание в множество  наудачу брошенной в квадрат точки означает, что
наудачу брошенной в квадрат точки означает, что  и
и 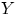 встретятся. Тогда вероятность встречи равна
встретятся. Тогда вероятность встречи равна
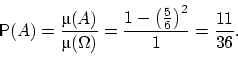
11.5. На стеллаже библиотеки в случайном порядке расставлено 15 учебников, причем пять из них в переплете. Библиотекарь берет наудачу три учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете (событие А).
Решение.
Первый способ. Требование—хотя бы один из трех взятых учебников в переплете будет осуществлено, если произойдет любое из следующих трех несовместных событий:
В —один учебник в переплете, С—Два учебника в переплете, D —три учебвика в переплете.
Интересующее нас событие А можно представить в виде суммы событий: А = B + C + D. По теореме сложения,
Р (А)=Р (В)+Р (С)+P(D).
Найдем вероятности событий В, С и D:
Р (В) = 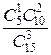 = 45/91, Р (С)=
= 45/91, Р (С)= 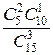 = 20/91, P (0) =
= 20/91, P (0) = 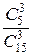 = 2/91
= 2/91
Подставив эти вероятности, окончательно получаем
Р(А) = 45/91 +20/91 +2/91 ==67/91.
Второй способ. События А (хотя бы один из взятых трех учебников имеет переплет) и А (ни один из взятых учебников не имеет переплета) — противоположные, поэтому
Р (А) = 1 —Р (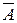 ).
).
Вероятность появления события А (ни один из взятых учебников не имеет переплета)
Р(А)= 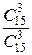 =24/91.
=24/91.
Искомая вероятность
Р (А ) = 1—24/91 =67/91.
11.6. В читальном зале имеется шесть учебников по теории вероятностей, из которых три в переплете. Библиотекарь наудачу взял два учебника. Найти вероятность
того, что оба учебника окажутся в переплете.
Решение. Введем обозначения событий: А—первый. Взятый учебник имеет переплет, В—второй учебник имеет переплет. Вероятность того, что первый учебник имеет переплет, Р(А) = 3/6 = 1/2.
Вероятность того, что второй учебник имеет переплет, при условии, что первый взятый учебник был в переплете, т. е. условная вероятность события В, такова: Р(B/A) = 2/5.
Искомая вероятность того, что оба учебника имеют переплет, по
теореме умножения вероятностей событий равна
Р (АВ): =Р (А) Р(B/A) = 1/2.2/5 = 0, 2.
11.7 В электрическую цепь последовательно включены три элемента, работающие независимо один от другого. Вероятности отказов первого, второго и третьего элементов соответственно равны: р1 = 0, 1; р2 = 0, 15; р3 = 0, 2.
Найти вероятность того, что тока в цепи не будет.
Решение. Элементы включены последовательно, поэтому тока в цепи не будет (событие А), если откажет хотя бы один из элементов.
Искомая вероятность Р (А) = 1-q1 q2 q3=1- (1-0, 1) (1 -0, 15) (1-0, 2) = 0, 388.
11.8. Есть три завода, производящих одну и ту же продукцию. При этом первый завод производит 25%, второй завод — 35% и третий — 40% всей производимой продукции. Брак составляет 5% от продукции первого завода, 3% от продукции второго и 4% от продукции третьего завода. Вся продукция смешивается и поступает в продажу. Найти вероятность купить бракованное изделие.
Решение Изделие выбирается наудачу из всей произведённой продукции. Воспользуемся формулой полной вероятности. Рассмотрим три гипотезы:  ,
, 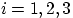 . Вероятности этих событий даны:
. Вероятности этих событий даны: 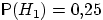 ,
, 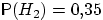 ,
, 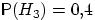 .
.
Пусть 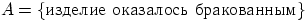 . Даны также условные вероятности
. Даны также условные вероятности 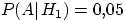 ,
, 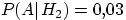 ,
, 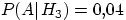 .
.
Вероятность равна доле бракованных изделий в объеме всей продукции, т.е.

= 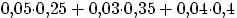 .
.
11.9 Два стрелка подбрасывают монетку и выбирают, кто из них стреляет по мишени (одной пулей). Первый стрелок попадает по мишени с вероятностью 1, второй стрелок — с вероятностью 0, 00001. Предположим, что мишень поражена. Какова вероятность того, что это попал первый стрелок?
Решение. Можно сделать два предположения об эксперименте: 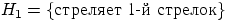 и
и 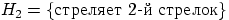 . Априорные (до опыта) вероятности этих гипотез одинаковы:
. Априорные (до опыта) вероятности этих гипотез одинаковы: 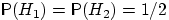 .
.
Рассмотрим событие 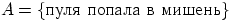 . Известно, что
. Известно, что
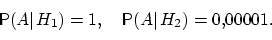
Вероятность пуле попасть в мишень
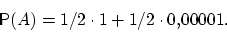
Предположим, что событие  произошло. Очевидно, что вероятность того, что при этом попал первый стрелок, вычисляется по формуле Байеса
произошло. Очевидно, что вероятность того, что при этом попал первый стрелок, вычисляется по формуле Байеса
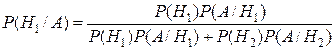 .
.
Действительно,
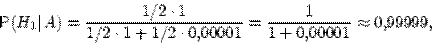
11.10. Два из трех независимо работающих элементов вычислительного устройства отказали. Найти вероятность того, что отказали первый и второй элементы, если вероятности отказа первого, второго и третьего элементов соответственно равны 0, 2; 0, 4 и 0, 3.
Решение. Обозначим.через А событие—отказали два элемента.
Можно сделать следующие предположения (гипотезы):
B1—отказали первый и второй элементы, а третий элемент
исправен, причем (поскольку элементы работают независимо, то применима теорема умножения)
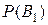 = p1 p2 q3= 0.2 0.4.0, 7 = 0, 056;
= p1 p2 q3= 0.2 0.4.0, 7 = 0, 056;
В2—отказали первый и третий элементы, а второй элемент исправен, причем
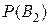 = p1 q2 p3==0, 2.0, 3 0, б = 0, 036;
= p1 q2 p3==0, 2.0, 3 0, б = 0, 036;
B3—отказали второй и третий элементы, а первый — исправен, причем
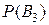 = q1 p2 p3= 0, 4.0, 3 0, 8 = 0, 096;
= q1 p2 p3= 0, 4.0, 3 0, 8 = 0, 096;
B4 — отказал только один элемент, В5 — отказали все три элемента, B6 — ни один из элементов не отказал.
Вероятности последних трех гипотез не вычислены, так как при этих гипотезах событие А (отказали два элемента) невозможно и значит условные вероятности 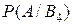 ,
, 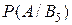 ,
, 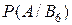 равны нулю.
равны нулю.
Поскольку при гипотезах В1 В2 В3, событие А достоверно, то соответствующие условные вероятности равны единице:
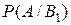 =
= 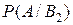 =
= 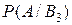 =1.
=1.
По формуле полной вероятности, вероятность того, что отказали два элемента,
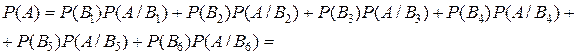
= 0, 056.1 + 0, 036.1 + 0, 096.1 = 0, 188.
По формуле Бейеса, искомая вероятность того, что отказали первый и второй элементы,
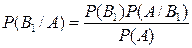 =
= 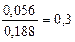 .
.
11.11. Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть две партии из четырех или три партии из шести (ничьи во внимание не принимаются)?
Решение. Играют равносильные шахматисты, поэтому вероятность выигрыша р = 1/2; следовательно, вероятность проигрыша q также равна 1/2. Так как во всех партиях вероятность выигрыша постоянна и безразлично, в какой последовательности будут выиграны партии, то применима формула Бернулли.
Найдем вероятность того, что две партии из четырех будут выиграны:
P4 (2)= 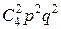 = 4*3/(1*2)*(1/2)2*(1/2)2 = 6/16.
= 4*3/(1*2)*(1/2)2*(1/2)2 = 6/16.
Найдем вероятность того, что будут выиграны три партии из шести:
P6 (3)= 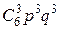 = 6*5*4/(1*2*3)*(1/2)3*(1/2)3 =5/16.
= 6*5*4/(1*2*3)*(1/2)3*(1/2)3 =5/16.
Так как P4 (2)> P6 (3), то вероятнее выиграть две партии из четырех, чем три из шести.
11.12. Найти вероятность того, что событие А наступит ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равна 0, 25.
Решение. По условию, n=243; k=70; р=0, 25; q=0, 75.
Так как n=243—достаточно большое число, воспользуемся локальной теоремой Лапласа:
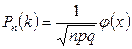 , где
, где 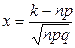
Найдем значение х:

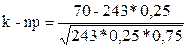 =1, 37/
=1, 37/
По таблице приложения 1 найдем 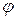 (1, 37) =0, 1561. Искомая вероятность
(1, 37) =0, 1561. Искомая вероятность
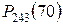 = (1/6, 75)*0, 1561 =0, 0231.
= (1/6, 75)*0, 1561 =0, 0231.
11.13 Вероятность появления события в каждом из 100 независимых испытаний постоянна и равна p = 0, 8. Найти вероятность того, что событие появится: а) не менее 75 раз и не более 90 раз; б) не менее 75 раз; в) не более 74 раз.
Решение. Воспользуемся интегральной теоремой Лапласа:
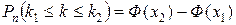 где Ф(x)—функция Лапласа,
где Ф(x)—функция Лапласа,
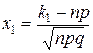 ,
, 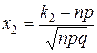
а) По условию, n= 100; р=0, 8; q=0, 2; k1 =75; k2=90. Вычислим х2 и х1:
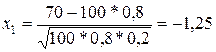 ,
, 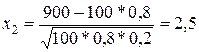
Учитывая, что функция Лапласа нечетна, т. е. Ф (—х) = —Ф (x) получим
P1oo(75  90)=Ф(2, 5)~Ф(~1, 25)=Ф(2, 5) + Ф(1, 25).
90)=Ф(2, 5)~Ф(~1, 25)=Ф(2, 5) + Ф(1, 25).
По таблице приложения 2 найдем:
Ф (2, 5) =0, 4938; Ф (1, 25) = 0, 3944.
Искомая вероятность
P1oo(75  90)=0, 4938+ 0, 3944 = 0, 8882.
90)=0, 4938+ 0, 3944 = 0, 8882.
б) Требование, чтобы событие появилось не менее 75 раз, означает, что число появлений события может быть равно 75 либо 76,..., либо 100. Таким образом, в рассматриваемом случае следует принять k1 =75; k2=100. Тогда
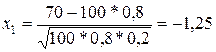 ,
, 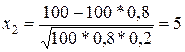
По таблице приложения 2 найдем Ф (1, 25) =0, 3944; Ф(5) = 0, 5.
Искомая вероятность
P1oo(75  100)==Ф (5)—Ф (— 1, 25) =Ф (5) +Ф (1, 25) =
100)==Ф (5)—Ф (— 1, 25) =Ф (5) +Ф (1, 25) =
= 0, 5 + 0, 3944 = 0, 8944.
в) События—«A появилось не менее 75 раз» и «A появилось не более 74 раз» противоположны, поэтому сумма вероятностей этих событий равна единице. Следовательно, искомая вероятность
P100 (0; 74) = 1 —P100 (75; 100) = 1—0, 8944 =0, 1056.
11.14 Испытывается каждый из 15 элементов некоторого устройства. Вероятность того, что элемент выдержит испытание, равна 0, 9. Найти наивероятнейшее число элементов, которые выдержат испытание.
Решение. По условию, n = 15, р=0, 9, q=0, 1. Найдем наивероятнейшее число mо из двойного неравенства np-q< mo < nр + р.
Подставив данные задачи, получим
150, 9—0, l< mo < 15-0, 9+0, 9, или 13, 5< mo < 14, 4.
Так как mo —целое число и поскольку между числами 13, 4 и 14, 4 заключено одно целое число, а именно 14, то искомое наивероятнейшее число ==14.
|
|