Унимодальное

.

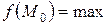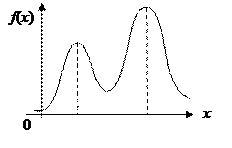Распределения могут быть:

· полимодальные

(бимодальное)

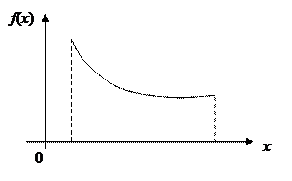· антимодальные

·

(амодальное)

2) Медиана и квартили случайных величин

Будем рассматривать непрерывные случайные величины. Квантилем порядка р называется корень уравнения

,

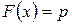где 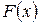– функция распределения.

При 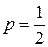получаем медиану. Обозначается .

.

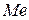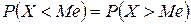Таким образом, это значение случайной величины такое, что вероятность того, что случайная величина примет значение больше или меньше 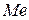, одинакова.

3) Математическое ожидание случайной величины

Рассмотрим дискретную случайную величину. Пусть произведено 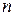опытов, в которых 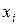наблюдалось 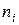раз. Тогда статическое среднее (среднее арифметическое по всем наблюдениям) вычисляется по формуле

.

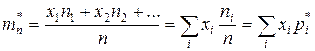При 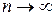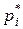приближается к , тогда 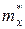приближается к величине

,

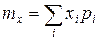которая называется математическим ожиданием дискретной случайной величины.

Математическое ожидание называют еще центром рассеивания случайной величины.

Другие обозначения:

, .

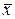Таким образом, при увеличении числа опытов среднее арифметическое значение случайной величины 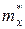будет приближаться к математическому ожиданию.

Эта связь между средним арифметическим и математическим ожиданием составляет содержание одной из форм закона больших чисел. Все формы закона больших чисел констатируют факт устойчивости некоторых средних при большом числе опытов. Сейчас речь идет об устойчивости среднего арифметического из ряда наблюдений одной и той же величины. При небольшом числе опытов среднее арифметическое их результатов случайно, при достаточном увеличении числа опытов оно становится «почти не случайным» и, стабилизируясь, приближается к постоянной величине – математическому ожиданию.

Например, многократное взвешивание с вычислением среднего арифметического.

При формальном (аксиоматическом) построении теории вероятностей доказываются следующие теоремы, выражающие закон больших чисел.

а) Теорема Чебышева

.

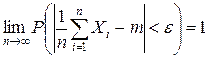
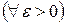б) Теорема Бернулли

,

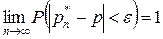
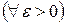где 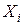– случайная величина, отвечающая наблюдению 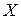в i -ом опыте,

т – математическое ожидание случайной величины.

Для непрерывной случайной величины математическое ожидание вводится путем предельного перехода.

Пусть дана непрерывная случайная величина 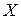, введем аппроксимирующую ее дискретную случайную величину 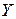со значениями 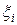, которым отвечают вероятности.

,

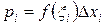где 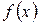– плотность распределения.

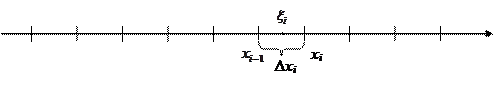Тогда

.

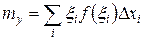Переходим к пределу при 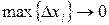. При этом функция распределения дискретной случайной величины 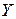сходится к функции распределения непрерывной случайной величины .

,

–

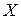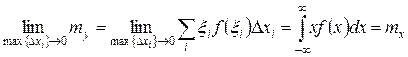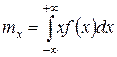математическое ожидание непрерывной случайной величины .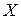

Опираясь на формулы для математического ожидания нетрудно показать справедливость следующих свойств.

1с) ;

2с) ;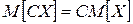

3с) ;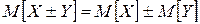

4с) ,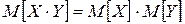

Х и Y – независимые случайные величины.

4) Дисперсия и среднее квадратическое отклонение случайной величины

Мода, медиана, математическое ожидание характеризуют положение случайной величины, но не характеризуют рассеивание.

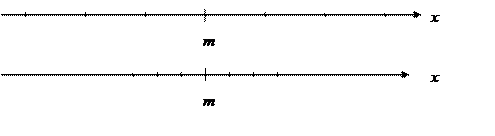Для характеристики рассеивания нужно рассматривать отклонение

.

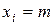Пусть имеем 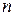опытов для дискретной случайной величины, причем 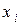появилось 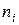раз. Рассмотрим среднее квадратическое значение для отклонений от центра рассеивания.

,

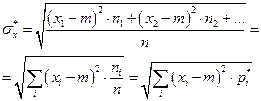при 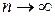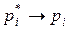и тогда .

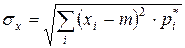
– среднее квадратическое отклонение случайной величины .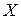

Величина

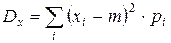– дисперсия случайной величины .

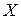– связь между средним квадратическим отклонением и дисперсией.

Для непрерывной случайной величины по аналогии с математическим ожиданием имеем

.

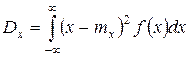Проанализировав формулы для дисперсии мы можем рассматривать ее как математическое ожидание случайной величины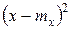

.

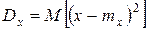Вводится понятие центрированной случайной величины

,

и тогда

,

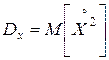т.е. дисперсия есть математическое ожидание квадрата центрированной случайной величины. Пользуются символами .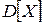

Опираясь на формулы для дисперсии, можно доказать такие свойства дисперсии.

1с) .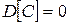

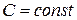2с) .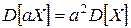

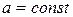3с)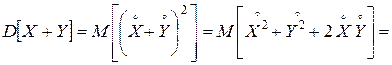

.

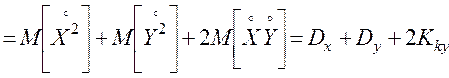Величину 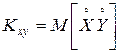называют корреляционным моментом случайных величин 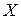и .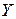

Для вычисления 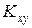по опытным данным используют формулу

.

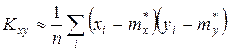Пары 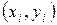наблюдались в 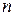опытах.

Если 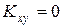, то случайные величины 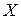и 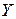называют некоррелированными.

5) Моменты случайной величины

Сам термин и способ построения заимствовал из механики (статические, центробежные моменты, моменты инерции).

Начальным моментом порядка 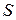называется число

.

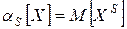Очевидно .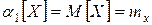

Центральным моментом порядка 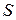называется число

.

,

.

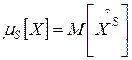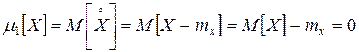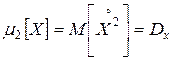Центральные моменты выражаются через начальные.

.

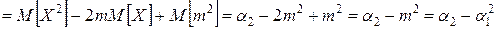Мы получили часто используемую формулу, связывающую дисперсию, начальный момент 2 ^го порядка и математическое ожидание.

.

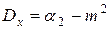– для дискретных случайных величин.

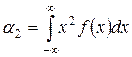– для непрерывных случайных величин.

Чем больше моментов мы рассматриваем, тем подробнее информация о случайной величине. Однако, надежно вычислить по опытным данным моменты высоких порядков бывает затруднительно. Поэтому в практических задачах моменты выше четвертого порядка не рассматриваются.

Важным является центральный момент 3 ^го порядка.

,

.

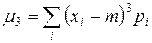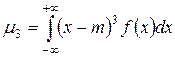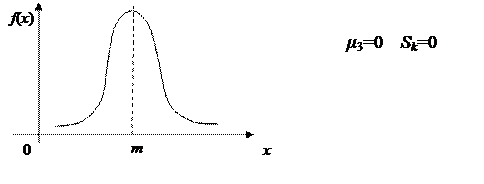Он характеризует асимметрию плотности вероятности.

Но величина 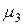размерная и поэтому «чувствительна к изменению масштаба» (в том числе и к рассеиванию).

Поэтому вводят безразмерную величину коэффициент асимметрии

.

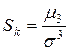Точно также вместо 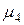вводят величину, называемую эксцессом

.

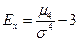Эксцесс характеризует остроконечность распределения по отношению к нормальному закону.

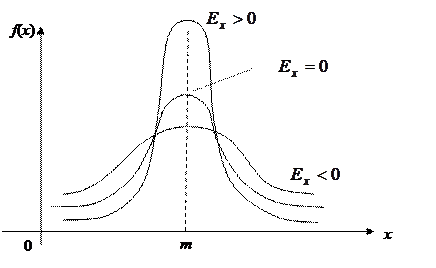Пример 1. Найти дисперсию случайной величины 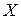, если дан ряд распределения.

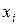
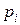
	0, 3	0, 5	0, 2

Решение. 1) Найдем математическое ожидание:

.

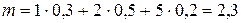2) Найдем все возможные значения квадрата отклонения:

,

,

.

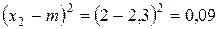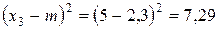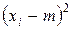
	1, 69	0, 09	7, 29
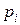
	0, 3	0, 5	0, 2

.
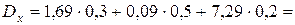
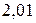