Регрессионный анализ. После того как с помощью корреляционного анализа выявлено наличие статистически значимых связей между переменными и оценена степень их тесноты

После того как с помощью корреляционного анализа выявлено наличие статистически значимых связей между переменными и оценена степень их тесноты, обычно переходят к математическому описанию конкретного вида зависимостей с использованием регрессионного анализа. С этой целью подбирают класс функций, связывающий результативный показатель 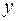и аргументы 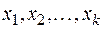, отбирают наиболее информативные аргументы, вычисляют оценки неизвестных значений параметров уравнения связи и анализируют точность полученного уравнения.

Функция регрессии – функция , описывающая зависимость условного среднего значения результативного признака 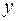от заданных значений аргументов.

Уравнение регрессии показывает ожидаемое значение зависимой переменной 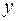при определенных значениях независимых переменных .

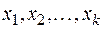По количеству включенных в модель факторов модели делятся на однофакторные (парная модель регрессия) и многофакторные (модель множественной регрессии), а по виду функции - на линейные и нелинейные.

Модель множественной линейной регрессии имеет вид

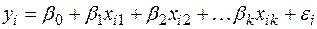, (1)

где 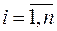, 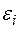- взаимно некоррелированные случайные величины с .

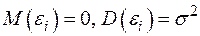Коэффициент регрессии показывает, на какую величину в среднем изменится результативный признак 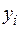, если увеличить на одну единицу измерения при фиксированных значениях остальных переменных, входящих в модель, т.е. является нормативным коэффициентом.

Для упрощения вычисления коэффициентов регрессии уравнение регрессии записывают в матричном виде:

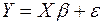, (2)

где - вектор-столбец наблюдений,

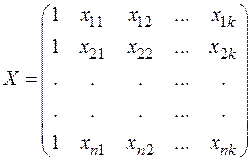- матрица наблюдений независимых переменных,

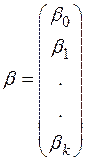- вектор-столбец неизвестных параметров, которые подлежат оцениванию,

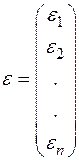- вектор-столбец случайных «ошибок».

Уравнение (2) содержит значения неизвестных параметров 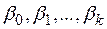. Эти величины оцениваются на основе выборочных наблюдений, поэтому полученные расчетные показатели не являются истинными, а представляют собой лишь их статистические оценки. Модель линейной регрессии, в которой вместо истинных значений параметров подставлены их оценки, имеет вид

, (3)

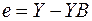- вектор «оцененных» отклонений регрессии, остатки регрессии,

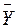- оценка значений 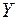, равная .

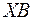Построение уравнения регрессии осуществляется с помощью метода наименьших квадратов, суть которого заключается в минимизации сумм квадратов отклонений фактических значений результативного признака от его расчетных значений, т.е.

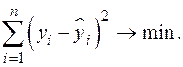
Формулу для вычисления параметров регрессионного уравнения по методу наименьших квадратов приведем без вывода:

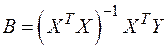. (4)

Для того чтобы регрессионный анализ, основанный на обычном методе наименьших квадратов, давал наилучшие из всех возможных результаты, должны выполнятся следующие условия, известные как условия Гаусса-Маркова.

1. Математическое ожидание случайной составляющей в любом наблюдении должно быть равно нулю;

2. Дисперсия случайной составляющей должна быть постоянна для всех наблюдений;

3. Отсутствие систематической связи между значениями случайной составляющей в любых двух наблюдениях;

4. 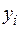есть величина случайная, а 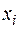- неслучайная.

Качество модели регрессии связывают с адекватностью модели наблюдаемым данным. Проверка адекватности модели регрессии наблюдаемым данным проводится на основе анализа остатков .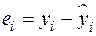

При анализе качества модели регрессии в первую очередь используют коэффициент детерминации

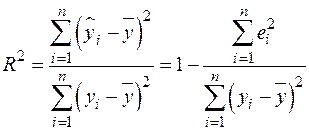, (5)

где 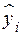- предсказанное значение зависимой переменной;

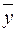- среднее значение зависимой переменной.

Чем ближе 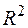к единице, тем выше качество модели.

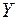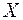Важным моментом является проверка значимости построенного уравнения в целом и отдельных параметров. Оценить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между и , фактическим данным и достаточно ли включенных в уравнение объясняющих переменных 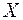для описания зависимой переменной .

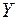Оценка значимости уравнения регрессии проводится для того, чтобы узнать, пригодно уравнение регрессии для практического использования или нет.

Для проверки значимости модели регрессии используют F-критерий Фишера:

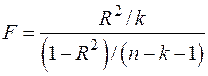. (7)

Если расчетное значение с 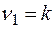и 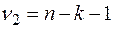степенями свободы, где k – количество факторов, включенных в модель, больше табличного при заданном уровне значимости, то модель считается значимой.

В качестве меры точности применяют несмещенную оценку дисперсии остаточной компоненты, которая представляет собой отношение суммы квадратов уровней остаточной компоненты к величине 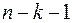. Квадратный корень из этой величины называется стандартной ошибкой:

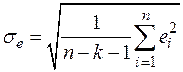. (8)

Значимость отдельных коэффициентов регрессии проверяется по t -статистике путем проверки гипотезы о равенстве нулю j -го параметра уравнения (кроме свободного члена):

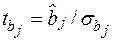, (9)

- стандартное отклонение коэффициента уравнения регрессии .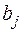

Величина представляет собой квадратный корень из произведения несмещенной оценки дисперсии 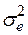и j -го диагонального элемента матрицы, обратной матрице :

,

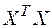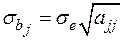где 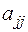- диагональный элемент матрицы .

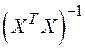Если расчетное значение t -критерия с 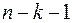степенями свободы превосходит его табличное значение при заданном уровне значимости, коэффициент регрессии считается значимым. В противном случае фактор, соответствующий этому коэффициенту, исключают из модели.

Прогноз, полученный подстановкой в уравнение регрессии ожидаемого значения параметра, является точечным. Вероятность реализации такого прогноза ничтожно мала. Целесообразно определить доверительный интервал прогноза.

Для линейной модели регрессии при прогнозировании индивидуальных значений границы доверительного интервала рассчитываются по формуле 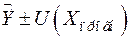. Величина отклонения от линии регрессии 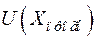вычисляется по формуле

, (10)

где ;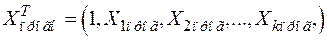

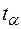- табличное значение t статистики Стъюдента при заданном уровне значимости .

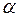Одним из условий регрессионной модели является предположение о линейной независимости объясняющих переменных, т.е. решение задачи возможно лишь тогда, когда столбцы и строки матрицы исходных данных линейно независимы.

Под мультиколлинеарностью понимается высокая взаимная коррелированность объясняющих переменных, которая приводит к линейной зависимости нормальных уравнений.

Существуют различные способы для определения наличия или отсутствия мультиколлинеарности:

· анализ матрицы коэффициентов парной корреляции. Явление мультиколлинеарности в исходных данных считают установленным, если коэффициент парной корреляции между двумя переменными больше 0, 8;

· исследование матрицы 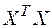. Если определитель матрицы 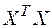близок к нулю, это свидетельствует о наличии мультиколлинеарности.

Для устранения или уменьшения мультиколлинеарности используется ряд методов:

· исключение одного из двух сильно связанных факторов. Это самый простой, но не всегда самый эффективный метод. Он состоит в том, что из двух объясняющих переменных, имеющих высокий коэффициент корреляции одну переменную исключают из рассмотрения. Оставляют ту, которая имеет больший коэффициент корреляции с зависимой переменной;

· переход от первоначальных факторов к их главным компонентам, число которых может быть меньше, затем возвращение к первоначальным факторам;

· использование стратегии шагового отбора, реализованный в ряде алгоритмов пошаговой регрессии.

Наиболее широкое применение получили следующие схемы построения уравнения множественной регрессии:

· метод включения факторов;

· метод исключения – отсев факторов из полного его набора.

В соответствии с первой схемой признак включается в уравнение в том случае, если его включение существенно увеличивает значение коэффициента множественной корреляции, что позволяет последовательно отбирать факторы, оказывающие существенное влияние на результирующий признак даже в условиях мультиколлинеарности системы признаков, отобранных в качестве аргументов из содержательных соображений. При этом первым в уравнение включается фактор, наиболее тесно коррелирующий с 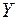, вторым – тот фактор, который в паре с первым из отобранных дает максимальное значение коэффициента множественной корреляции, и т.д. существенно, что на каждом шаге получают новое значение коэффициента множественной корреляции (большее, чем на предыдущем шаге); тем самым определяется вклад каждого отобранного фактора в объясненную дисперсию .

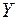Вторая схема пошаговой регрессии основана на последовательном исключении факторов с помощью t -критерия. Она заключается в том, что после построения уравнения регрессии и оценки значимости всех коэффициентов регрессии из модели исключают тот фактор, коэффициент при котором незначим и имеет наименьшее значение t -статистики по абсолютной величине. После этого получают новое уравнение множественной регрессии и снова проводят оценку значимости вснх оставшихся коэффициентов регрессии. Если и среди них окажутся незначимые, то опять исключают фактор с наименьшим значением t -критерия. Процесс исключения факторов останавливается на том шаге, при котором все регрессионные коэффициенты значимы.

При отборе факторов также рекомендуется пользоваться следующим правилом: число включаемых факторов обычно в 6-7 раз меньше объема совокупности, по которой строится регрессия. Если это соотношение нарушено, то число степеней свободы остаточной дисперсии очень мало. Это приводит к тому, что параметры уравнения регрессии оказываются статистически незначимыми, а F -критерий меньше табличного.

Пример.