Метод наименьших квадратов для функции нескольких переменных

Будем теперь считать, что исследуемая величина у связана некоторым образом с величинами х₁, х_2, …, х_k - входными величинами (факторами), значения каждого из которых могут быть выбраны произвольно из некоторой области.

Пусть связь у с х₁, х₂,..., х_k характеризуется зависимостью (видом регрессии у на х₁, х₂,..., х_k).

(4.39)

Функцию 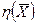называют функцией отклика. Эта функция обычно неизвестна экспериментатору, но, обладая некоторой информацией или интуицией, экспериментатор выбирает вид этой функции. Будем брать эту функцию в виде линейно зависящей от нескольких числовых параметров θ ₁, θ ₂, …, θ _m.

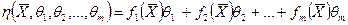(4.40)

Вид функции f_i 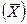- известен. Обозначим

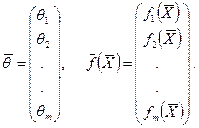(4.41)

В векторных обозначениях выражение (4.40) можно записать:

(4.42)

Чтобы получить математическую модель процесса, нужно определить вектор θ в (4.42) (оценить 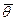и оценки найти наилучшие в некотором смысле). Доказано, что наилучшие линейные оценки 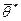, полученные для 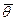, дает метод наименьших квадратов. В выражении (4.42) вектор 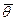входит как раз линейно. Есть и другие способы оценки 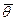. Заметим, что эти оценки должны быть состоятельными, несмещенными и обладать наименьшими дисперсиями среди всех оценок 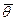. Такие оценки и называются наилучшими линейными оценками.

Предположим, что в точках 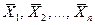(n - разных наборов факторов факторного пространства были проведены независимые измерения y₁, y₂, …, y_n с дисперсиями σ ²₁, σ ²_{1, …,} σ ²_n. В дальнейшем будем считать, что y₁ - это среднее выборочное значение, а среди 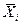нет одинаковых.

Нам нужно построить оценку параметров 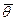. Известно, что наилучшая линейная оценка 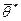минимизирует сумму взвешенных квадратичных отклонений.

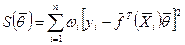(4.43)

где .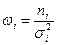

Условия минимума для (4.43) имеют вид

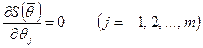. (4.44)

Откуда, решив систему линейных алгебраических уравнений (4.44), найдем 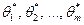- оценки для θ ₁, θ ₂, …, θ _m. Подставляя эти значения в (4.42), найдем аналитическую зависимость у от х₁, х₂,..., x_k, т. е. математическую модель исследуемого экспериментально процесса.