
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Математическая модель эксперимента. Метод наименьших квадратов
|
|
После того как проведены первичная статистическая обработка результатов эксперимента и обоснование точности полученных экспериментальных данных необходимо найти аналитическую зависимость выходного параметра y от входных параметров (факторов) x1, x2, …, xk.
Рассмотрим простейший случай. Пусть выходной параметр y зависит только от одного фактора x. В результате проведения эксперимента получим данные, представленные в таблице 3.
Таблица 3 – Результаты эксперимента
| Параметры | Значения | |||
| x | x1 | x2 | … | xm |
| y | у1 | y2 | … | ym |
Возникает задача найти функцию y = f(x), отражающую в основном характер экспериментальной зависимости, - это задача сглаживания экспериментальной зависимости. Так как y и x случайные величины, то кривая, проходящая через точки Мi (рисунок 10), не отражает основного характера зависимости y = f(x). Кривой, отражающей в основном характер экспериментальной зависимости у = f(х), будет кривая Г.
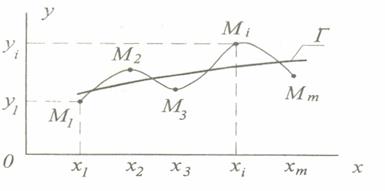
Рисунок 10 – Сглаживание экспериментальной зависимости
Решают две вспомогательные задачи.
1 Определение вида сглаживающей функции.
2 Определение значений параметров, входящих в сглаживающую функцию [17].
Первая задача решается исходя из дополнительной информации об эксперименте, вторая - математическими методами. Зачастую сглаживающая функция представляется в виде линейной комбинации неизвестных числовых параметров и некоторых известных линейно независимых функций
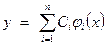 (4.14)
(4.14)
Такими функциями, например, могут быть
 (4.15)
(4.15)
Для удобства дальнейших вычислений вводят в эту матрицу еще одну переменную, она называется «фиктивной» и во всех опытах равна x0u = +1. В результате получена матрица размерностью N*(K+1). Вектор наблюдений образует другую матрицу, размерностью N*1.
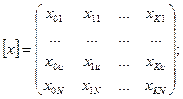
 . (4.16)
. (4.16)
Рассмотрим на примере однофакторной модели идею метода наименьших квадратов, который дает наилучшие линейные оценки.
Для однофакторной модели (линейной) матрица 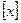 содержит лишь два столбца. Необходимо подобрать такие значения b0 и b1 (или так провести прямую на графике (рисунок 11) в координатах X1 и Y), чтобы модель наилучшим образом удовлетворяла данным. Провести прямую через все точки с координатами (X1u и Yu) практически невозможно. Это объясняется тем, что:
содержит лишь два столбца. Необходимо подобрать такие значения b0 и b1 (или так провести прямую на графике (рисунок 11) в координатах X1 и Y), чтобы модель наилучшим образом удовлетворяла данным. Провести прямую через все точки с координатами (X1u и Yu) практически невозможно. Это объясняется тем, что:
а) измерения Yu точны, но гипотеза о линейном влиянии X1 на Y не соответствует истине;
б) влияние X1 на Y действительно линейно, но Yu измерено со значительной среднеквадратической ошибкой Sэ;
 |
Рисунок 11 – Графическое изображение однофакторной модели
y=b0x0 + b1x1
в) одновременно несовершенна гипотеза линейности и существует ошибка измерения Sэ.
Следовательно, всегда между наблюдаемыми значениями (Yu) и расчетными значениями (Ŷ u) возможна разница (∆ u):
∆ u =Yu - Ŷ u (4.17)
Необходимо свести общую разницу к минимуму. При этом наименее громоздкие вычисления получаются, если минимизировать не сумму абсолютных отклонений по всем опытам,  , а сумму квадратов отклонений:
, а сумму квадратов отклонений:
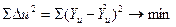 (4.18)
(4.18)
При подстановке значений Ŷ u из модели для каждого опыта получим:
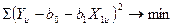 (4.19)
(4.19)
Для нахождения минимума функции необходимо приравнять к нулю частные производные по всем неизвестным, т.е. по b0 и b1. Получаем систему нормальных уравнений, при решении которых и будут вычислены неизвестные коэффициенты модели:
 (4.20)
(4.20)
сокращая оба уравнения на «-2» и производя почленное суммирование, получим:
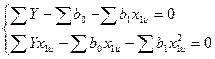 (4.21)
(4.21)
Далее вводим обозначения:
N(u)=(00) Σ X1u=(01) Σ Y=(0Y)
Σ X1u=(10) Σ X1u2=(11) Σ YX1u=(1Y)
Тогда система уравнений примет вид:
 (4.22)
(4.22)
Неизвестные оценки коэффициентов модели образуют вектор b:
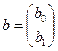
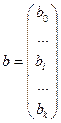 (4.23)
(4.23)
Известные априори суммы (00), (i0), (ij) и (ii), определенные только уровнями факторов Xi в информационной таблице, образуют квадратичную матрицу М размером (k+1)*(k+1):
М = 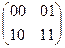
 (4.24)
(4.24)
Эта матрица называется матрицей моментов плана, ее можно получить из матрицы плана X1, если последнюю умножить слева на транспонированную матрицу XТ: М= XТ* X.
С целью исследования свойств и обобщения результатов для матриц различных планов X матрицу М целесообразно нормировать по числу опытов, получая информационную матрицу MN= 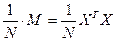 .
.
Известные апостериори суммы (0Y) и (iY), включающие результаты эксперимента, образуют вектор YM, являющийся произведением XТ на вектор наблюдений Y:

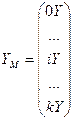 YM=XТY (4.25)
YM=XТY (4.25)
Следовательно, в матричной форме система нормальных уравнений записывается:
Мb= УМ (4.26)
А с учетом матрицы Х: ХТХВ= ХТУ из нее определяется вектор оценок коэффициентов:
b = М-1УМ = (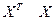 )-1ХТУ = N-1MN-1XTY = ДХТY = LY (4.27)
)-1ХТУ = N-1MN-1XTY = ДХТY = LY (4.27)
В данном случае выделены две новые независимые от результатов эксперимента матрицы: так называемая D -матрица, или ковариационная, элементы которой оценивают статистические характеристики модели, и так называемая L- матрица, элементы которой позволяют рассчитывать оценки bi без обращения матриц по простым формулам с помощью микрокалькуляторов.
Д = М-1 = (ХТХ)-1 (4.28)
L = DХТ = (ХТХ)-1ХТ (4.29)
Неизвестные оценки в системе нормальных уравнений можно рассчитать через определитель det M = A матрицы моментов и определителя det Mi = Ai матриц Mi, образуемых путем замены i-го столбца на вектор-столбец УМ:
bi = det Mi/ det M = Ai/A (4.30)
Таким образом, для однофакторной модели при использовании правила Крамера используются простые формулы:
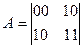
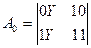
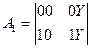
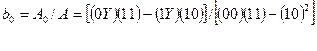 (4.31)
(4.31)
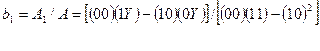
Ковариационная матрица D = ХТХ-1 определяется только матрицей независимых переменных Х, т.е. планом эксперимента, поэтому априорный анализ ее свойств лежит в основе синтеза этих планов [7]. Точность оценивания параметров модели зависит от матрицы М или другими словами от выбора точек Хij. Это даёт возможность ставить задачу об оптимальном выборе точек, то есть планировании экспериамента. Набор координат этих точек называют планом эксперимента.
Рассмотрим пример. Найти функцию, отражающую экспериментальную зависимость у от x, используя данные таблицы 4.
Таблица 4 – Результаты эксперимента
| Параметры | Значения параметров | |||||||||
| x | 1, 20 | 1, 31 | 1, 40 | 1, 61 | 1, 74 | 1, 80 | 2, 00 | 2, 14 | 2, 19 | 2, 41 |
| y | 0, 54 | 0, 59 | 0, 67 | 0, 76 | 0, 85 | 0, 97 | 1, 07 | 1, 18 | 1, 27 | 1, 30 |
Функцию у = f(х) возьмем в виде
y = C1x2 + C2x + C3.
Неизвестные С1, С2, С3 определим из условий (4.15).
Здесь φ 1(х) = x2, φ 2(х) = х, φ 3(х) = 1.
В результате получим систему
128, 94 С1 + 64, 30 С2 + 33, 17 С3 = 34, 63;
64, 30 С1 + 33, 17 С2 + 17, 80 С3 = 17, 60;
33, 17 С1 + 17, 80 С2 + 10, 00 С3 = 9, 29.
Решив эту систему, найдем С1 = 0, 168; С2 = 0, 102; С3 = 0, 189.
Следовательно, функциональная зависимость у от х имеет вид
у = 0, 168 х2 + 0, 102 х + 0, 189.
|
|