
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Предел числовой последовательности
|
|
СПРАВОЧНЫЕ СВЕДЕНИЯ
2.1 Определение предела числовой последовательности
Число 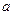 называют пределом последовательности
называют пределом последовательности  , если для каждого
, если для каждого 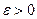 существует такое натуральное число
существует такое натуральное число 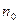 , что для любого
, что для любого 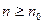 верно неравенство:
верно неравенство:
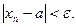
Используя логические символы данное определение можно записать в следующем виде:
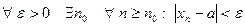 .
.
На «языке окрестностей» определение звучит так: число 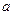 называют пределом последовательности
называют пределом последовательности  , если для каждой окрестности точки
, если для каждой окрестности точки 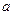 (т.е. точки, координата которой равна а) найдется номер, начиная с которого все члены последовательности принадлежат этой окрестности. Используя логические символы определение можно записать в следующем виде:
(т.е. точки, координата которой равна а) найдется номер, начиная с которого все члены последовательности принадлежат этой окрестности. Используя логические символы определение можно записать в следующем виде:
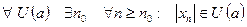 .
.
Иными словами, какую бы окрестность точки 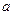 ни взять, вне этой окрестности находится лишь конечное количество членов рассматриваемой последовательности (либо нет ни одного члена данной последовательности).
ни взять, вне этой окрестности находится лишь конечное количество членов рассматриваемой последовательности (либо нет ни одного члена данной последовательности).
Если 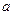 — предел последовательности
— предел последовательности  , то пишут
, то пишут
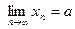 ,
,
а саму последовательность называют сходящейся.
Сходящаяся последовательность может иметь только один предел.
Число 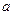 не является пределом последовательности
не является пределом последовательности  (
(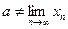 ), если существует такое число
), если существует такое число 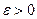 , что для любого натурального
, что для любого натурального 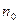 найдется номер
найдется номер 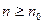 такой, что
такой, что
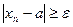 ,
,
другими словами
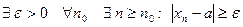 ;
;
или, 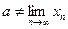 , если существует такая окрестность точки
, если существует такая окрестность точки 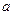 , вне которой находится бесконечно много членов последовательности
, вне которой находится бесконечно много членов последовательности  .
.
Последовательность называют расходящейся, если никакое число не является ее пределом, другими словами, если для любого числа 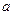 существует такое число
существует такое число 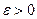 , что для любого натурального
, что для любого натурального 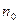 найдется номер
найдется номер 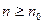 такой, что
такой, что
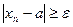 ,
,
или
 .
.
2.2 Свойства сходящихся последовательностей
1) Если последовательность сходится, то она ограниченна.
Значит, неограниченная последовательность будет расходящейся.
Последовательность, сходящуюся к нулю, называют бесконечно малой.
Если последовательность {хп} бесконечно малая, а последовательность {уп} ограниченная, то их произведение, т.е. последовательность {хпуп}, также является бесконечно малой.
2) Для того, чтобы число а было пределом последовательности {хп}, необходимо и достаточно, чтобы для всех п
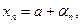
где {  } -- бесконечно малая последовательность.
} -- бесконечно малая последовательность.
3) Если существует 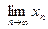 , то для любого числа
, то для любого числа  существует
существует
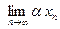 и
и 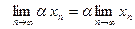 .
.
4) Если существуют 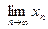 и
и 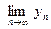 , то
, то
а) существует 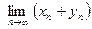 и
и
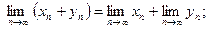
б) существует 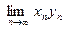 и
и
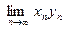 =
= 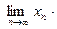
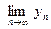
в) если к тому же 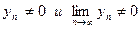 , то существует
, то существует 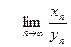 u
u
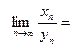
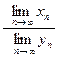
5) Если 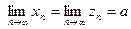 , и для всех n, начиная с некоторого,
, и для всех n, начиная с некоторого, 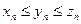 , то
, то
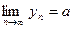 .
.
Это свойство еще называют леммой «о двух милиционерах».
6) Если 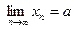 , и для всех п, начиная с некоторого,
, и для всех п, начиная с некоторого, 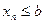 (или
(или 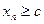 ), то
), то
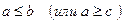 .
.
7) Если 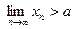 (или
(или 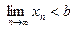 ), то для всех п, начиная с некоторого,
), то для всех п, начиная с некоторого,
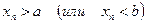 .
.
2.3 Бесконечно большие последовательности
Последовательность 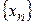 называют бесконечно большой, если для каждого
называют бесконечно большой, если для каждого 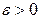 существует такое натуральное число
существует такое натуральное число 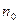 , что для любого
, что для любого 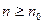 верно неравенство
верно неравенство
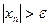 ,
,
и в этом случае пишут
 .
.
Бесконечно большая последовательность 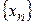 имеет пределом
имеет пределом 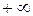 (соответственно
(соответственно 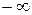 ), если для каждого
), если для каждого 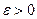 существует такое натуральное число
существует такое натуральное число 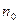 , что для любого
, что для любого 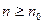 верно неравенство
верно неравенство
 (соответственно
(соответственно 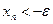 ).
).
Этот факт записывают так:
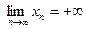 (соответственно
(соответственно  ).
).
Во всех этих случаях говорят, что последовательность имеет бесконечный предел.
Всякая бесконечно большая последовательность является неограниченной и расходящейся.
Неограниченная последовательность может и не быть бесконечно большой.
2.4 Частичный предел. Теорема Больцано-Вейерштрасса
Если подпоследовательность 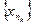 последовательности
последовательности 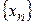 имеет предел
имеет предел 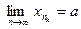 , где a — число или одна из бесконечностей
, где a — число или одна из бесконечностей 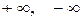 , то а называют частичным пределом последовательности
, то а называют частичным пределом последовательности  .
.
Если  , где а - число или одна из бесконечностей
, где а - число или одна из бесконечностей 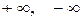 , то любая подпоследовательность
, то любая подпоследовательность 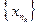 последовательности
последовательности 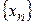 имеет тот же предел:
имеет тот же предел:
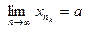 .
.
Теорема (Больцано-Вейерштрасса). Любая ограниченная последовательность содержит сходящуюся подпоследовательность.
Всякая неограниченная последовательность имеет частичный предел 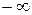 или
или 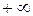 . Таким образом, множество частичных пределов любой последовательности не пусто.
. Таким образом, множество частичных пределов любой последовательности не пусто.
Пусть L - множество частичных пределов последовательности 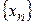 (наряду с числами L может содержать и
(наряду с числами L может содержать и 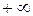 , и
, и 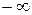 ). Верхним (нижним) пределом последовательности
). Верхним (нижним) пределом последовательности 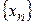 называют supL (inf L ), и обозначают его
называют supL (inf L ), и обозначают его
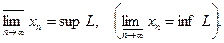
Верхний и нижний пределы последовательности являются ее частичными пределами.
2.5 Фундаментальные последовательности. Критерий Коши
Последовательность 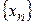 называют фундаментальной, если для каждого
называют фундаментальной, если для каждого 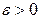 существует такое натуральное N, что для любого
существует такое натуральное N, что для любого 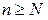 и любого
и любого 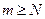 верно неравенство
верно неравенство
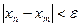 .
.
Используя логические символы определение можно записать в следующем виде:
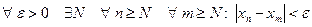
(условие Коши). Это же условие формулируют и так: для каждого 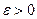 существует такое натуральное N, что для любого
существует такое натуральное N, что для любого 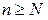 и любого натурального р верно неравенство:
и любого натурального р верно неравенство:
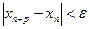 .
.
В символической записи определение выглядит так:
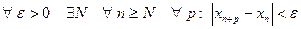 .
.
Теорема (критерий Коши). Для того, чтобы последовательность имела конечный предел, необходимо и достаточно, чтобы она была фундаментальной.
Для того, чтобы последовательность не имела конечного предела, необходимо и достаточно, чтобы она не удовлетворяла условию Коши, т.е. удовлетворяла отрицанию условия Коши: существует такое 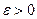 , что для любого натурального N найдутся такие
, что для любого натурального N найдутся такие 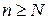 и
и  , что
, что
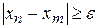 ,
,
или в символической записи:
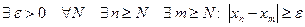 .
.
2.6 Монотонные последовательности. Число е
Теорема (Вейерштрасса). Ограниченная и монотонная, начиная с некоторого номера, последовательность имеет конечный предел.
Последовательность
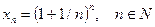 ,
,
строго возрастает (т.е. 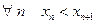 ) иограничена (
) иограничена (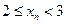 ), поэтому имеет предел, обозначаемый е:
), поэтому имеет предел, обозначаемый е:
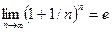 .
.
Иррациональное число е = 2, 718 281 828 459 045 …
ПРИМЕРЫ С РЕШЕНИЯМИ
Пример 1. Используя определение предела числовой последовательности, доказать, что число 1 является пределом последовательности 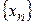 , где
, где 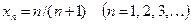 .
.
Решение. Рассмотрим модуль разности
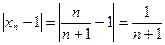 .
.
Возьмем произвольное число 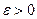 . Неравенство
. Неравенство 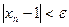 будет выполнено, если
будет выполнено, если 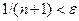 , т.е. при
, т.е. при 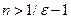 . В качестве
. В качестве 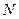 возьмем какое-нибудь натуральное число, удовлетворяющее условию
возьмем какое-нибудь натуральное число, удовлетворяющее условию 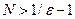 , тогда
, тогда 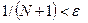 и для всех
и для всех 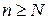 выполнены неравенства
выполнены неравенства
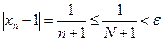 .
.
Это и означает, что 1 есть предел последовательности  , т. е.
, т. е.
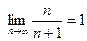 .
.
Пример 2. Используя определение предела числовой последовательности, доказать, что
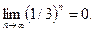
Решение. Так как 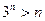 для любого
для любого 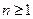 , то
, то
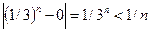 .
.
Пусть 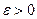 , выберем натуральное
, выберем натуральное 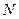 такое, что
такое, что 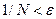 . Тогда для любого
. Тогда для любого 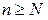 имеем
имеем
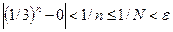 .
.
Значит, 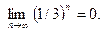
Пример 3. Используя определение предела числовой последовательности, доказать, что последовательность 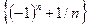 расходится.
расходится.
Решение. Нужно доказать, что никакое число не является пределом данной последовательности.
Докажем, что это действительно так для любых двух соседних членов. Из этих членов один имеет четный номер 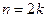 , и
, и
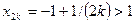 .
.
Соседний член имеет нечетный номер 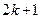 (или
(или 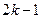 ), и
), и
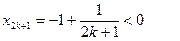 (или
(или 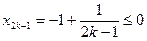 ).
).
Отсюда следует, что 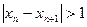 .
.
Для произвольного числа 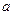 возьмем в качестве окрестности – интервал
возьмем в качестве окрестности – интервал 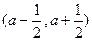 и путем несложных вычислений убедимся, что любые два соседних члена нашей последовательности
и путем несложных вычислений убедимся, что любые два соседних члена нашей последовательности 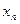 и
и 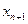 не могут одновременно принадлежать этой окрестности, так как всегда |
не могут одновременно принадлежать этой окрестности, так как всегда | 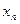 -
- 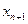 | > 1. Что и достаточно для доказательства расходимости рассматриваемой последовательности.
| > 1. Что и достаточно для доказательства расходимости рассматриваемой последовательности.
Пример 4. Доказать, что последовательность 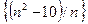 расходится.
расходится.
Решение. Докажем, что данная последовательность не ограничена. Имеем
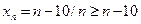 .
.
Пусть  – произвольное положительное число. Возьмем какое-нибудь натуральное число
– произвольное положительное число. Возьмем какое-нибудь натуральное число 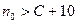 , тогда
, тогда 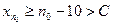 . Это означает, что последовательность
. Это означает, что последовательность 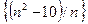 не ограничена, а поэтому расходится.
не ограничена, а поэтому расходится.
Пример 5. Найти 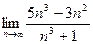 .
.
Решение. Преобразуем формулу общего члена последовательности:
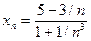 .
.
Учитывая, что 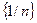 и
и 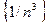 - бесконечно малые последовательности, и используя теоремы о пределах, получаем
- бесконечно малые последовательности, и используя теоремы о пределах, получаем
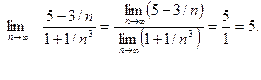
Пример 6. Доказать, что 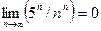 .
.
Решение. Для всех 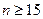 верно неравенство
верно неравенство 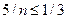 , поэтому
, поэтому
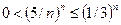
при 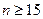 . Здесь слева и справа стоят члены последовательности, имеющие своим пределом нуль. Значит, по лемме «о двух милиционерах»
. Здесь слева и справа стоят члены последовательности, имеющие своим пределом нуль. Значит, по лемме «о двух милиционерах»
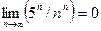 .
.
Пример 7. Найти 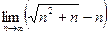 .
.
Решение. Преобразуем формулу общего члена последовательности:
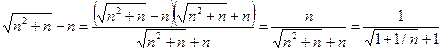 .
.
Поскольку 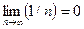 , то
, то
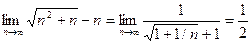 .
.
Пример 8. Для последовательности
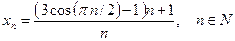 ,
,
найти множество частичных пределов 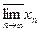 и
и 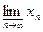 , а также
, а также 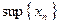 и
и 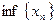 .
.
Решение. При 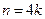 имеем
имеем
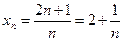 ,
,
и, значит, 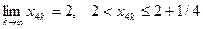 , причем
, причем 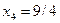 . При
. При 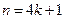 или
или 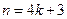 имеем
имеем
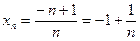 ,
,
И, значит, 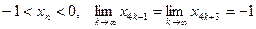 . При
. При 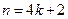 имеем
имеем
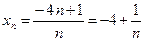 ,
,
значит, 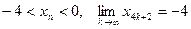 .
.
Таким образом, числа 2, -1, -4 являются частичными пределами данной последовательности. Рассмотренные четыре подпоследовательности 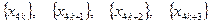 составляют вместе всю данную последовательность. Отсюда следует, что других частичных пределов последовательность не имеет.
составляют вместе всю данную последовательность. Отсюда следует, что других частичных пределов последовательность не имеет.
Очевидно,
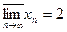 ,
, 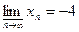 .
.
Из предыдущих рассмотрений следует также, что
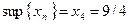 ,
, 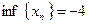 .
.
ЗАДАЧИ
Задача 1. Доказать, что 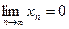 , указав для каждого
, указав для каждого 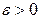 такое
такое 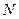 , что для любого
, что для любого 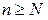 верно неравенство
верно неравенство 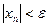 , если:
, если:
1) 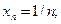 2)
2) 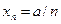 (а – произвольное данное число); 3)
(а – произвольное данное число); 3) 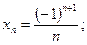
4) 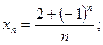 5)
5) 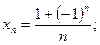 6)
6) 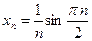 .
.
Задача 2. Доказать, что:
1) 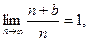 где
где 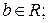 2)
2) 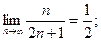 3)
3) 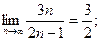
4) 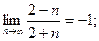 5)
5) 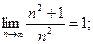 6)
6) 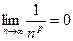 , где
, где 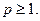
Задача 3. Доказать, что следующие последовательности являются бесконечно малыми:
1) 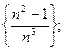 2)
2) 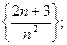 3)
3)  4)
4) 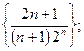 5)
5) 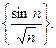
Задача 4. Доказать, что следующие последовательности являются расходящимися:
1) 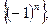 2)
2) 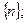 3)
3) 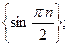 4)
4) 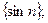 5)
5) 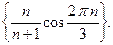
Задача 5. Найти 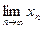 , если:
, если:
1) 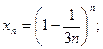 2)
2) 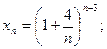 3)
3) 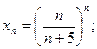
4) 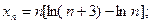 5)
5) 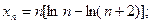 6)
6) 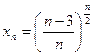
Задача 6. Найти 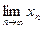 , если:
, если:
1) 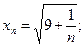 2)
2) 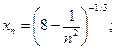 3)
3) 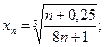
4) 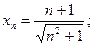 5)
5) 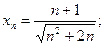 6)
6) 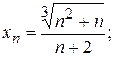
7) 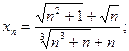 8)
8) 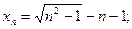 9)
9) 
10) 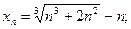 11)
11) 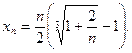
Задача 7. Найти 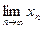 , если:
, если:
1) 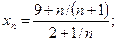 2)
2) 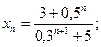 3)
3) 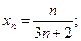
4) 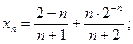 5)
5) 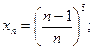 6)
6) 
7) 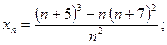 8)
8) 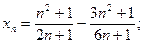 9)
9) 
10) 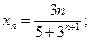 11)
11) 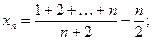 12)
12) 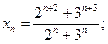
13) 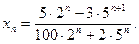
Задача 8. Найти 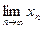 , если
, если 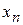 равно:
равно:
1) 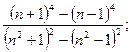 2)
2) 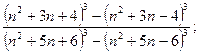
3) 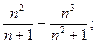 4)
4) 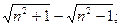 5)
5) 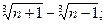
6) 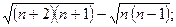 7)
7) 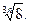
Задача 9. Доказать, что последовательности являются бесконечно большими:
1) 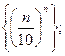 2)
2)  3)
3) 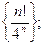 4)
4) 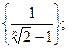 5)
5) 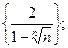
6)  7)
7) 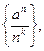 где
где 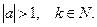
Задача 10. Найти все частичные пределы последовательностей:
1) 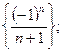 2)
2) 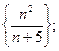 3)
3) 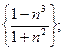 4)
4) 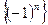 ;
;
5) 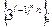 6)
6) 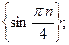 7)
7) 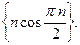
Задача 11. Найти 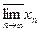 и
и 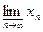 последовательностей:
последовательностей:
1) 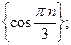 2)
2) 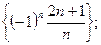 3)
3) 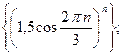
4) 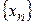
|
|